Методика решения нестандартных задач

1. Геометрические характеристики поперечных сечения брусьев

1.1. Вычисление моментов инерции относительно произвольных осей

1.1.1. Геометрические характеристики поперечных сечений брусьев, вычисленные относительно главных центральных осей, входят в расчетные формулы для определения напряжений и перемещений в брусьях. Без знания этих характеристик невозможно оценить прочность жёсткость и устойчивость брусьев.

Между моментами инерции поперечных сечений относительно центральных осей x0 , y0 , параллельных им осей x, у и наклонённых к последним под углом α

1.1.3. В некоторых случаях при определении момента инерции удобно достроить заданное сечение до такой фигуры, для которой величина осевого момента инерции известна (рис.1.3, а). Из рис. 1.3, а очевидно:

2

J x J x ABD J x ACD

Задача 1.3. Для сечений, указанных на рис.1.3, б-г, вычислить момент инерции относительно оси x.

Указание. Дополнить сечения на рис.1.3, б-г соответственно до параллелограмма, двух квадратов, кольца.

1.2.Главные оси и главные моменты инерции сечения

1.2.1.В теории геометрических характеристик широко используются формулы для определения направления главных осей и вычисления главных моментов инерции по известным осевым и центробежному моментам инерции относительно произвольных исходных осей х, у (рис.1.1, б):

Задача 1.4, Для сечений на рис.1.1, в-е найти положение главных осей инерции, проходящих через точку А, и величину главных моментов инерции.

Указание. Моменты инерции относительно осей х, у ( Jx, Jу, Jxу ) взять из задачи 1.1.

1.2.2. Основной признак главных осей - равенство пулю центробежного момента инерции относительно этих осой:

Если сечение состоит из двух одинаковых фигур, расположенных под углом 90˚, то одна главная центральная ось проходит через центры тяжести обеих фигур, а другая – перпендикулярно ей через центр тяжести сечения С

(рис.I.5, а)..

Задача 1.5. Указать положение главных центральных осей инерции и ту из них в каждом сечении (рис.1.5, б-г), относительно

которой осевой момент инерции минимален.

Теорема. Если сечение имеет ось симметрии, то она, и любая ось, перпендикулярная ей, являются главными осями инерции. Доказательство данного утверждения очевидно из рис.1.6, а.

3

Задача 1.6. Не проводя вычислений, найти положение главных осей, проходящих через точку О плоской фигуры (рис.1.6, б-з).

Указание. Сечение разбить на две фигуры и в первой провести ось симметрии, которая перпендикулярна оси симметрии второй фигуры. Тогда

Juv Ju(1v) Ju(2v) = 0.

Задача 1.7. Для заданных сечений (рис.1.7, а-г) определить разность моментов инерции относительно главных осей, проходящих через точку О.

Указание. Положение главных осей, проходящих через точку О - смотри решение задачи 1.6.

1.2.3. Если сечение имеет более двух осей симметрии (рис. 1.8, а), то все центральные оси являются главными и моменты инерции относительно их будут равны. Доказательство теоремы легко получить из формулы (1.2), если принять, например, что оси y, y1 - неперпендикулярные оси симметрии, т.е. главные центральные оси сечения, и потому Jxy Jx1 y1 = 0 ( у ┴ х, у1 ┴ х1 ). При этом из

выражения для Jx1 y1 имеем Jx = Jу. Учитывая последнее равенство в выражениях

(1.2), убеждаемся, что при любом α центробежный момент инерции равен 0, а осевой момент инерции - постоянен.

Задача 1.8. Определить осевые и центробежный моменты инерция плоской фигуры относительно осей

у1, х1 (рис. 1.8, б-г).

1.2.4. Если главные моменты инерции относительно двух осей, проходящих через некоторую точку сечения, равны, то все оси, проведенные через эту точку, являются главными и моменты инерции относительно их равны. Доказательство теоремы читатель легко получит из выражений (1.2), полагая, что оси х, у

- главные и Jx = Jу.

Задача 1.9: Найти момент инерции сечения (рис.1.9) относительно оси x1.

Задача 1.10. Для плоских сечений (рис.1.10) найти точки, обладающие таким свойством, что все проходящие через них оси являются главными. Оси х, у принять центральными. (для рис.I.10, г считать известными

4

величины Jx, Jу, Jxy). Дополнительно исследовать последний случай (рис.1.10, г), когда Jxy = 0.

Указание. Через искомую точку 0 провести главные оси u, v, параллельные исходным осям х, у. По формулам (I.I) записать выражения для Jи, Jv, Juv. Координаты искомых точек (а; с) определяются из двух условий: Juv = 0 и Ju = Jv.

1.2.5. Если относительно произвольных ортогональных осей моменты инерции равны, то главные оси проходят через начало координат под углом 45° к исходным осям. Доказательство очевидно из формулы (1.3, а).

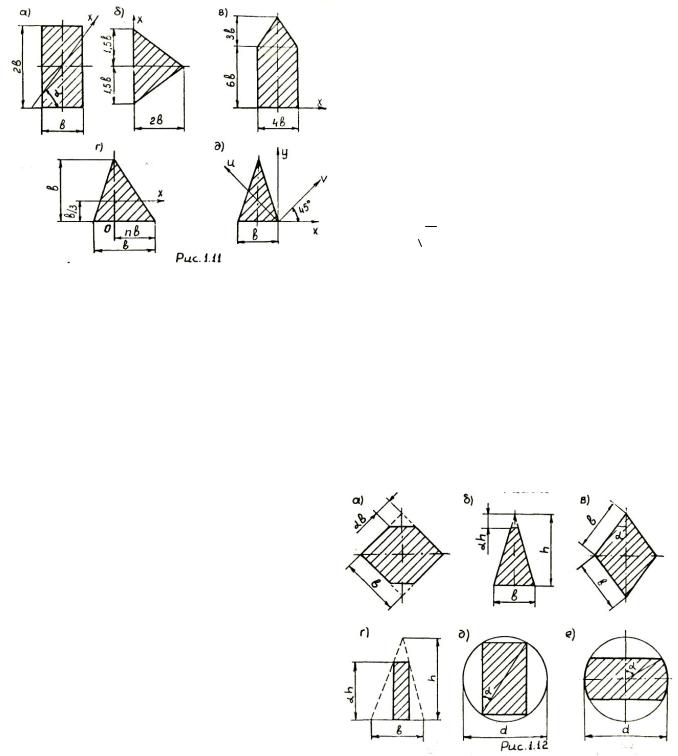
Задача 1.11. а) Для сечений, указанных на рис.1.11, а-в определить на оси x положение точек, через которые главные оси проходят под углом 45° к исходной оси x.

б) Для прямоугольника (рис.1.11, а) найти точки, через которые главные оси проходят под углом 45° к его сторонам, если разность моментов инерции относительно главных осей равна 25b4 .

в) Определить, при каком n максимальный момент инерции относительно оси, проходящей через точку 0 (рис.1.11. г), вычисляется по формуле Jv = Jx +│Jxy│.

г) В равнобедренном треугольнике (рис.1.11, д) определить высоту и разность моментов инерции относительно главных осей u, v, расположенных под углом 45°к осям х, у.

Указание. При решении задач воспользоваться формулами (1.3, а), и (1.3, б).

1.3. Определение экстремальных значений осевых моментов инерции и моментов сопротивления

Если какой-либо параметр сечения является переменным, то записывается выражение для Jx ( Wx ), в которое входит этот параметр, и затем полученное выражение исследуется на экстремум.

Задача 1.12. а) Для заданных сечений (рис.1.12, а-е) определить значение α, при котором осевой момент сопротивления максимален,

б) Для схем на рис.1.12, в-д найти, при каком α осевой момент инерции относительно центральной оси имеет наибольшую величину.

5

2. Построение эпюр внутренних усилий

Данный раздел достаточно подробно рассматривается в традиционном курсе на всех специальностях. По той причине остановимся лишь на некоторых особенностях построения эпюр, которым не уделяется должного внимания на занятиях из-за лимита времени.

Отметим, например, что на практике нередко применяют защемленные подвижные опоры, в которых осуществляется линейное перемещение в горизонтальном или вертикальном направлениях - опоры В и С на рис.2.2, а, а также в обоих направлениях одновременно - опора Л на рис.2.2, б; реакции, возникающие в этих опорах, наказаны на рис.2.2.

Наличие промежуточных шарниров в конструкциях дает возможность составить дополнительные уравнения равновесия для стержней, расположенных с люфой стороны от шарниров.

Дифференциальные зависимости при изгибе:

- позволяют но только контролировать правильность построения эпюр поперечных сил и изгибающих моментов, но и непосредственно получить выражения для Q и М по участках, где интенсивность распределенной нагрузки меняется по сложному закону.

При нагружеиии бруса распределенной моментной нагрузкой интенсивностью ти, дифференциальные зависимости при изгибе (2.2) и (2.3) изменяются - вывод сделать самостоятельно из рассмотрения равновесия элемента dz (рис.2.4, а):

а выражение (2.1) остаётся прежним.

Дифференциальные зависимости справедливы при отсчете координаты z слева направо; положительные направления для внутренних силовых факторов (ВСФ) и иитенсивностей q и ти при изгибе указаны на рис.2.4, а.

Если нагрузка прикладывается перпендикулярно плоскости, в которой расположена ось бруса, то обращаются в нуль все ВСФ, действующие в этой плоскости.

На оси симметрии бруса или конструкции обращаются в нуль симметричные ВСФ - нормальная сила и изгибающие моменты (Nz, Мх, My), если внешняя нагрузка кососимметрична, и кососимметричные ВСФ – поперечиные силы и крутящий момент (Qx, Qy, Mк), - если внешняя нагрузка симметрична.

Задача 2.1. Построить эпюры поперечных сил и изгибающих моментов для балки (рис.2.1), загруженной распределенной нагрузкой, интенсивность которой изменяется го закону параболы.

Указание. Задавшись законом изменения нагрузки в виде = az2 + b·z + с, найти коэффициенты a, b, с из трех условий: при z = 0 и z = 2·l qz = 0; при z = l qz = q0. Далее, используя выражения (2.1) и (2.2),

6

записать:

где постоянные интегрирования C1 (реакция левой опоры) и С2 (Момент на левой oпoрe) определить из граничных условий: при z = 0 и z = l Мх = 0.

Отметим, что в денном примере нам не пришлось предварительно вычислять реакцию левой опоры C1.

Задача 2.2. При заданных условиях нагружения (рис.2.2, а, б) построить эпюры внутренних усилий.

Указание. Реакции в защемленных подвижных опорах для обеих схем, показанные на рис.2.2, а, б, определить или

из условий равновесия всей конструкции (реакции в опоре D на рис.2.2, б, а также RВ и Rc), или из условий равновесия брусьев ОВ, ОС, ОА, ОD расположенных по одну сторону от шарниров О (реактивные моменты МВ, МС, МА; реакция опоры D

на рис.2.2, а).

При составлении выражений для Qy и Мx на участке, где действует синусоидальная распределенная нагрузка, воспользоваться указаниями к предыдущей задаче. Постоянные интегрирования С1 и С2 найти из условий, что в начале участка (при z = 0) имеем: Qу = RD, а Мxо= - МD + RD·l = 0.

Задача 2.3. Для заданных схем (рис.2.3, а-в) вычислить реакции опор, а для кривого бруса (рис.2.3, 6) и рамы (рис.2.3, в) построить также эпюры внутренних усилий.

Указание. Реакцию опоры В (рис.2.3, а) найти из условия, что равнодействующая этой реакции и силы F проходит через точку перегиба О (здесь Мx = 0). Реакция опоры С (рис.2.3, б) проходит через шарнир О, что следует из условия равновесия элемента ОС (ΣМО = 0). Реакция в другой опоре параллельна реакции RС и направлена противоположно ей, т.к. брус загружен парой сил. Для определения реакций опор в раме (рис.2.3, в) учесть, что она загружена кососимметрично и, следовательно, в сечении по оси симметрии (под углом 45°) действует лишь поперечная сила; из равновесия горизонтального (вертикального) участка ОА (ОР) определяется величина этой силы и параллельной ей реакции опоры.

Задача 2.4. Для схем, представленных на рис.2.4, б, в, построить эпюры внутренних усилий.

Указание. Так как распределенная нагрузки q и 2·q (рис.2.4, в) не действует по оси бруса, то она дополнительно создает распределенную по длине моментную нагрузку, интенсивность которой не одинакова на участках бруса.

7

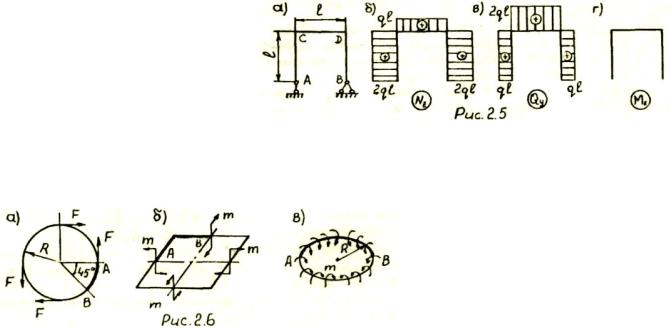
Задача 2.5. По заданным эпюрам ВСФ (рис.2.5, б-г) восстановить внешнюю нагрузку на раму (рис.2.5, а).

Указание. Записав условия равновесия для малых элементов, вырезанных вблизи опорных сечений А, В и узлов рамы С, D, установить сосредоточенные внешние силы (активные и

реактивные), приложенные в указанных сечениях. Затем, используя выражение (2.2, а), найти интенсивности распределенной моментной нагрузки на участках АС,

CD, BD.

Задачи 2.6. He раскрывая статической неопределимости замкнуто контура (pиc.2.6, a-в), определить внутренние усилия и построить их эпюры.

Указание. Учесть кососимметричное и симметричное нагружение и рассмотреть условия равновесия элемента бруса АВ, выделенного на рис.2.6, а-в толстой линией.

8

3. Напряжённо-деформированное состояние. Теории прочности

3.1. Объемное напряженное состояние ( ОНС )

Относительные деформации в направлении главных напряжений определяются по закону Гука

где Е - модуль упругости первого рода (модуль продольной упругости),

μ- коэффициент Пуассона.

Вслучае всестороннего растяжения или сжатия частицы (и любого тела) давлением q [ МПа ] напряжения в каждой точке тела по всем направлениям одинаковы, т.е.

оно действует на площадке, параллельной напряжению σ2 и наклонённой под углом 45° к напряжениям σ1 и σ3.

Для определения главных напряжений при ОНС используют кубическое уравнение вида:

3 J1 2 J2 J3 0 ,

9

В главных осях напряжений инварианты

J1 1 2 3 , J 2 1 2 2 3 3 1 , J 3 1 2 3 .

Задача 3.1. а) Определить, как изменится объем кубика 1х1х1 см (рис.3.1, б-д), треугольной призмы ахhхl = 1х2x20 см (рис.3.1, е), а для схем на рис.3.1, в-е также и площадь верхней грани при заданных условиях нагружения. Вычислить удельную энергию изменения объема и формы. Известно: F = 10 кН; q - 100 МПа;

удельные потенциальные энергии изменения объема и формы достигают наибольшего и наименьшего значений.

Указание. а) Для схем на рис.3.1, б-д главное напряжение в верхней грани кубика определяется как при простом сжатии; напряжения в других гранях находятся из условий

цилиндров (рис.3.2, а-г) найти величину давления q и изменение

объема, если F = 10 кН; А = 0,001 м2;

Е = 2·105 МПа; μ = 0,3; l = I м;

дополнительные условия для каждой

схемы приведены на рисунке. [σ] = 220 МПа.

Указание. Для схемы рис.3.2, а вначале найти εz = - εx/μ; для схемы на рис.3.2, б учесть, что εz = 0 и x y q; для схемы на рис.3.2, в учесть, что

x y q и Ax y x y 0; для схемы на рис.3.2, г имеем z /l .

Задача 3.3. Определить главные напряжения в сечениях стального и медного брусков, вставленных без зазора в жёсткую открытую коробку и нагруженных наружным давлением (рис.3.3). Известно: ЕСТ =2 ЕМ, μСТ, μМ.

Указание. Главные напряжения в верхних гранях обоих брусков равны (-q). Одинаковы также и главные напряжения в обоих брусках в направление оси x - величина их не известна. Эту величину и главные напряжения в брусках вдоль оси у найдем, решив три уравнения совместности деформаций:

ly(CT) y (CT ) a 0; ly(M ) y(M ) a 0; lx(CT) lx(M ) 0,

10