
Расчет на прочность стержневых систем
.pdfМИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РФ
ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ «САМАРСКИЙ ГОСУДАРСТВЕННЫЙ АЭРОКОСМИЧЕСКИЙ УНИВЕРСИТЕТ имени академика С.П. КОРОЛЁВА (НАЦИОНАЛЬНЫЙ ИССЛЕДОВАТЕЛЬСКИЙ УНИВЕРСИТЕТ)»
РАСЧЁТ НА ПРОЧНОСТЬ СТЕРЖНЕВЫХ СИСТЕМ
ПРИ ПОСТОЯННЫХ И ЦИКЛИЧЕСКИ ИЗМЕНЯЮЩИХСЯ НАПРЯЖЕНИЯХ
Рекомендовано редакционно-издательским советом СГАУ
вкачестве заданий и методических указаний
красчётно-проектировочным и курсовым работам
С А М А Р А Издательство СГАУ
2014

УДК СГАУ: 539.3(075)
ББК 30.121
Составители: С.И. Иванов, В.Ф. Павлов, А.П. Филатов,
В.К. Шадрин, В.П. Сазанов, В.А. Кирпичёв
Рецензент канд. техн. наук, доц. В. А. М е х е д а
Расчёт на прочность стержневых систем при постоянных и циклически изменяющихся напряжениях: задания и метод.
указания к расчётно-проектировочным и курсовым работам /
сост.: С.И. Иванов, В.Ф. Павлов, А.П. Филатов [и др]. – Самара:
Изд-во Самар. гос. аэрокосм. ун-та, 2014. – 72 с.
Приведены расчётные схемы и исходные данные к курсовым и расчётно-проектировочным работам по сопротивлению материалов, охватывающие основные разделы второй части курса.
Изложены методика выполнения работ, основные требования к оформлению, даны контрольные вопросы, рассмотрены примеры выполнения работ.
Методические указания предназначены для студентов всех специальностей очной, очно-заочной и заочной форм обучения, изучающих дисциплины «Сопротивление материалов», «Прикладная механика», «Механика материалов», «Механика материалов и конструкций», «Общая теория механики материалов и конструкций».
©Самарский государственный аэрокосмический университет, 2014
2
СОДЕРЖАНИЕ
1 РАСЧЁТ ПЛОСКОЙ СТАТИЧЕСКИ ОПРЕДЕЛИМОЙ РАМЫ….. 4
1.1Задание…………………………………………………………….. 4
1.2Порядок выполнения работы…………………………………….. 4
1.3 |
Пример выполнения работы……………………………………… |
8 |
1.4 |
Контрольные вопросы……………………………………………. 11 |
|
2 РАСЧЁТ ПЛОСКОЙ СТАТИЧЕСКИ НЕОПРЕДЕЛИМОЙ РА- |
13 |
|
МЫ.. |
|
|
2.1Задание…………………………………………………………….. 13
2.2Порядок выполнения работы…………………………………….. 13
2.3Пример выполнения работы……………………………………… 14
2.4Контрольные вопросы……………………………………………. 24 3 РАСЧЁТ ПРОСТРАНСТВЕННОГО БРУСА……………………….. 25
3.1Задание…………………………………………………………….. 25
3.2Порядок выполнения работы…………………………………….. 25
3.3Пример выполнения работы……………………………………… 30
3.4Контрольные вопросы……………………………………………. 37 4 РАСЧЁТ ВАЛА ЗУБЧАТОЙ ПЕРЕДАЧИ…………………………... 39
4.1Задание…………………………………………………………….. 39
4.2Порядок выполнения работы…………………………………….. 39
4.3Пример выполнения работы……………………………………… 42
4.4Контрольные вопросы……………………………………………. 49 5 РАСЧЁТ БАЛКИ ПРИ КОЛЕБАНИЯХ……………………………… 51
5.1Задание…………………………………………………………….. 51
5.2Порядок выполнения работы…………………………………….. 51
5.3Пример выполнения работы……………………………………… 56
5.4Контрольные вопросы…………………………………………….. 68 СПИСОК ЛИТЕРАТУРЫ………………………………………………. 69 Приложения……………………………………………………………… 70
3
1 РАСЧЁТ ПЛОСКОЙ СТАТИЧЕСКИ ОПРЕДЕЛИМОЙ РАМЫ
1.1 Задание
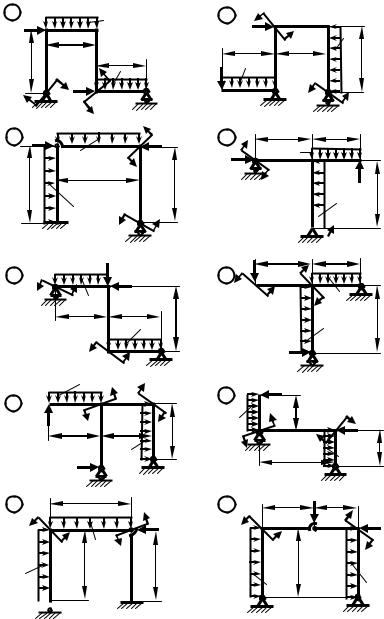
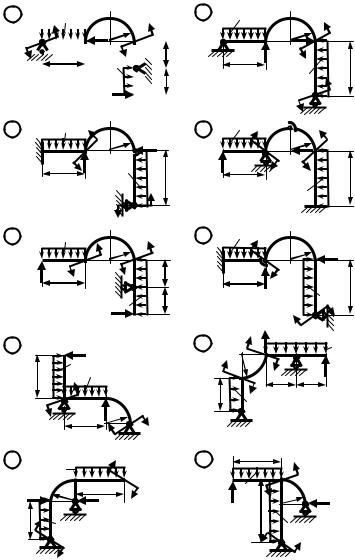
Заданы схема плоской статически определимой рамы (рис. 1, 2), размеры и действующие нагрузки (табл. 1).
Требуется:
построить эпюры нормальных сил, поперечных сил и изгибающих моментов;
подобрать размеры поперечного сечения; определить линейное и угловое перемещения заданного сечения
рамы.
В пояснительной записке следует представить схему рамы, выполненную в масштабе, эпюры поперечных сил, нормальных сил и изгибающих моментов, эпюры от единичных нагрузок и все необходимые расчёты.
1.2Порядок выполнения работы
1.По данным табл. 1 изображают в масштабе схему рамы (рис. 1 или 2), соответствующей заданному шифру.
2.Определяют реакции опор рамы.
3.Строят эпюры нормальных сил N, поперечных сил Q и изгибающих моментов М на каждом участке рамы. Для криволинейных участков предварительно записывают аналитические выражения для N, Q и
М.
4.Подбирают размеры поперечного сечения рамы из условия прочности при изгибе по нормальным напряжениям. В расчётах учитывают,
что материал рамы – Ст. 3 с допускаемым напряжением [ ] = 160 МПа.
5.Проверяют прочность подобранного сечения с учётом действия нормальной силы.
6.Определяют линейные и угловое перемещения в заданном сечении рамы с помощью интеграла Мора. На прямолинейных участках интегралы вычисляют способом Верещагина.
4
1 |
F1 |
|
|
q2 |
|
|
|
|
|
А |
l2 |
A |
|
|
|
|
|
|
|
|
|
||
|
1 |
|
|
|
l |
|
|
|
l |
|
|
|
3 |
|
|
|
|
m1 |
F2 |
|
q1 |
|
|
|
|
|
|
|
|
||
|
|
|
m2 |
B |
|
|
|
3 |
|
F2 |
|
|
|
F1 |
|
|
|
|
q2 |
|
m2 |
B |
|
|
|
|
|
|
|
||
|
3 |
|
|
l1 |
|
|
|
|
|
|
|
|
|
|
|
l |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
l |
|
|
|
q1 |
|
m1 |
A |
|
|
|
|
|
|
|
|
|
5 |
|
m1 |
|
|
F1 |
|
|
|
|
|
|
|
|
||
|
|
B |
q2 |
F2 |
|
|
|
|
|
l1 |
|
|
l3 |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
q1 |
2 |
|
|
|
|
|
|
l |
|
|
|
|
m2 |
|
|
|
|
|
|
|
|
A |
|
|
|
|
|
|
q1 |
|
m1 |
|
|
7 |
|
A |
|
|
|
||
|
|
|
|
|
|
||
|
|
F2 m2 |
|
|
|
|
|
|
|
|
l2 |
|
l3 |
|
1 |
|
|
|
|
|
|
|
l |
|
|
|
F1 |
|
q2 |
|
|
|
|
|
|
B |
|
|
|
|
|
|
|
|
|
|
|
9 |
|
|
l1 |
|
|
|
|
|
B |
|
|
|
|
|
|
m2 |
|
|
|
|
F1 |
||
|
|
|
|
|
|||
|
|
|
|
|
|
||
|
|
|
|
q2 m1 |
|
|
|
q1 |
3 |
2 |
|
l |
l |
F2  A
A
2 |
|
|
|
|
l2 |
F2 |
m1 |
B |
q1 |
q2 |
l3 |
|
||
F1 |
|
|
1 |
|
|
|
|
l |
|
A |
|
|
m2 |
|
4 |
|
l1 |
|
l3 |
|
q1 |
|
||
|
|
A |
||
F1 |
|
m2 |
B |
F2 |
|
|
|
||
|
|
|
|
|
2 l q2
m1
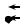
|
|
l3 |
l2 |
6 |
|
F2 |
m2 |
|
A |
m1 |
q1 |
|
|
|
q2 |
1 |
|
l |
F1 |
B |
8 |
A |
|
|
|
F1 |
|
|
|
|
|
|
|
|
|
q2 |
3 |
B |
|
m2 |
l |
|
|||
m1 |
|
|
F2 |
2 |
|
|
|
||
|
|
|
|
|
|
|
|
|
l |
|
l1 |
|
q1 |
|
10 |
l2 |
|
l3 |
BF2 |
|
|
|
||
m2 |
A |
F1 |
|
|
|
|
|
|
|
|
|
|
|
m1 |
|
1 |
|
|
|
|
l |
|
|
|
|
q1 |
|
|
q2 |
Рис. 1. Статически определимые рамы с прямолинейными участками
5
1
m2
|
|
|
|
q1 |
|
R |
m1 |
|
||
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
l1 |
A |
F2 |
|
|
/2 |
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
l |
||||
|
|
|
|
|
|
|
q2 |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
/2 |
|
|
|
|
|
|
|
|
F1 |
|
|
|
|
|
|
|
|
|
|
B |
|||
|
|
|
|
|
|
|
2 |
|||
|
|
|
|
|
|
|
|
|
|
l |
|
|
|
|
|
|
|
|
|
|
|
2 |
q2 |
|
|
||
|
l2 |
A F1 |
R m1
F2 B
q1 |
l |
|
1 |
m2
3 |
q2 |
m1 |
R |
F2 |
|
|
A |
||
|
l1 |
F1 |
q1 |
2 |
|
|
|
|
l |
B m2 |
4
A
F1
q2 |
|
R |
m2 |
|
|
B |
|
|
|
|
|
l1 |
|
F2 |
|
m1 |
|
|
|
|
|
2 |
|
|
|
q1 |
l |
5 |
|
q2 |
R |
|
|
B |
|
|
|
||
|
|
m2 |
/2 |
||
F |
l1 |
m1 |
|||
|
2 |
||||
1 |
|
l |
|||
|
|
|
q1 |
/2 |
|
|
|
|
l |
||
|
|
|
|
2 |
|
|
|
|
F2 |
A |
7 |
|
A F1 |
|
|
|
1 |
q2 |
|
|
|
q1 |
|
|
|
|
l |
|
|
|
|
|
|
B |
|
|
m2 |
F2 |
R |
m1 |
|
|
|||
|
|
l2 |
|
|
9 |
|
q2 |
|
|
|
|
|
B |
|
|
|
|
|
|
F2 |
A |
R |
l1 |
m1 |
|
|
|
F1 |
|
2 |
|
|
|
|
l |
|
q1 |
|
|
|
|
m2 |
|
|
6 |
q1 |
m2 |
|
|
|
|
|
|
R |
F1 |
|
|
l2 |
|
|
A |
|
|
|
F |
|
|
|
|
|
|
|
1 |
|
|
|
|
2 |
q2 |
l |
|
|
|
|
|
|
|
|
|
m1 |
|
|
|
|
B F2 |
B |
|
|
8 |
m1 |
|
q2 |
||
|
m2 |
R |
l2/2 l2/2 F1 |
||
|
A |
||||
|
1 |
q1 |
|
|
|
l |
|
|
|
||
10 |
l2 |
B m1 |
|
|
|
||
A |
|
|
|
q1 |
R |
F2 |
|
F1 |
|
||
|
1 |
q2 |
|
|
l |
|
|
|
|
m2 |
|
Рис. 2. Статически определимые рамы с криволинейными участками
6
Т а б л и ц а 1. Параметры для статически определимых рам
строки№ |
схемы№ |
m |
m |
F |
|
F |
q |
q |
l |
l |
l |
мR, |
Сечение |
|
|
|
|
|
|
|
|
|
|
|
кН·м |
кН·м |
, кН |
|
, кН |
кНм/ |
кНм/ |
, м |
, м |
, м |
|
|
|
|
|
Форма поперечного сечения |
|||||
|
|
1 |
2 |
1 |
|
2 |
1 |
2 |
1 |
2 |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
, |
, |
|
|
|
, |
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
1 |
4 |
20 |
0 |
40 |
|
0 |
15 |
0 |
3 |
2 |
4 |
1 |
А |
|
I – двутавр |
|||||||
2 |
1 |
0 |
40 |
0 |
|
30 |
0 |
20 |
4 |
3 |
2 |
1,5 |
В |
|
┘└ – два неравнобоких угол- |
|||||||
|
|
ка |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
3 |
7 |
-50 |
0 |
30 |
|
0 |
10 |
0 |
2 |
4 |
4 |
2 |
А |
|
I I – два двутавра |
|||||||
4 |
2 |
0 |
-40 |
0 |
|
20 |
0 |
-15 |
3 |
2 |
2 |
2,5 |
В |
|
○ – круг |
|||||||
5 |
3 |
30 |
0 |
-20 |
|
0 |
-10 |
0 |
4 |
4 |
2 |
1 |
А |
|
[ ] – два швеллера |
|||||||
6 |
10 |
0 |
-30 |
0 |
|
-30 |
0 |
10 |
2 |
3 |
4 |
1,5 |
В |
|
□ – квадрат |
|||||||
7 |
4 |
40 |
0 |
-30 |
|
0 |
20 |
0 |
2 |
2 |
4 |
2 |
А |
|
|
|
|
|
|
|
|
– два швеллера |
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||
8 |
5 |
0 |
-20 |
0 |
|
40 |
0 |
-20 |
3 |
3 |
2 |
2,5 |
В |
|
] [ – два швеллера |
|||||||
9 |
9 |
-30 |
0 |
-40 |
|
0 |
-15 |
0 |
5 |
4 |
3 |
1 |
А |
|
|
|
|
|
|
– четыре равнополочных |
||
|
|
|
|
|
|
|||||||||||||||||
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
уголка |
|||||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
6 |
0 |
30 |
0 |
|
-20 |
0 |
15 |
3 |
5 |
4 |
2 |
В |
|
I – двутавр |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
а |
|
|
|
б |
|
|
|
в |
|
г |
д |
|
|
|
|
|
|
|
|
е |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
7
7
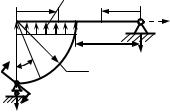
1.3 Пример выполнения работы
Для рамы, изображённой на рис. 3, построить эпюры нормальных сил, поперечных сил и изгибающих моментов, подобрать размеры поперечного сечения и определить линейные и угловое перемещения сечения А при следующих данных: q = 20 кН/м, m = 40 кН·м, l = R = 2 м, поперечное сечение – ][ – два швеллера.
Определим реакции опор:
|
z 1 |
20 кН/м |
|
||
|
|
|
C |
||
A |
|
|
|
|
|
|
|
D 2 |
|
H |
|
|
|
|
м |
||
|
φ |
|
|
|
20 кН |
|
|
2 м |
|
|
|
|
|
|
|
|
|
B |
|
40 кН·м |
|
|
|
|
|
|
|
||
20 кН Рисунок 3 – Расчётная схема
рамы
M C V B 4 40 20 2 3 0 , |
V B 20 кН ; |
x H C 0; |
|
M B VC 4 40 20 2 1 0, |
VC 20 кН. |
Проводим проверку:
y 20 20 2 20 0.
Строим эпюру нормальных сил (рис. 4, а). На участке BD
N ( ) V B sin 20 sin , |
|
|
при 0 N 0 , при |
|
N 20 кН. |
2 |
||
На других участках нормальные силы отсутствуют. |
||
Строим эпюру поперечных сил Q (рис. 4, б). |
||
На участке BD |
|
|
Q ( ) V B cos 20 cos , |
|
|
при 0 Q 20кН. , при |
|
Q 0. |
2 |
||
На участке CD Q VC 20 кН const . |
||
На участке AD Q q z1 |
20 z1 , при z = 0 Q = 0, при z = 2 м |
|
Q = 40 KH.
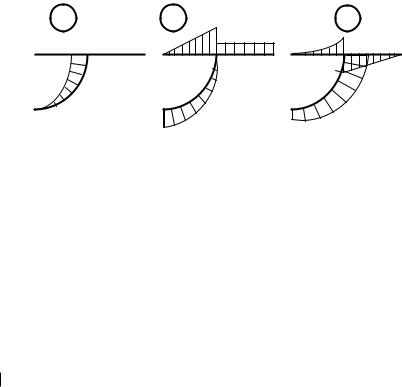
Строим эпюру изгибающих моментов (рис. 4, в).
8
На участке BD
M ( ) m V B R sin 40 20 2 sin 40 40sin , |
|
||||||||
при 0 M 40кНм , при |
|
M 80 кН м . |
|
||||||
2 |
|
||||||||
На участке AD M |
q z 12 |
|
20 z 12 |
12 |
при z1 = 0 |
M = 0, при z1 = 2 м |
|||
|
|
|
|
|
10 z |
||||
2 |
|
|
2 |
||||||
|
|
|
|
|
|
|
|
||
M = 40 кH·м. |
|
|
|
|
|
|
|
|
|
На участке СD M 10 z 2 |
при z2 |
|
= 0 М = |
0, при z2 = 2 м |
|||||
М = – 40 кH·м. |
|
|
|
|
|
|
|
|
|
N |
, кН |
Q |
, кН 40 |
|
|
M |
, кН·м |
2 0 |
|
|
20 |
|
40 |
|
80 |
|
|
|
|
|
|
||
а ) |
|
б ) |
|
в ) |
40 |
|
|
20 |
40 |
Рисунок 4 – Эпюры внутренних сил
Подберём поперечное сечение, составленное из двух швеллеров, из условия прочности только при изгибе:
W ][x |
|
J ][x |
|
|
|
2 |
J [x |
2 W [x ; |
|
|
||||||
|
y |
|
|
|
|
|
y |
|
|
|
||||||
|
|
|
|
наиб |
|
|
наиб |
|
|
|
||||||
[ |
|
|
|
M |
|
наиб |
|
|
80 10 3 |
250 см |
3 |
|
||||
|
|
|
|
|
||||||||||||
W x |
|
|
|
|
|
|
. |
|||||||||
|
|
2 |
|
2 160 10 6 |
|
|||||||||||
Полученному значению удовлетворяет швеллер № 24 а с характеристиками: W [x = 265 см 3, J [x = 3180 см 4, A [ = 32,9 см 2.
Проверим подобранное сечение по полному условию прочности:
|
|
наиб |
M |
наиб |
|
|
N |
|
|
80 10 3 |
|
20 10 3 |
154,0 МПа , |
|
|||||||||||||
|
|
|
|
|
|
2 265 10 6 |
2 32,9 10 4 |
||||||
|
|
|
2 W [x |
2 A[ |
|
|
|
||||||
условие прочности выполняется.
Определим вертикальное перемещение сечения А. Для этого приложим в направлении искомого перемещения единичную силу, определим
9
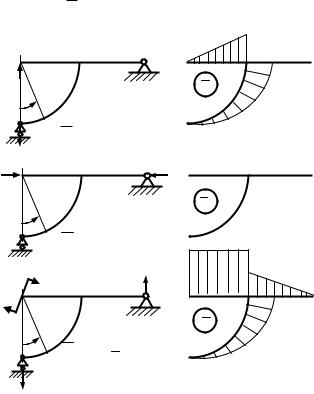
реакции опор от единичного нагружения и построим эпюру изгибающих моментов M 1 (рис. 5, а).
|
|
|
2 |
A |
D |
С |
2 |
1 |
|
M 1 |
, м |
|
|
||
а ) φ |
|
|
|
В |
M 1 ( ) 1 2 |
sin |
|
1 |
|
||
|
|
|
|
A |
|
D |
С |
|
1 |
|
|
|
|
|
б ) |
|
|
|
|
M 2 |
φ |
|
|
|
|
|
|
|
|
|
|
|
В |
|
|
M 2 ( ) 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
1/2 |
A |
|
1 |
D |
1 / 4 |
|
|
|
С |
|
||
|
|
|
1/2 |
||
|
|
|
|
|
|
в ) |
|
|
|
|
M 3 |
φ |
|
M 3 ( ) 1 |
|
|
|
В |
|
|
2 sin |
|
|
|
|
4 |
|
|
|
|
|
|
|
|
1/4
Рисунок 5 – Эпюры моментов от единичных нагружений
На участке BD интеграл Мора вычислим непосредственно; на участке AD – способом Верещагина; на участке CD интеграл равен нулю:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
1 |
|
3 |
|
|
E J x 1 |
M M 1 d z |
M M 1 d z ( 40 |
40sin ) 2sin 2 d |
40 2 |
2 |
|||||||||||||
3 |
4 |
|||||||||||||||||
|
BD |
|
|
|
AD |
|
|
|
0 |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
40 1 40 |
|
|
|
325,7 кН м |
3 |
; |
|
|
|
|
||||||
4 |
4 |
40 |
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
1 y A |
|
|
325,7 10 3 |
|
|
|
25,60 мм. |
|
|
|
|
|
||||||
2 10 11 2 3180 10 8 |
|
|
|
|
|
|||||||||||||
Знак «плюс» указывает на то, что направление искомого перемещения совпадает с направлением единичной силы, т.е. сечение А движется вверх.
10
