
Электротехника+лекции
.pdf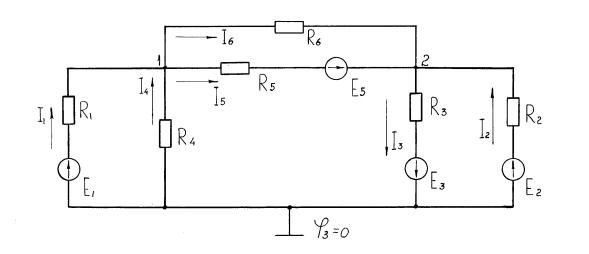
заземлить, т.е. принять потенциал его равным нулю. При этом число неизвестных уменьшается с у до (у – 1).
Число неизвестных в методе узловых потенциалов равно числу уравнений,
которые нужно составить для схемы по первому закону Кирхгофа. В тех случаях, когда (у – 1) меньше числа независимых контуров в схеме, данный метод является более экономным, чем метод контурных токов.
Обратимся к схеме рис. 1.28.
Рис. 1.28. Схема четырехконтурной электрической цепи с четырьмя источниками э.д.с.
Принимаем потенциал одного из узлов схемы, например, третьего,
равным нулю, обозначим положительные направления токов и записываем уравнения по первому закону Кирхгофа для первого и второго узлов:
I6 + I5 – I1– I4 = 0;
I3 – I2 – I6 – I5 = 0.
Токи в ветвях схемы:
I6 = (φ1–φ2) g6; I5 = (φ1–φ2 + Е5) g5 ;
I2 = (–φ2 + Е2) g2; I3 = (φ2 + Е3) g3 ;
I1 = (–φ1 + Е1) g1; I4 = (–φ1 ) g4 .
Подставим значения токов в уравнения, составленные по первому закону Кирхгофа:
φ1 g6 – φ2 g6 +φ1 g5 – φ2 g5 + Е5g5 + φ1 g1 – Е1g1 + φ1 g4 = 0
φ1 g3 +E3 g3 + φ2 g2 – E2 g2 – φ1g6 + φ2 g6 – φ1g5 + φ2 g5 – E5 g5 = 0.
Производим группировку членов:
φ1 (g6 + g5 + g1 + g4) – φ2 (g6 + g5) = Е1g1 – Е5g5
–φ1 (g6 + g5) + φ2 (g3 + g2 + g6 + g5) = Е2g2 – Е3g3 + Е5g5 ,
где: g6 + g5 + g1 + g4 = g11 – собственная проводимость первого узла; g3 + g2 + g6 + g5 = g22 – собственная проводимость второго узла; g6 + g5 = g12 = g21 – общая узловая проводимость.
Окончательно получаем:
φ1 g11 – φ2 g12 = Eg
1
–φ1 g21 + φ2 g22 = Eg .
2
В результате решения системы уравнений известными методами определяем φ1 и φ2.
Подставляя значения φ1 и φ2 в уравнения для токов, находим действительные токи в ветвях схемы.
1.16.5. Метод эквивалентного генератора (метод холостого хода и
короткого замыкания)
На практике часто бывает необходимо изучить режим работы только одной из ветвей сложной электрической схемы, при этом не следует производить расчет всей схемы, а целесообразно воспользоваться методом эквивалентного генератора. Согласно этому методу в схеме выделяется исследуемая ветвь и расчет производится в следующем порядке:
1)произвольно выбираем направление тока в исследуемой ветви;
2)определяем напряжение холостого хода Uхх на зажимах разомкнутой исследуемой ветви;
3)находим входное (эквивалентное) сопротивление схемы со стороны зажимов разомкнутой ветви Rэ’ если известен ток короткого замыкания
I |
., |
то R |
U xx |
; |
|
||||
|
к.э |
Э |
Ik .э. |
|
|
|
|
|

4) находим ток в исследуемой ветви:
I U xx E , RЭ R
где: R – сопротивление ветви, в которой определяется ток;
Е – э.д.с. в исследуемой ветви, если ветвь не содержит э.д.с, то Е = 0.
Знаки «плюс» или «минус» в последнем выражении выбираются в соответствии с законом Ома для участка цепи, содержащего э.д.с.
Рассмотрим применение метода эквивалентного генератора на примере схемы рис. 1.29, допустим Е2 = Е3 = Е4 = 20 В, Е5 = 50 В, R1 = R2 = R3 = R4 = 2 Ом; R5 = 3 Ом, требуется определить ток в ветви bс.
Рис. 1.29. Схема трехконтурной электрической цепи с четырьмя источниками э. д. с.
Указываем направление тока в ветви bс и определяем напряжение холостого хода Ubcxx на зажимах ветви bс. Схема в этом случае имеет вид,
показанный на рис. 1.30.
Для нахождения Ubcxx вначале находим ток I1 и напряжение Uac по методу двух узлов:
I1 |
|
|
E2 |
|
|
20 |
|
5А |
|
|
|
|
|
|
||
|
R1 R2 |
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
2 2 |
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
50 |
1 |
|
20 |
1 |
|
||||
|
|
|
E5 g5 |
E4 g 4 |
|
|
|
|||||||||
|
|
|
3 |
2 |
|
|||||||||||
U ac |
|
|
|
|
|
|
|
|
|
|
|
|
|
8В |
||
g5 |
g 4 |
|
1 |
|
|
1 |
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
3 |
2 |
|
|
|
||
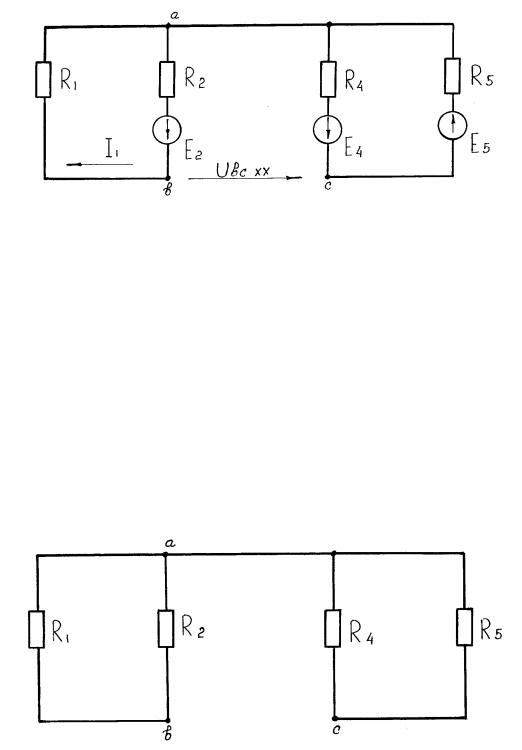
Рис. 1.30. Схема для определения напряжения холостого хода Ubcxx по методу эквивалентного генератора
Напряжение Ubcxx определяется по второму закону Кирхгофа, обходя контур bасb:
Ubcxx = R1I1 + Uac = 2·5+8 = 18 B.
Определяем эквивалентное сопротивление относительно зажимов bc,
схема в этом случае имеет вид, показанный на рис. 1.31:
R |
R1 R2 |
|
R4 R5 |
|
2 2 |
|
2 3 |
|
2,2Ом |
|
R1 R2 |
R4 R5 |
2 2 |
2 3 |
|||||||
Э |
|
|
|
|
||||||
Рис. 1.31. Схема для определения эквивалентного сопротивления относительно зажимов bс no методу эквивалентного генератора
Находим ток в исследуемой ветви bс :
Ibc |
|
Ubcxx E3 |
|
18 20 |
0,476 |
А, |
|
RЭ R3 |
2,2 2 |
||||||
|
|
|
|
|
т.е. ток Ibc в схеме имеет направление, противоположное выбранному.
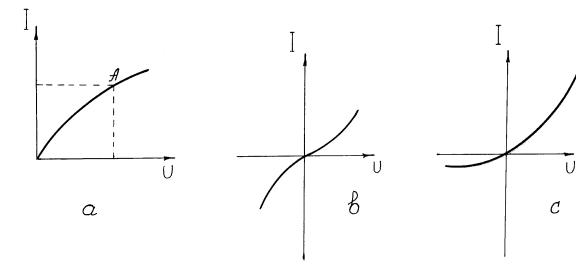
1.17. Нелинейные элементы в цепях постоянного тока |
|
Нелинейные элементы (НЭ) подразделяются на |
управляемые и |
неуправляемые. В управляемых НЭ, в отличие от неуправляемых, кроме основной цепи, есть еще управляющая цепь, воздействуя на ток или напряжение которой, можно деформировать ВАХ основной цепи. Для неуправляемых НЭ ВАХ изображается одной кривой, а для управляемых — семейством кривых. В группу неуправляемых НЭ входят: лампы накаливания,
выпрямительные диоды, стабилизаторы и т. д. В группу управляемых НЭ входят три и более электродные лампы, транзисторы и т. д. На рис. 1.32
показаны ВАХ некоторых НЭ. Чем больше протекающий через нить лампы накаливания ток, тем нить сильнее нагревается и тем больше становится ее сопротивление. Некоторые типы термосопротивлений имеют симметричную ВАХ. Полупроводниковые диоды пропускают ток практически только в одном, проводящем направлении.
Рис. 1.32. Типовые ВАХ: a – лампы накаливания; b – термосопротивления; c – полупроводникового диода
Каждый НЭ характеризуется ВАХ, статическим и дифференциальным сопротивлениями.

Статическое сопротивление Rcm равно отношению напряжения к току в данной точке, например, в точке А рис. 1.32, а:
Rст UI .
Дифференциальное (динамическое) сопротивление Rд равно отношению бесконечно малого приращения напряжения dU к соответствующему приращению тока dI:
Rд dUdI .
Дифференциальное сопротивление характеризует НЭ при достаточно малых отклонениях от предшествующего состояния, используется при исследовании вопроса об устойчивости режимов работы нелинейных цепей.
1.18. Методы расчета цепей постоянного тока с нелинейными
элементами
Существует два метода расчета: аналитический и графоаналитический.
Первый метод ввиду его сложности в данном курсе не рассматривается.
Второй метод заключается в построении общей ВАХ всей цепи по ВАХ отдельных элементов, которые снимаются экспериментально, могут быть заданы в графической или табличной форме, взяты из паспорта НЭ.
Расчет цепи с последовательными соединением НЭ. На рис. 1.33 два нелинейных элемента соединены последовательно. Как известно, ток I при последовательном соединении элементов на всех участках цепь одинаков, а
напряжение U = U1 + U2 согласно второму закону Кирхгофа.
На рис. 1.34. приведены ВАХ первого и второго НЭ, а также ВАХ всей цепи, которая построена следующим образом. Проводим пунктиром прямые параллельно оси напряжения. Чем больше прямых, тем точнее получается расчет. Складывая напряжения точек пересечения, получаем напряжение точки кривой I = f(U). Соединив все точки, получаем ВАХ всей цепи.
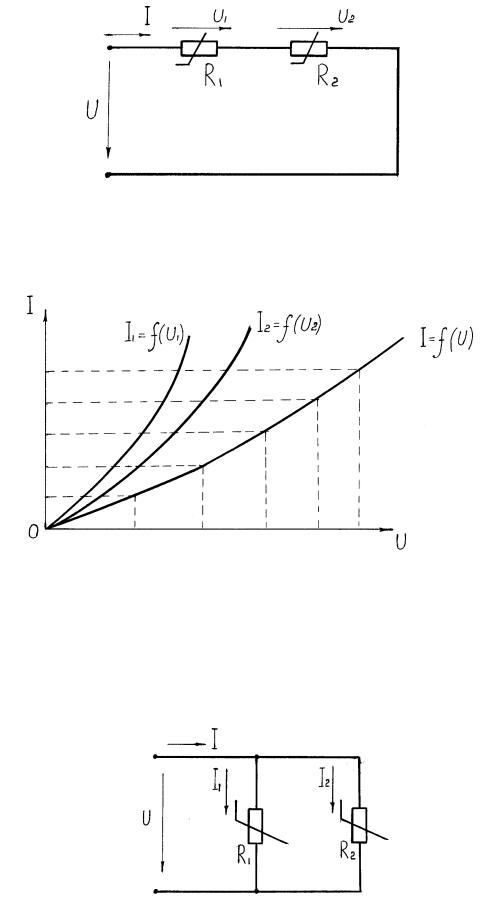
Рис. 1.33. Последовательное соединение двух нелинейных элементов
Рис. 1.34. Построение общей ВАХ всей цепи при последовательном соединении нелинейных элементов
Расчет цепи с параллельным соединением НЭ. По первому закону Кирхгофа для цепи рис. 1.35 можно записать I = I1 + I2. Напряжение на
Рис. 1.35. Параллельное соединение двух НЭ
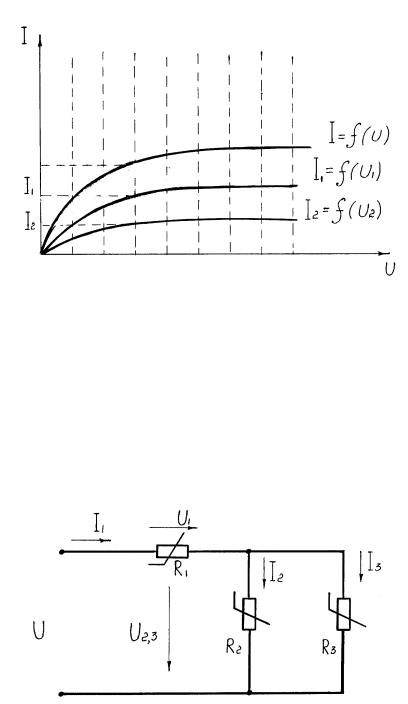
элементах цепи равно входному U. Построение общей характеристики I = f(U)
производится путем складывания ординат кривых I1 = f(U1) и I2 = f(U2) на рис.1.36.
Рис. 1.36. Построение общей ВАХ всей цепи при параллельном соединении НЭ
Расчет цепи со смешанным соединением НЭ. На схеме рис. 1.37. R2 и R3
соединены параллельно, но последовательно с R1, поэтому расчет проводим в два этапа. Вначале строим общую ВАХ I2,3 = f(U2,3) для второго и третьего элемента, затем ВАХ всей цепи I = f (U), как показано на рис. 1.38.
Рис. 1.37. Смешанное соединение трех нелинейных элементов
На рис.1.34. 1.36 и 1.38 показаны построения для одной точки ВАХ I = f(U).

Рис. 1.38. Построение общей ВАХ всей цепи при смешанном соединении НЭ
2. ЭЛЕКТРИЧЕСКИЕ ЦЕПИ ОДНОФАЗНОГО ПЕРЕМЕННОГО ТОКА
2.1. Области применения электрической энергии |
однофазного |
переменного тока |
|
1. Питание электродвигателей бытовых приборов – холодильников, |
|
стиральных машин, пылесосов, ручного электроинструмента. |
|
2. Питание бытовой радиоэлектронной аппаратуры – |
телевизоров, |
видеоплейеров, радиотелефонов и т.д. |
|
3.Электрифицированный железнодорожный транспорт.
4.Освещение (лампы накаливания, люминесцентные лампы, галогеновые лампы).
Для бытовых электроприемников в России принято напряжение 220 В
частотой 50 Гц. В большинстве стран Европы в качестве стандартной частоты принята f = 50 Гц, а Англии – 40 Гц, в США и Японии – 60 Гц. Частота и напряжение питания приемников выбираются исходя из технико-
экономических условий.
Некоторые электротехнические устройства работают при более высокой частоте. В авиации, например, применяется синусоидальный ток с частотой
400 Гц, так как при этой частоте снижаются вес и габариты авиационного электрооборудования.
Для нужд железнодорожного транспорта применяют пониженную частоту
25 Гц (50/2) и 16 23 Гц (50/3).
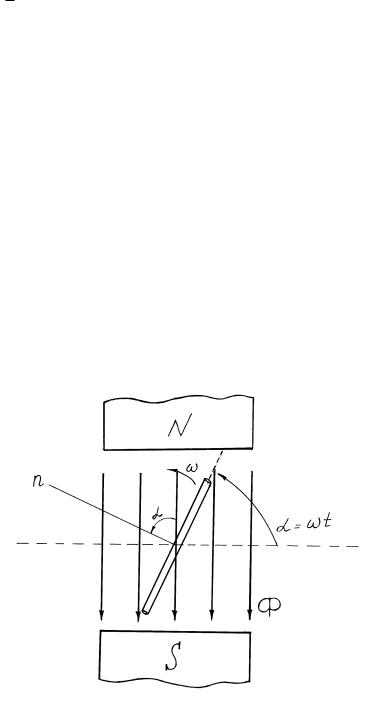
2.2. Получение однофазной синусоидальной э.д.с.
Поместим рамку, состоящую из одного витка, в однородное поле постоянных магнитов (рис. 2.1). Рамка вращается с постоянной угловой скоростью ω=const. В соответствии с законом электромагнитной индукции в ней будет наводиться э.д.с:
e |
dФ |
|
d (Фm cos t) |
Фm sin t Em sin t , |
|
dt |
dt |
||||
|
|
|
где:
Фm – амплитудное (максимальное) значение магнитного потока;
α = ωt – угол между направлением поля и нормалью к плоскости рамки;
Еm = ωФm– амплитудное (максимальное) значение э.д.с.
Рис. 2.1. Рамка в однородном поле
