Savchenko_O_Ya__FMSh_NGU__Zadachi_po_fizike
.pdf
5.10.5.13 % воды.
5.10.6.Смесь 100,5 г воды и 30,5 г льда при 0 ◦C.
5.10.7.m = 98 г/с.
5.10.8 . x ≈ 0,11 м.
5.10.9. а. Пока в кастрюле есть вода, температура дна порядка 100 ◦C. б. Можно.
5.10.11.Между поверхностью раскаленной плиты и каплей образуется прослойка пара, затрудняющая подвод тепла к воде.
5.10.12.Низкая температура воздуха в сосуде Дьюара поддерживается кипением воздуха,
анизкая температура твердой углекислоты — сильным испарением ее с поверхности.
5.10.13.Происходит испарение льда в сухом воздухе.
5.10.14.v ≈ 8 м/с.
5.10.15 . Четыреххлористый углерод выкипает в 25 раз быстрее.
5.10.16.Чтобы предотвратить конденсацию пара.
5.10.17.Нельзя.
5.10.18.При критической температуре жидкость и пар неразличимы.
5.10.19.Быстрее.
5.10.20.m = 11,7 г.
5.10.21.P = 0,2 МПа, A = 35 кДж.
5.10.22.P = 0,37P0.
5.10.23.v = mλRT/[P0(µq + RT )]. A = mλRT/(µq + RT ).
5.10.24 . h ≈ 580 м.
5.10.25.5 % воды.
5.10.26.6 % льда.
5.10.27.а. n = exp(mgh/RT ) = exp(2mσ/ρr). б. h = 15 см.
5.10.28.t = 2ϕλµH2OPн/(7RP ) = 23 ◦C.
5.10.29.Уменьшится в два раза.
5.10.30.P = P0(R/r)2.
5.10.31 . P = 2√P0(R/L)2.
5.10.32.а. В m n раз. б. P = 200P0.
5.10.33.a = 1,0 м/с2.
5.10.34.m1 = 1,7 кг/с, m2 = 170 кг/с.
5.10.35 . T ≈ 1720 К.
§ 5.11. Тепловое излучение
5.11.1.а. Φ ≈ 0,2 кВт. б. ϕ = 89 МВт/м2.
5.11.2.T1 ≈ 600 ◦C, T2 ≈ 2000 ◦C.
5.11.3 . w = 7,56 · 10−16 T 4 Дж/м3.
5.11.5. а. Кварц, в отличие от стали, почти не поглощает видимый свет, поэтому при нагревании он в видимой области излучает значительно слабее.
б. В отличие от черного угля, почти полностью поглощающего видимый свет, белый мел этот свет отражает. Поэтому при нагревании мел излучает значительно меньше света и вы-
глядит на фоне сильно излучающего угля темным. |
|
|
|
|
|||||||||||||||
5.11.6 . а. T = T0/√2. |
б. |
2T = q |
|
|
2 |
|
|
|
|||||||||||
(T1 + T2 )/2. |
|
|
|
||||||||||||||||
|
|
|
|
4 |
|
|
|
|
|
4 |
4 |
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
5.11.8. |
|
. T = |
p |
|
|
|
|
|
|
|
. Φ ≈ 4 · 10 |
|
|
|
. |
|
. T = 140 ◦C. |
||
|
|
|
− |
|
◦ |
|
|
|
|
|
|||||||||
5.11.7. |
а. T = T0 |
ε(R/2L) . |
б. ϕ = 1,7 |
кВт/м . |
|
|
|
||||||||||||
|
а |
|
200, 70, |
|
35 |
C. |
б |
|
|
|
26 Вт |
|
в |
|
|||||
5.11.9.T = 2,4 К.
5.11.10.T = 20 ◦C.
5.11.11 . Φ = |
|
|
|
ε1ε2 |
|
|
|
σS(T14 − T24). |
|
|
|
|
|
||||||
ε1 + |
ε |
ε |
ε |
|
|
|
|
|
|
||||||||||
|
|
2 |
− |
1 |
|
2 |
|
|
|
|
|
|
|
|
|
||||
5.11.12. а. T 0 = T/ |
4 |
|
б. n = 32. |
|
|
|
|
|
|||||||||||
√2. |
|
|
|
|
|
||||||||||||||
5.11.13 . T = |
|
|
|
|
T0 |
|
|
. |
|
|
|
|
|
|
|
|
|||
|
p |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
4 |
|
6,5 + 4R/r |
|
|
|
|
|
|
|
|
|
||||||
5.11.14 . T = s |
|
|
|
|
|
|
|
|
|
|
|||||||||
T14 − T24 + |
T1 |
+ 2 − ε (T14 |
− T24) κ |
|
. |
||||||||||||||
|
|
4 |
|
|
|
|
|
|
|
|
|
|
ε |
|
h |
|
4 |
|
|
21 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
321 |
|
r
|
SΦ |
1 |
1 |
|
SΦ |
|||
5.11.16. а. a = |
|
. б . v = |
|
|
|
|
|
. |
|
2πR2mc |
R1 |
− R2 |
πmc |
||||
5.11.17. а. На хвост кометы действует давление солнечных лучей. б. r ≈ 1 мкм.
Глава 6. ЭЛЕКТРОСТАТИКА
§ 6.1. Закон Кулона. Напряженность электрического поля
6.1.1.а. F = 1,8 · 104 Н. б. F = 2,3 · 10−8 Н. В 4,17 · 1042 раз.
6.1.2.q ≈ 1,05 · 10−5 Кл ≈ 3,16 · 104 СГС.
6.1.3.а. E = 1 В/м = 3,3 · 10−5 СГС. б. E = 3 · 105 В/м = 10 СГС.
6.1.4. |
На расстоянии 1 |
м E |
1 |
= 9 |
· |
1010 В/м = 3 |
· |
106 |
СГС; на расстоянии 20 м |
|||
|
8 |
В/м = 7,5 · 10 |
3 |
СГС. |
|
|
|
|
||||
E2 = 2,25 · |
10 |
|
|
|
|
|
|
|
|
|
||
На заряд 0,001 Кл F1 = 9 · 107 Н, F2 = 2,25 · 105 Н;
на заряд 1000 СГС F1 = 3 · 109 дин, F2 = 7,5 · 106 дин.
6.1.5.F = 2,56 · 109 Н.
6.1.6.q = 3,5 · 103 Кл.
6.1.7. T12 |
= |
q1(4q2 + q3) |
, |
T23 |
= |
q3(4q2 + q1) |
. |
16πε0l2 |
|
||||||
|
|
|
|
|
16πε0l2 |
||
6.1.8. На расстоянии x = l√q1/(√q1 + √q2 ) от заряда q1. Да. Нет.
√
6.1.9. q = l 8πε0mg.
12 q2
6.1.10.T = 4πε0l2 Q − 3√3 .
6.1.11.β = 2 arctg(q/Q)2/3, α = π − β.
6.1.12.r = 1,4 · 10−8 см.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
√ |
|
|
|
|
|
|
|
(8πε |
ml3). |
|
|
|
|||||||||||
6.1.13. ω = qq(3 |
2 − 4)/ |
2 |
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|||||||||||||||
6.1.14 . qмин = 32πε0mgR |
/Q. |
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
q2√ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
a2 + l2 |
|
|
|
|
|
|
|
|
|
||||||||||||||
6.1.15. k = |
32πε0a3(√ |
|
|
|
|
|
− l) |
. |
|
|
|
|
||||||||||||||||||
a2 + l2 |
|
|
|
|||||||||||||||||||||||||||
6.1.16 . T = 8πε0l2 4 |
+ |
|
|
3 |
|
!. |
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
q2 |
|
9 |
|
|
√ |
3 |
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
6.1.17. E1 = 0, E2 = Qh/[(4πε0(R2 + h2)3/2]. |
|
|
|
|||||||||||||||||||||||||||
6.1.18 . E = ρl/[4πε0x(l + x)]. |
|
|
|
|
|
|
|
|
||||||||||||||||||||||
6.1.19. а) E = σ/(6ε0); |
б) E = (σ1 − σ2)/(4ε0); |
в) E = σ/(2ε0); |
||||||||||||||||||||||||||||
q |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
г) E = |
σ2 |
+ σ2 |
+ σ2 |
σ1σ2 |
− |
σ2σ3 |
− |
σ1σ3/(3ε0); д ) E = ρh(1 |
− |
cos α)/(2ε0); |
||||||||||||||||||||
е ) E = |
√ 1 |
2 |
|
|
3 − |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
3 lρ/(12ε0). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
6.1.20.б. Да. √
6.1.21.а. q = 10 Q. б. q = 9Q.
§ 6.2. Поток напряженности электрического поля. Теорема Гаусса
6.2.1.а. Φ = El2/2. б. Φ = −Eh2, Φ = Eh2.
6.2.2.Φ = E cos α · π(R2 − r2).
6.2.4.F = σΦ.
6.2.5.а. F1 = F2 = qσ/(2ε0), E = σ/(2ε0). б. F = σq/(4ε0).
♦ |
|
а |
|
при |
Q/(4ε r2) при r > R; |
б) E = ρ/(2πε |
r); |
в) E = σ/(2ε |
); |
||
6.2.6. |
|
) E = 0 |
|
r < R, E = 3 |
0 2 |
) при r > R; |
0 |
|
0 |
|
|
г) E = ρr/(3ε0) при r 6 R; E = ρR |
/(3ε0r |
д) E = ρr/(2ε0) при r 6 R; E = |
|||||||||
ρR2/(2ε0r) при r > R; |
е) E = ρx/ε0 при x 6 h/2 (x — расстояние от центральной плоскости |
||||||||||
пластины); E = ρh/(2ε0) при x > h/2.
322
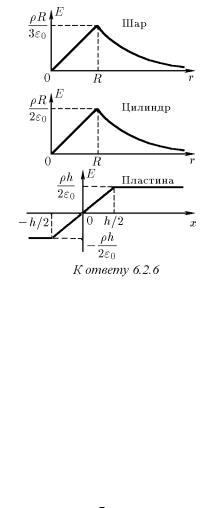
6.2.7. а) ρ = 2E0ε0/r; б) ρ = E0ε0/r. |
|
|
|
6.2.8 . Сила, действующая на выделенную грань куба, F = σ |
En ds, где |
En ds — поток |
|
остальными пятью гранями |
. |
||
через эту грань напряженности электрического поля, создаваемый R |
R |
|
|
В качестве замкнутой поверхности построим куб, немного б´ольший данного. Тогда все шесть заряженных граней дают поток напряженности электрического поля через все шесть сторон построенной поверхности Φ = q/ε0 = 6σl2/ε0, а через одну грань Φ0 = σl2/ε0. Но
Φ0 = En dS + σl2/(2ε0), |
|||||||
|
Z от пяти |
от выделенной |
|||||
|
граней |
|
грани |
||||
следовательно, |
|
|
|
|
|
|
|
Z |
|
σl2 |
− |
σl2 |
|
σl2 |
|
En ds = |
|
|
= |
|
. |
||
ε0 |
2ε0 |
2ε0 |
|||||
Значит, сила F = σ2l2/(2ε0). Аналогично рассуждая, для тетраэдра получим
F= √3 σ2l2/(8ε0).
6.2.9.Между плоскостями E1 = σ/ε0, E2 = 0. Вне плоскостей E10 = 0, E20 = σ/ε0.
6.2.10.E1 = (σ/ε0) sin(α/2), E2 = (σ/ε0) cos(α/2).
6.2.11.Eмакс = ρh/ε0.
6.2.12.EA = ρh/(6ε0), EB = ρh/(3ε0), E(r) = ρr/(3ε0).
6.2.13 . В любой точке внутри полости напряженность поля направлена вдоль прямой,
соединяющей центры шара и полости, и E = ρl/(3ε0). |
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
ρ |
|
r3 |
ρ |
|
|
r3 |
|
|
|
||||
Вне полости E = |
|
|
x + |
|
|
|
при 0 < x < l − r; E = |
|
x − |
|
|
|
|
при l + r < |
|||||
3ε0 |
(l |
− |
x)2 |
3ε0 |
(x |
− |
l)2 |
||||||||||||
|
ρ |
|
R2 |
|
r2 |
|
|
|
|
|
|
|
|
|
|||||
x < R; E = |
|
|
|
− |
|
|
|
при x > R. |
|
|
|
|
|
|
|
||||
3ε0 |
x2 |
(x − l)2 |
|
|
|
|
|
|
|
||||||||||
6.2.14 . а. E = ρl/(3ε0). |
б. σ = 3ε0E cos α, где α — угол между направлением поля и |
||||||||||||||||||
радиусом, проведенным в точку на сфере. σмакс = 3ε0E. |
|
|
|
|
|
|
|
||||||||||||


6.3.31 . ϕ = q/(4πε0L). 6.3.32 . Q = −qR/L.
6.3.33. Увеличится на F = Qq/(4πε0L2) при L > R; не изменится при L < R.
6.3.35.h = 3q2R2/(16π2ε0ρgr6), где h отсчитывается от центра шара.
6.3.36.Q0 = qQ/(Q − q).
6.3.39.Увеличится в три раза.
6.3.40.C = 4πε0R.
§ 6.4. Конденсаторы
6.4.2.а. Увеличилась в четыре раза. б. Уменьшится в два раза; уменьшится вn раз.
6.4.3.а. C = ε0S/d. б. C = 5,3 см = 5,9 пФ.
6.4.4. а. Увеличится в полтора раза. б. Увеличится в 1 + S0/(2S) раз. в. Не изменится.
6.4.5. C = 4πε0 |
R1R2 |
. |
|
|
|
|
|
6.4.6. C = 4πε0 |
R1 − R2 |
− R0 |
(R0 − d)) − |
1 |
|||
R1 |
− R2 |
. |
|||||
|
1 |
1 |
|
|
d |
|
|
6.4.7 . C = 2πε0l/ ln(R2/R1).
|
6.4.8 . C = |
ε0al |
1 + |
ld |
. |
||
|
d |
2πR2 |
|||||
|
|
|
|
|
|
||
|
6.4.9. а. C = C1C2/(C1 + C2), C = C1 + C2. б. C0 = 4C/3. в. C0 = 7C/5. |
||||||
г. C0 |
√ |
|
− 1)C/2. д. C0 = 6C/5. |
||||
= ( |
5 |
||||||
6.4.10.q = ±ε0SEa .
6.4.11.V = d + a (V1 + V2).
6.4.12 . а. Увеличится в полтора раза. б. Увеличится в два раза.
6.4.13.q = qx/d.
|
V |
= |
Cd + 2ε S |
|
4n |
6.4.14 . |
|
0 |
. |
||
V0 |
Cd + ε0S |
6.4.15.F = 4,4 · 10−2 Н. Нет.
6.4.16.Увеличится в k раз. Увеличится в n2 раз.
6.4.17.а) W = 4,4 мДж; б) W = 2πε0r1r2V 2/(r2 − r1); в) W = πε0lV 2/[ln(r2/r1)].
6.4.18. а. A = Q2d/(2ε |
S). |
б. A = Q2dx/[2ε |
a2(a |
− |
x)]. в. A |
а |
= Q2d/(4ε |
A); A |
б |
= |
|
Q2dx/(2ε0a3). |
0 |
|
0 |
|
|
0 |
|
|
|||
§ 6.5. Электрическое давление. Энергия электрического поля
6.5.1.а. F = σ2S/(2ε0). P = σ2/(2ε0). б. σ = ε0E. P = ε0E2/2 (в СИ), P = E2/(8π) (в СГС). в. P = 4,325 Па, σ = 8,85 мкКл/м2.
6.5.2.Уменьшится в 1 + Q2/(2P0ε0S2) раз.
6.5.3.По теореме Гаусса определим поверхностную плотность заряда на границе раздела полей: σ = ε0E. Используя принцип суперпозиции,
E0 − σ/(2ε0) = E, E0 + σ/(2ε0) = 2E,
найдем напряженность внешнего поля: E0 = 3E/2. Сила, которая действует на заряд, приходящийся на единицу площади поверхности раздела полей, т. е. давление со стороны внешнего поля P = E0σ = 3ε0E2/2. Для полей E и −2E, аналогично рассуждая, получим σ = −3ε0E и E0 = −E/2. Таким образом, во втором случае поверхностная плотность заряда в три раза больше, но напряженность внешнего поля в три раза меньше. Поэтому электрическое давление будет тем же: P = E0σ = 3ε0E2/2.
6.5.4.P = ρ2h2/(2ε0).
6.5.5.P = Q2/(32π2ε0R4) (см. решение задачи 6.5.3).
6.5.6.P = ε0R√2V 2/[2r2(R − r)2].
|
|
6.5.7. ρ = 2πR 2ε0P . |
|
|
|
||||
|
|
6.5.8 . а. F1 = qσ/(4ε0), F2 = √ |
|
qσ/(8ε0), F3 |
= √ |
|
qσ/(16ε0); E1 = σ/(4ε0), E2 = |
||
2 |
3 |
||||||||
√ |
|
σ/(8ε0), E3 = √ |
|
σ/(16ε0). б. E = Rρ/(4ε0). |
|
|
|
||
2 |
3 |
|
|
|
|||||
|
|
6.5.9 . F = Q2(R2 − h2)/(32πε0R4); q = −Q/2. |
|
|
|
||||
21 |
325 |
||||||||