
Замараев - часть 3
.pdfли после такой флуктуации система стремится возвратиться в исходное стационарное состояние, то она является устойчивой по Ляпунову. В противном случае, систему называют
неустойчивой.
Рассмотрим эволюцию системы (6.99) при небольшом от-
клонении от стационарного состояния
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Cx1 = |
C |
x1 + Dx1 , Cx2 = |
C |
x2 + Dx2 , |
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
причем Dx1,Dx2 << |
|
|
|
x1 , |
|
|
x2 : |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
C |
C |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
ìdC |
|
|
|
|
|
|
|
|
dD |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
ï |
|
x1 |
= |
|
|
|
|
|
x1 |
|
= k1CA |
(Cx1 + Dx1 )- k2 (Cx1 |
+ Dx1 )× (Cx2 + Dx2 ), |
|
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
ï |
dt |
|
|
|
|
|
|
|
|
|
|
dt |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
í |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
( |
|
|
|
|
|
|
|
|
|
)× |
( |
|
|
|
|
|
|
|
|
|
|
|
)- k |
|
( |
|
|
|
|
). |
|
|||||||
|
|
ï |
dCx2 |
|
= |
dDx2 |
= k |
|
|
|
|
+ D |
|
|
|
+ D |
|
|
|
|
+ D |
|
||||||||||||||||||||||||||||||||||||||
|
|
2 |
C |
x1 |
C |
x2 |
3 |
C |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
ï |
dt |
|
|
|
|
|
|
|
|
|
|
dt |
|
|
|
|
|
|
|
|
|
|
|
x1 |
|
|
|
|
|
x2 |
|
|
|
|
|
|
x2 |
|
x2 |
|
|
|||||||||||||||||
|
|
î |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
Раскрываем скобки и учитываем систему уравнений (6.100) |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ß |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ìdDx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
= k CACx |
- k2Cx |
|
Cx |
|
|
+ k1CADx - k2Cx Dx - k2Cx Dx + k2Dx Dx , |
||||||||||||||||||||||||||||||||||||||||||||||||||||
ï |
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
dt |
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
ï |
|
|
144424443 |
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
2 |
|
1 |
|
|
|
|
1 |
2 |
|
1 |
2 |
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
1 |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
í |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dDx2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
ï |
|
= k |
|
|
|
- k |
|
+ k |
|
D + k |
|
D - k D - k D D . |
|
|||||||||||||||||||||||||||||||||||||||||||||||
|
C |
C |
C |
C |
C |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
ï |
dt |
|
|
144424443 |
|
|
|
|
|
2 x2 |
|
x1 |
|
|
2 x1 |
|
|
x2 |
3 x2 |
|
|
2 x1 x2 |
|
|||||||||||||||||||||||||||||||||||||
ï |
|
|
|
|
|
2 x1 |
|
|
|
x |
|
|
|
3 x2 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
î |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Линеаризуем уравнения, т. е. воспользуемся малостью от- клонений и пренебрежем квадратичными членами по Dxi :
ìdDx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
= k1CADx |
- k2Cx Dx |
- k2Cx |
|
Dx , |
||||||||||
ï |
|
|
|
|||||||||||||
dt |
|
|
||||||||||||||
ï |
|
|
|
|
|
1 |
2 |
1 |
|
|
1 |
2 |
||||
í |
dDx2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ï |
|
= k |
|
D + k |
|
D - k D . |
||||||||||
|
C |
C |
||||||||||||||
ï |
|
|
|
|||||||||||||
dt |
|
|
2 x2 |
x1 |
2 x1 |
x2 |
3 x2 |
|||||||||
î |
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Подставим стационарные концентрации промежуточных реа- гентов из выражений (6.101):
58
ìdDx |
1 |
|
= -k3Dx2 , |
|||
ï |
|
|
||||
|
|
|||||
ï |
dt |
|
|
|
|
(6.102) |
í |
|
|
|
|
||
ï |
dDx2 |
|
= k C |
D |
. |
|
|
|
|||||
ï |
dt |
|
|
1 A |
|
x1 |
î |
|
|
|
|
|
|
Это система линейных дифференциальных уравнений, решение которой аналогично рассмотренному в разд. 3.3. Ее
характеристическое уравнение
0 - l |
- k3 |
|
|
C |
|
= 0 |
|
2 |
|
||||
|
|
|
= l + k k |
A |
||
k1CA |
|
0 - l |
1 3 |
|
|
|
|
|
|
|
|
имеет два мнимых собственных значения (поскольку констан- ты скорости и концентрации неотрицательны)
l = i
 k1k3CA = iw , l = -i
k1k3CA = iw , l = -i
 k1k3CA = -iw.
k1k3CA = -iw.
Так как мы оперируем физическими величинами – концентра- циями, решение системы должно быть действительным:
Dx1 = a00ei×w×t + a01e-i×w×t = a'00 cos(wt)+ a'01 sin(wt),
Dx2 = a10ei×w×t + a11e-i×w×t = a'10 cos(wt)+ a'11 sin(wt).
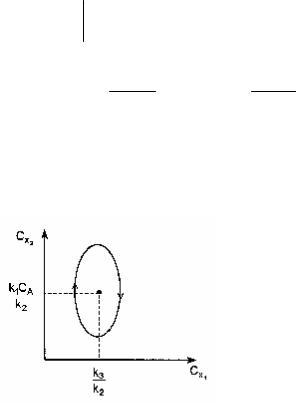
|
Мы |
получили |
удиви- |
|||
|
тельный |
результат |
– |
|||
|
выведенная |
из |
состоя- |
|||
|
ния |
покоя |
система |
не |
||
|
возвращается назад, |
а |
||||
|
начинает |
|
осциллиро- |
|||
|
вать |
около |
стационар- |
|||
|
ной точки (рис. 6.15). |
|
||||
|
Таким образом, ал- |
|||||
|
горитм анализа |
устой- |
||||
|
чивости |
стационарного |
||||
Рис. 6.15. Осцилляции концентраций реа- |
состояния |
выглядит |
||||
так: |
|
|
|
|
|
|
гентов x1 и х2 вокруг стационарного со- |
|
|
|
|
|
|
стояния
59
1)находим стационарные решения;
2)рассматриваем уравнения для малых отклонений вбли- зи стационарного состояния, т. е. линеаризуем систему, от- брасывая слагаемые, квадратичные по отклонениям от ста- ционарного состояния;
3)находим собственные значения li для полученной ли- нейной системы дифференциальных уравнений;
4)если все действительные части собственных значений
Re(li) < 0, то стационарное состояние устойчиво, в противном случае возможны осцилляции;
5) повторяем пп. 2–4 для каждого стационарного состоя- ния.
Полученные из анализа устойчивости заключения о пове-
дении системы вблизи стационарного состояния справедливы только для малой окрестности стационарной точки. Хотя не- устойчивость стационарного состояния (или нескольких ста- ционарных состояний в сложных системах) является необхо- димым условием возникновения автоколебаний, точно отве- тить на вопрос, реализуется ли в рассматриваемом случае колебательный режим протекания реакции, можно только изучив поведение системы на всей фазовой плоскости. Для приведенной схемы Лотки–Вольтерра достаточно легко полу- чить уравнения, связывающие между собой Cx1 и Cx2 . Для
этого поделим уравнения (6.99) друг на друга
dCx |
= |
(k1CA - k2Cx )× Cx |
, |
||||||
dC |
|
1 |
(k C - k |
|
)× C |
|
1 |
||
|
|
|
|
|
2 |
|
|
||
|
x |
2 |
|
2 x |
3 |
|
x |
2 |
|
|
|
|
1 |
|
|
|
|
||
разделим переменные и проинтегрируем:
(k2Cx1 - k3 )× dCx1 |
= |
|
(k1CA - k2Cx2 )× dCx2 |
, |
|
|
|||
Cx1 |
|
Cx2 |
||
|
|
ß |
|
|
k2Cx1 - k3 ln(Cx1 ) = k1CA ln(Cx2 )- k2Cx2 + const . (6.103)
60
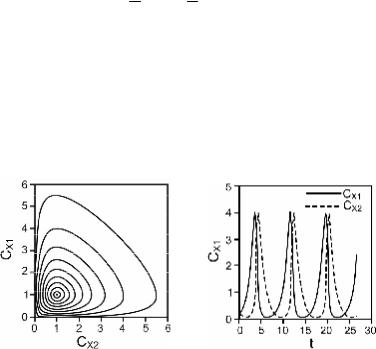
На рис. 6.16, а приведено семейство фазовых кривых, рас- считанных по формуле (6.103) для системы, имеющей ста-
ционарное состояние Cx1 = 1, Cx2 = 1. На рис. 6.16, б для той же системы показаны осцилляции концентраций Cx1 , Cx2 во времени при начальном условии Cx1 = 0.2, Cx1 = 0.2 , полу-
ченные численным интегрированием (6.99). Как следует из рис. 6.16, поведение системы вдали от стационарной точки качественно совпадает с ранее полученными результатами: фазовые траектории представляют собой ряд непересекаю- щихся замкнутых кривых, соответствующих колебательному режиму реакции.
Рис. 6.16. Колебательный режим реакции в схеме Лотки–Вольтерра
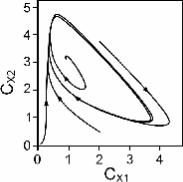
Для более сложных систем возможны множественные ста- ционарные состояния, устойчивые либо неустойчивые, а так- же другие стационарные решения, например предельные циклы. На рис. 6.17 изображена фазовая плоскость решений для кинетической схемы, предложенной Лефевром:
A ¾¾® X1,
X1 ¾¾® X2,
(6.104)
2X1 +X2 ¾¾® 3X1, X1 ¾¾® F.
61
|
Модели такого типа на- |
||
|
ходят широкое применение |
||
|
при |
анализе |
биохимиче- |
|
ских |
процессов, поскольку |
|
|
позволяют качественно ин- |
||
|
терпретировать |
экспери- |
|
|
ментальные данные. При |
||
|
определенных |
значениях |
|
|
параметров данная кине- |
||
|
тическая схема имеет одну |
||
|
неустойчивую |
стационар- |
|
|
ную точку и один устойчи- |
||
Рис. 6.17. Колебательный режим |
вый предельный цикл. Это |
||
реакции в схеме Лефевра |
означает, что |
независимо |
|
от начальных условий при наблюдении в течение некоторого промежутка времени опи- сываемая схемой (6.104) система перейдет к единственно возможному колебательному режиму реакции со строго опре- деленными периодом и амплитудой колебаний промежуточ- ных компонентов Х1 и Х2.
62
Глава 7 Цепные реакции
Цепные реакции – это химические процессы, в которых превращение исходных веществ в конечные продукты осуществляется путем регулярного чередования нескольких реакций с участием свободных радикалов (или атомов), идущих с сохранением свободной валентности.
Свободные радикалы, участвующие в цепной реакции, час- то называют активными центрами цепной реакции.
По цепному механизму протекает ряд важных классов хи- мических реакций:
1)окисление молекулярным кислородом, в том числе го- рение;
2)галоидирование многих соединений;
3)некоторые реакции термического распада, например пи- ролиз углеводородов;
4)многие реакции полимеризации.
Любая цепная реакция обязательно включает три основ- ные стадии: зарождение, продолжение и обрыв цепи.
Зарождением (инициированием) цепей называется ста-
дия цепной реакции, в которой образуются свободные ради- калы из валентно-насыщенных молекул исходных веществ.
Реакциями продолжения цепей называются стадии цеп-
ной реакции, идущие с сохранением свободной валентности и приводящие к расходованию исходных веществ и образова- нию продуктов реакции.
Обрывом цепей называются стадии цепной реакции, при- водящие к исчезновению свободной валентности.
В некоторых цепных реакциях наряду с элементарными стадиями зарождения, продолжения и обрыва цепей проис-
ходят процессы с участием активных центров или стабильных продуктов реакции, идущие с увеличением числа активных центров – атомов и свободных радикалов.
Элементарная стадия цепной реакции, в которой превра- щение активных промежуточных частиц или реакционноспо-
63
собных продуктов реакции приводит к увеличению числа сво- бодных радикалов или атомов, называется разветвлением цепи.
Цепные реакции, в которых отсутствует стадия разветвле-
ния цепей, называются неразветвленными цепными ре-
акциями. Цепные реакции, в которых имеется стадия раз-
ветвления, называются разветвленными цепными реакциями.
§ 7.1. Неразветвленные цепные реакции
Классическим примером неразветвленных цепных реакций является хлорирование водорода.
Простая бимолекулярная реакция
H2 + Cl2 ¾¾® 2HCl
не идет из-за запрета симметрии (отсутствует перекрывание между HOMO и LUMO орбиталями реагентов). Основным ка- налом реакции является превращение по следующему нераз- ветвленному цепному механизму:
|
|
0. |
|
Wo |
∙ |
|
|
|
|
|
|
||
|
|
Cl2 (+M) ¾¾¾® 2 Cl (+M) |
||||
|
ì |
|
∙ |
k |
∙ |
ü |
Звено |
ï 1. |
Cl + H2 |
1 |
|
ï |
|
¾¾® HCl + H |
||||||
цепи |
í |
|
∙ |
k |
∙ |
ý |
ï |
2. |
H + Cl |
|
|
||
|
¾¾2 ® HCl + Cl ï |
|||||
|
î |
|
2 |
|
|
þ |
Линейный |
ì |
3. |
∙ |
|
|
ü |
ï |
Cl + стенка ¾¾® гибельï |
|||||
обрыв |
í |
|
∙ |
|
|
ý |
ï |
4. |
|
|
|
ï |
|
|
î |
H + стенка ¾¾® гибель þ |
||||
–стадия зарож- дения (иниции- рования) цепи;
–стадия продол- жения цепи;
–стадия обрыва цепи,
|
ì |
|
∙ |
¾¾® Cl2 |
|
ü |
|
|
ï 5. |
2Cl (+M) |
(+M) |
ï |
|
||
Квадратичный |
ï |
|
∙ |
¾¾® H2 |
|
ï |
– стадия обрыва |
í 6. |
2H (+M) |
(+M) |
ý |
||||
обрыв |
ï |
|
∙ ∙ |
|
|
ï |
цепи. |
|
7. |
H + Cl (+M) ¾¾® |
|
|
|||
|
ï |
HCl (+M)ï |
|
||||
|
î |
|
|
|
|
þ |
|
64

7.1.1. Реакции зарождения цепи
Примеры:
|
∙ |
|
|
|
|
|
|
1) |
C2H5I ¾¾® C2 H5 + I∙ – гомолитическая диссоциация с |
||||||
разрывом наименее |
прочной |
связи C - I (D |
» 210– |
||||
–230 кДж / моль). Энергия активации E » D; |
|
||||||
|
Cl2 + стенка ¾¾® |
∙ |
|
|
|
||
2) |
Cl + Clадс |
– |
гетерогенная |
реакция |
|||
диссоциации; |
∙ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3) Cl2 + hn ¾¾® 2 Cl |
|
– инициирование светом; |
|
||||
4) Hg + hn ¾¾® Hg * , |
|
ü |
– фотосенсибилизиро- |
||||
|
ï |
||||||
Hg * + C H ¾¾® |
∙ |
|
∙ |
ý |
ванное инициирование; |
||
C |
|
H + H + Hgï |
|||||
|
3 8 |
|
3 |
7 |
þ |
|
|
5) распад инициатора, вводимого в систему в виде добавки:
Ph |
|
C |
|
O |
|
O |
|
C |
|
Ph |
|
2 PhC |
O |
||
|
|
|
|
|
|
O |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
O |
|
O |
|
|
|
|
|
||||||
или
∙
NOCl ¾¾® NO + Cl ;
6) реакции переноса электрона с участием инициатора:
∙
RH + CoIII ¾¾® R + CoII + H+ ; 7) инициирование в бимолекулярных реакциях:
∙ ∙
RH + O2 ¾¾® R + HO2 .
Энергия активации E = D(R - H) - D(OH) ∙ < D(R − H) .
HO2
7.1.2. Реакции продолжения цепи
Примеры последовательности реакций продолжения, об-
разующих звено цепи:
∙ |
∙ |
1) R + O2 |
¾¾® RO2 , |
65
∙ |
∙ |
RO2 |
+ RH ¾¾® ROOH + R . |
Такие звенья реализуются в реакциях окисления углеводоро-
∙
дов и альдегидов (R – радикал углеводорода или альдегида).
|
∙ |
+ O2 |
¾¾® |
∙ |
||
2) CH3 |
CH3O O , |
|||||
|
|
∙ |
∙ |
|
|
|
|
CH3OO ¾¾® CH2OOH , |
|||||
|
∙ |
|
|
|
∙ |
|
|
CH2OOH |
¾¾® |
CH2O + OH , |
|||
|
∙ |
|
|
|
∙ |
|
|
OH |
+ CH4 |
¾¾® |
H2O + CH3 . |
||
|
|
|
|
|
|
|
Такое звено реализуется при окислении (горении) метана.
∙ |
∙ |
3) RH + Hal ¾¾® HHal + R , |
|
∙ |
∙ |
R + Hal2 |
¾¾® RHal + Hal . |
Такие звенья реализуются при галогенировании углеводоро- дов и водорода.
∙ |
∙ |
4) Cl + C2H4 |
¾¾® C2 H4Cl , |
∙ |
∙ |
C2 H4Cl + Cl2 ¾¾® C2H4Cl2 + Cl.
Такого рода звенья реализуются при галогенировании оле- финов.
|
∙ |
|
|
∙ |
5) CH3 |
+ CH3CHO ¾¾® CH4 + CH3CO , |
|||
|
|
∙ |
∙ |
+ CO . |
|
CH3 CO ¾¾® |
CH3 |
||
Такого рода звенья реализуются при термическом распаде карбонильных соединений.
∙ |
+ C2H6 ¾¾® |
∙ |
+ H2 , |
|
6) H |
C2H5 |
|||
∙ |
|
|
∙ |
|
C2 H5 |
¾¾® C2H4 + H . |
|||
66

Такого рода звенья реализуются при термическом распаде углеводородов (пиролизе).
|
∙ |
+ FeIII |
¾¾® H+ + O2 + FeII , |
||
7) HO2 |
|||||
|
|
|
|
|
∙ |
|
FeII |
+ H2O2 |
¾¾® FeIII + OH− + OH , |
||
|
∙ |
|
|
∙ |
|
|
OH |
+ H2O2 |
¾¾® H2O + HO2 . |
||
|
|
|
|
|
|
Такого рода звенья с участием соединений переходного ме-
талла реализуются в так называемых цепнокаталитических процессах. В этих процессах соединения металлов являются катализатором, обеспечивающим возможность реализации цепного механизма.
В результате последовательности реакций продолжения, образующих звено цепи, вновь возникает свободный радикал, начавший эту последовательность.
Важной характеристикой является время развития звена τзв. Если звено цепи представить в виде последовательности
реакций
∙ |
k1 |
∙ |
k2 |
∙ |
|
||
R1 |
|
|
R2 |
|
|
R1 , |
(7.1) |
A1 |
A2 |
||||||
|
|
|
|
|
|
∙ |
∙ |
то tзв будет равно сумме времени жизни радикалов R1 |
и R2 : |
||||||
tзв |
æ |
∙ |
ö |
æ |
∙ |
|
ö |
= t çR1 |
÷ + |
t çR |
2 |
÷ . |
|||
|
è |
|
ø |
è |
|
|
ø |
Времена жизни радикалов |
|
|
|
|
|
|
|
|||
æ ∙ |
|
ö |
−1 |
æ |
∙ |
|
ö |
= (k2 |
−1 |
, |
t çR |
1 |
÷ |
= (k1 ×CA1 ) |
и t çR |
2 |
÷ |
× CA2 ) |
|||
è |
|
ø |
|
è |
|
|
ø |
|
|
|
(7.2)
(7.3)
где CA1 и CA2 – концентрации насыщенных молекул, по реак-
циям с которыми гибнут радикалы.
Величины
a1 = k1 ×CA1 и a2 = k2 × CA2 |
(7.4) |
67
