Эконометрика. Тихомиров

Несложно заметить, что при наличии ошибок измерения у зависимой и независимых переменных эконометрическая модель может быть представлена в следующем виде:

где – вектор ошибки истинной модели; u – вектор ошибки измерений зависимой переменной, V – матрица ошибок измерений независимых переменных.

Даже при вполне естественных предположениях о взаимной независимости ошибок , u и V, истинных значений переменных хi и этих ошибок, используя примененные в двух других случаях подходы, можно показать, что:

а) дисперсия такой модели увеличивается по сравнению с моделью,

исходные данные которой измерены без ошибок;

б) использование обычного МНК дает смещенные оценки ее параметров.

В частности, заметим, что дисперсия модели (10.12) при этих предположениях определяется следующим выражением:

а величины смещения при конечном Т и при Т определены выражениями

(10.9) и (10.10) соответственно.

Как следует из полученных выше результатов, наибольшие трудности при построении эконометрических моделей с ошибками в исходной информации на основе обычного МНК возникают в случае наличия ошибок измерений у независимых переменных. Они связаны с необходимостью устранения смещения в получаемых оценках. Основным методом, который получил достаточно убедительное теоретическое обоснование и широкое

переменных, определяющих тенденции развития фактора хi, а t – фактор времени.

В отсутствии таких “сглаженных переменных”, удовлетворительные

результаты можно получить, используя в качестве инструментальных

типа 1,2,3,..., характеризующие порядковые номера уровней этих переменных в их ранжированном ряду. Иными словами, 1 присваивается значению zi ,

всех оставшихся значений переменных и т. д.

10.2. Модели с фиктивными независимыми переменными

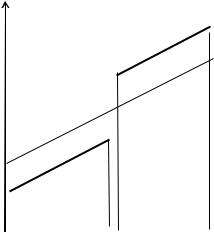
Фиктивные переменные вводятся в эконометрическую модель обычно с целью учета воздействия качественных аспектов на закономерности развития рассматриваемых процессов. К таким аспектам, например, относится различие в условиях развития процессов, предопределивших разницу их уровней в разные периоды времени при сохранении их общих тенденций (см.

рис. 10.1).

На рис. 10.1 показано, что в период (0, T1) для развития процесса была характерна тенденция (1), а в период (T1+1, T2) – тенденция (2) (например, до дефолта и после дефолта, если дефолт не повлиял на характер самой тенденции).

При этом динамические характеристики этих тенденций (темпы роста,

первая производная) совпадают.

у

2

1

t

Рис. 10.1. Пример различий в условиях развития процесса

Если не принимать во внимание отмеченные различия и попытаться построить единую, обобщенную модель для периода (0, T2), то , очевидно,

что ее уравнение будет соответствовать пунктирной линии, проходящей между сплошными линиями, характеризующими реальные тенденции процесса в рассматриваемых периодах.

Из рис. (10.1), в частности, также вытекает, что, если эконометрическая модель строится только на основе информации первого периода, то ее уравнение будет иметь следующий вид:

а, если только по информации второго периода, то

Отличаются эти выражения, если не принимать во внимание возможные различия в их ошибках, только величиной свободного коэффициента, т. е. 0.

Если ввести фиктивную переменную x0i, i=1,2, со следующими свойствами:

1, в первый период;

х01=

0, во второй период;

0, в первый период;

х02=

1, во второй период;

то выражения (10.26) и (10.27) могут быть объединены в рамках одной модели следующего вида:

Матрица исходных данных для такой модели будет иметь следующий вид:

Xit – матрица значений основных независимых переменных модели, i=1,2,...,

п; t=1,2,....,Т2.

Очевидно, что в этом случае условное математическое ожидание переменной у будет иметь следующий вид:

M[y/ х1 1, х2 0, Xit]= 01 f( ,x) для t=1,2,..., Т1;

и

M[y/ х1 0, х2 1, Xit]= 02 f( ,x) для t= Т1+1,..., Т2;

Заметим, что для рассматриваемого случая может быть предложена и другая модификация модели (10.28), например, с одной фиктивной

переменной (пусть х02), но содержащая свободный член. Ее вид определен следующим уравнением:

и матрица исходных данных для такой модели примет следующий вид:

Вместе с тем, несложно увидеть, что введение свободного члена в модели

(10.28) невозможно, поскольку следствием этого является появление единичного столбца в матрице (10.29), что влечет за собой ее необратимость,

поскольку единичный столбец представляет собой линейную комбинацию столбцов значений фиктивных переменных.

Модели типа (10.28) и (10.30) легко могут быть сформированы и на случай большего числа групп фиктивных переменных. Они могут выражать определенные временные периоды (например, с целью учета сезонности),

статус объекта и т. п. В частности, в рассматриваемой в первой главе модели заболеваемости такие переменные могут выражать время года (весна, лето,

осень зима), половозрастную группу населения (взрослые и дети, мужчины и женщины). В этом случае вводятся две группы переменных – временная и половозрастная (всего восемь). Обозначим эти переменные как s1, s2, s3, s4; q1, q2, q3, q4. При этом

1, если наблюдения относятся к i-му времени года, i=1,2,3,4;

si=

0, в остальных случаях;

1, если наблюдения относятся к j-й половозрастной группе j=1,2,3,4;

qj=

0, в остальных случаях;

Тогда эконометрическая модель типа (10.28), описывающая заболеваемость в регионе в зависимости от условий жизнедеятельности,

времени года и половозрастной группы индивидуума, может быть представлена в следующем виде:

где хit – факторы жизнедеятельности.

Оставление свободного члена в модели заболеваемости, как и в модели

(10.30), приведет к уменьшению числа ее фиктивных переменных. В этом случае выражение (10.32) преобразуется к виду:

При этом для первого временного сезона и первой половозрастной группы получим 0= 01+ 01.

Заметим, что модели типа (10.32) и (10.33) корректны, если все группы населения одинаково реагируют на изменение условий жизнедеятельности и,

кроме того, заболеваемость характеризуется параллельными сдвигами со сменой времени года.