1 семестр / molekulyarka_i_mekhanika_fizika_2015-16 / Лаб. раб. №1.8 изм 12.12

ЛАБОРАТОРНАЯ РАБОТА № 1.8

«ИЗУЧЕНИЕ ЗАКОНОВ СОХРАНЕНИЯ ЭНЕРГИИ И

МОМЕНТА ИМПУЛЬСА С ПОМОЩЬЮ БАЛЛИСТИЧЕСКОГО МАЯТНИКА»

I.Цель работы: ознакомление с принципом работы баллистического крутильного маятника; определение скорости полета пули, попавшей в него.

II.Описание установки.

Общий вид баллистического крутильного маятника представлен на рисунке. К кронштейну 1 прикреплены: стреляющее устройство 2, прозрачный экран с нанесенной на него угловой шкалой 3 и фотоэлектрический датчик 4. Маятник состоит из двух мисочек, наполненных пластилином 5, двух перемещаемых грузов 6, двух стержней 7 и заслонки 8.

Если освободить пулю от стреляющего устройства, то она вклеится в пластилин, находящийся в мисочках крутильного маятника, и вызовет отклонение последнего на некоторый угол от положения равновесия. Кинетическая энергия маятника, полученная им от пули, постепенно будет переходить в потенциальную энергию упругой деформации закручивающейся нити.

Затем начнется процесс перехода потенциальной энергии в кинетическую и т.д. Маятник будет совершать гармонические крутильные колебания, период которых значительно больше времени соударения.

Угол отклонения маятника считывают с угловой шкалы 3. Число колебаний и время определяется миллисекундомером 9.

III.Методика измерений и расчетные формулы

Систему пуля - маятник можно считать замкнутой. Применим к ней закон сохранения момента импульса:

,

где и - масса и скорость пули соответственно; r - расстояние от оси вращения маятника до центра масс пули в месте ее вклеивания; J_n - момент инерции пули относительно оси вращения маятника; J - момент инерции маятника при некотором расположении грузов на нем; - начальная угловая скорость маятника.

Поскольку J_n << J, то

. (1)

Из (1) следует, что для определения скорости пули необходимо найти момент инерции и начальную угловую скорость маятника, т.к. величины m и r могут быть непосредственно измерены.

Дня определения воспользуемся законом сохранения механической энергии и основным законом динамики для вращательного движения.

Маятник будет совершать колебания под действием упругого момента нити, пропорционального углу поворота маятника α:

М = -,

где k - коэффициент пропорциональности (модуль кручения). Знак "-" указывает на то, что вектор момента силы направлен в сторону, противоположную направлению вектора отклонения маятника.

Элементарная работа против сил упругости по закручиванию нити на малый угол равна

.

После интегрирования получаем, что .

Если пренебречь незначительными потерями на трение, то можно записать:

или , (2)

где - максимальный угол отклонения маятника от положения равновесия.

По закону динамики для вращательного движения

или .

Частным решением этого уравнения является

в чем можно убедиться непосредственной подстановкой.

Величина - в последнем выражении является циклической частотой колебаний, которая по определению равна .

Таким образом, маятник будет совершать гармонические колебания с периодом

. (3)

Подставив в формулу (3) выражение для из формулы (2), получим следующее выражение для начальной угловой скорости маятника:

. (4)

Если на стержне маятника закреплены 2 груза, причем расстояние R₁, от оси маятника до центра масс каждого груза значительно больше размеров груза, то момент инерции системы будет равен

, (5)

где m₁ - масса одного груза; J₀ - момент инерции маятника без грузов.

При изменении положения грузов момент инерции изменится и будет равен

, (6)

где R₂- новое расстояние от центра масс каждого груза до оси вращения.

Исключив J₀ из формул (5) и (6), получим

. (7)

Теперь воспользуемся формулой (3), переписанной в виде

. (8)

Подставив выражение (7) в (8), получим

. (9)

Коэффициент k можно выразить из формулы (3):

.

Подставив k в равенство (9), получим

(10)

где Т₁ и Т₂ - периоды колебаний маятника для расстояний R₁ и R₂ соответственно.

Аналогично можно получить формулу

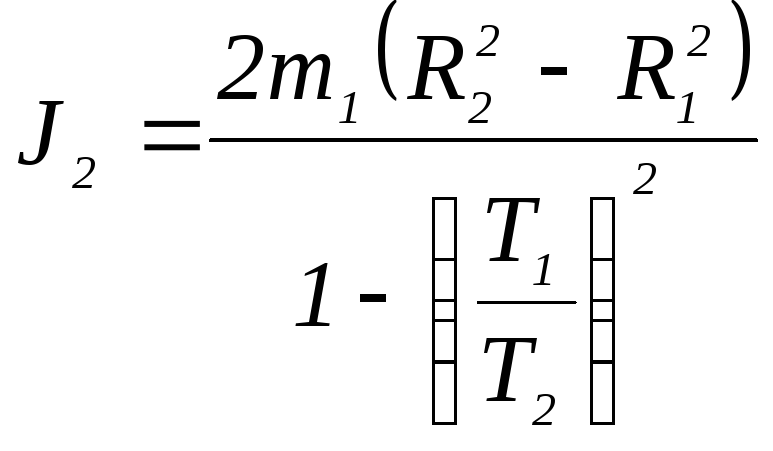. (11)

IV.Порядок выполнения работы

1. Максимально приблизить грузы к оси маятника (R₁=R_min),но так, чтобы R₁ было существенно больше размера груза. Измерить R₁.

2. Обнулить, если это необходимо, маятник: черта на мисочке должна показывать угол = 0.

3. Выстрелить пулю из стреляющего устройства и измерить максимальный угол отклонения маятника от положения равновесия, а также расстояние от оси вращения до места вклеивания пули r. Опыт повторить 3-5 раз.

4. Нажать кнопку "Сеть".

5. Отклонить рукой маятник на небольшой угол <<, нажать кнопку "Сброс" и отпустить маятник.

6. Измерить время t десяти колебаний: кнопку "Стоп" нажать в момент появления на счетчике периодов цифры "9".

7. Повторить измерения по п.п. 5, 6 не менее 5 раз.

8. Максимально отдалить грузы от оси колебаний (R₂ = R_max ). Измерить R₂.

9. Повторить п.п. 2-7.

V.Таблицы результатов измерений

1. Данные установки:

Масса груза: гр.

Масса пули: гр.

2. Измерение R,r 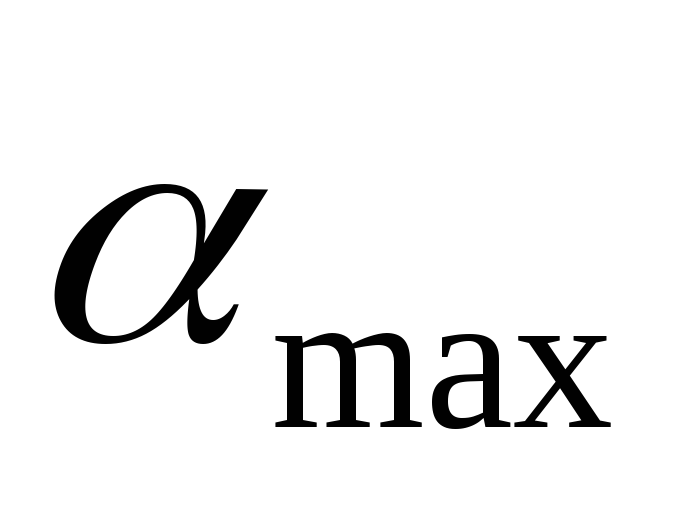(две серии опытов):

; ; .

Расчет: ; .

3. Измерение периода колебаний (две серии опытов).

.

Расчет: .

, .

Измерения занести в таблицу:

№	1-я серия опытов				2-я серия опытов
ср.			ср.				ср.

VI.Обработка результатов измерений

1. Используя формулу (4), определить угловую скорость для каждой серии опытов.

2. Рассчитать погрешность (для каждой серии опытов) по формуле

.

3. Записать окончательный результат в виде ; .

4. По формулам (10) и (11) рассчитать моменты инерции J₁ и J₂.

5. Рассчитать погрешность , используя формулу

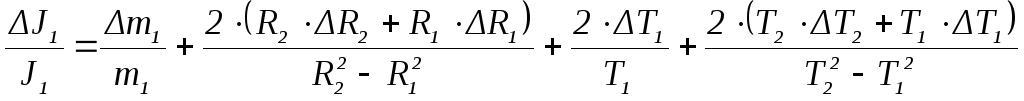
6. Записать окончательный результат в виде

; .

7. По формуле (1) рассчитать отдельно для каждой серии опытов скорость пули, используя данные расчета п.п. 3 и 6. Найти среднее значение.

8. Рассчитать погрешность (для каждой серии опытов) по формуле

.

Найти среднее значение .

9. Записать окончательный результат в виде

.

10. Сделать вывод о качестве проведенных опытов.

Контрольные вопросы

1 . Какие законы сохранения используются в данной работе? (Сформулировать их и указать условия применимости каждого).

2. Какие колебания называются гармоническими?

3. Что такое циклическая частота? период? От каких параметров колеблющейся системы они зависят?

4. Какие силы участвуют в создании гармонических колебаний крутильного маятника?

5. Как рассчитывается момент инерции системы?

6. Каким способом меняется момент инерции?

7. Объясните результаты Ваших опытов.

8. Поясните вывод формул (1), (4), (10) и (11).

3