Розрахункова таблиця для визначення значень функції f(t) по часткових інтервалах ряду (з використанням інженерного калькулятора

а = 2,52 тис. мото-г. в = 2,24)

Параметри	Граничні інтервали (t з урахуванням tзм) тис. мото-г.
	0...1	1...2	2...3	3...4	4...5	5...6
ТВі	1	2	3	4	5	6
ТВі/а	0,397	0,793	1,190	1,587	1,984	2,385
х = (ТВі/а)в	0,126	0,595	1,476	2,814	4,640	7,008
е-х	0,881	0,552	0,228	0,060	0,010	0,001
F(t) = 1- е-х	0,119	0,448	0,772	0,940	0,990	0,999

Значення F(t_і) (з табл. 3.7 або 3.9) використовують для побудови графіка теоретичної інтегральної функції в тих же осях координат, що і дослідна інтегральна функція розподілу на рис. 3.4, причому розрахункові значення F(t) відповідають верхнім границям часткових інтервалів (без поправки на t_зм).

3.8. Превірка відповідності між виробами теоретичним законом та емпіричним розподілом напрацювання виробу до відказу (клинових пасів або колінчастих валів) можна виконати з використанням одного з критеріїв згоди 1,4,5, який підтверджує або спростовує статистичну гіпотезу про вид вибраного теоретичного закону розподілу з прийнятим рівнем значущості . Звичайно, в технічних розрахунках приймають  рівним 0,1, тобто допускають тим самим в 10 випадках із 100 є можливість похибки першого роду, зв’язаної з риском відкинути вірну статистичну гіпотезу. Стосовно до завдання, що розглядається, пропонується проводити перевірку відповідності теоретичного та емпіричного розподілу по критерію згоди  О.М. Колмогорова 4,5. Для цього в табл. 3.10 визначають максимальне абсолютне значення різниці Д_max між емпіричною та теоретичною інтегральними функціями розподілу для окремих і-их часткових інтервалів, тобто 1, 4, 5:

(3.8)

Таблиця 3.10

Перевірка відповідності емпіричного та теоретичного розподілів напрацювання клинових пасів до першого відказу по критерію 

Границі часткових інтервалів, г	0...150	150...300	300...450	450...600	600...750	750...900
Верхня границя інтервала ТВі г.	150	300	450	600	750	900

Продовження таблиці 3.10

	-2,11	-1,05	0	1,05	2,11	3,16
(хі)	0,018	0,147	0,500	0,853	0,982	0,999
Fl(ti) = mi/N	0,025	0,125	0,475	0,900	0,975	1,000
D =	0,007	0,022	0,025	0,047	0,007	0,001

Як виходить з табл. 3.10 Д_max = 0,047. Тоді розрахункове значення критерія відповідно 1,4

Для  = 0,297 по додатку 8 знаходимо значення Р() = 1,0. Оскільки значення Р() більше прийнятого рівня значущості  = 0,1, то прийнята гіпотеза про можливість узгодження нормального розподілу з емпіричним розподілом напрацювання клинових пасів до першого відказу не відкидається. Теж можна сказати про відповідність теоретичного та емпіричного розподілів.

3.9. Інтервальна оцінка середнього напрацювання клиновихпасів до першого відказу на відміну від точкової оцінки (шляхом підрахунку середнього арифметичного значення) дозволяє одержати результат з наперед заданою вірогідністю або довірчою ймовірністю, яку в практичних розрахунках приймають рівною 0,8 або 0,9.

Нижню Т_н1 та верхню Т_В1 границі довірчого інтервала для середнього напрацювання визначають по рівнянню:

(3.9)

(3.10)

де t_(n) – квантиль розподілу t_ Стьюдента зі степенями n = N-1 вільності для статичної вибірки з N значень (додаток 9).

Для  = 0,9 та N = 40 квантиль t до (39)/= 0,206. Тоді в даному прикладі:

Т_Н1= 450 - 0,206 142,3 = 421,7 г.;

Т_В1 = 450 + 0,206 142,3 = 479,3 г.

Таким чином, з ймовірністю 0,9 можна затверджувати, що значення середнього напрацювання клинових пасів до першого відказу буде знаходитись в інтервалі від 421,7 г. і до 479,3 г.

При визначенні ймовірних границь розсіювання середнього значення показника надійності () для розподілу Вейбулла-Гнєденка необхідно користуватися рівняннями:

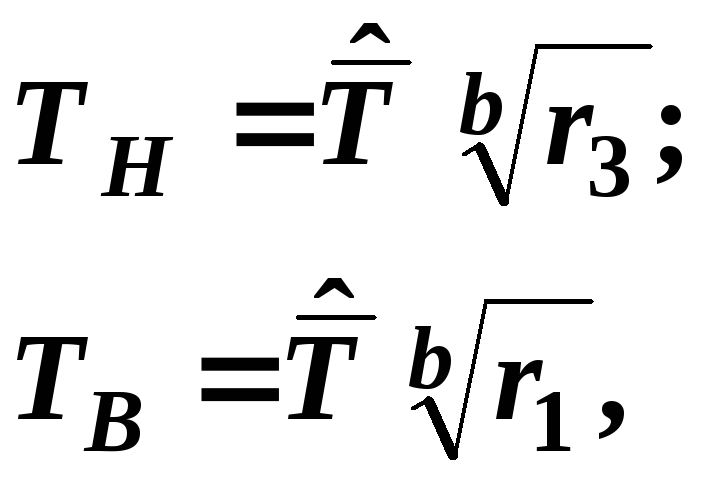(3.11)

де r₁ та r₂ – коефіцієнти Вейбулла, які визначаються по додатку 10 в залежності від  та N.

Програма розрахунку надійних границь по формулах (3.10) у випадку розподілу Вейбулла-Гнєденко наведені в табл. 3.11.

Таблиця 3.11