Програма розрахунку середнього значення

10 REM

15 DIN T(50), M(50)

20 S = 0

30 PRINT ROL INTERVALOW – N1”

40 INPUT NL

50 PRINT “OBEM VIBORKI NO”

60 INPUT NO

70 FOR J=1 TO N1

80 PRINT “SREDN I KOL “J” – GO INTERVALA”

90 INPUT T(J), N(J)

100 S=S+T(J) M(J)

110 NEXT J

120 TO=S/NO

130 PRINT TO

Таблиця 3.3

Програма розрахунку вибіркового значення середнього

квадратичного відхилення

10 REM-OHREDEL SKW

20 DIN T(50), M(50)

25 S = 0

30 PRINT ROL INTERVALOW – N1”

40 INPUT NL

50 PRINT “OBEM VIBORKI NO”

60 INPUT NO

70 PRINT-“SREDNEE –TO”

80 INPUT TO

90 FOR J=1 TO N1

100 PRINT “SREDN I KOL “J” – GO INTERVALA

110 INPUT T(J), N(J)

120 S=S+(T(J)-TO)2 M(J)

130 NEXT J

140 A=SQR (S/NO)

150 PRINT A

160 END

Для розрахунку значень таможна також використати простий метод сум. Для прикладу, що розглядається у випадку клинових пасів наведена розрахункова таблиця для використання метода сум (табл. 3.4).

Таблиця 3.4

Визначення значень та методом сум

Середини часткових інтервалів Тсі,	Частоти mi	Допоміжні коефіцієнти
		К1= 25	К2= 7
75	1	1	1
225	4	5	6
375	14	19	-
525	17	-	-
675	3	4	-
825	1	1	1
	N = 40	Л1= 5	Л2 = 1

В дві перші графи табл. 3.4 переписують значення з 1-го та 2-го рядків табл. 3.1. В третій графі табл. 3.4 роблять прочерк проти найбільшого значення частоти m_i (в нашому прикладі це 17), а в четвертій графі – три прочерку: проти прочерку в тертій графі та зверху і знизу від нього. Далі в третій графі виконують послідовно додавання наростаючим підсумком значень m_i по часткових інтервалах, починаючи від першого значення до прочерку та від останнього значення до прочерку.

Одержані суми складають і підраховують значення двох допоміжних коефіцієнтів К₁ та Л₁. Аналогічно одержують значення допоміжних коефіцієнтів К₂ та Л₂ по четвертій графі. Потім підраховуються допоміжні коефіцієнти М₁ = К₁- Л₁ і М₂ = К₁+ Л₁ + 2К₂+ 2Л₂ потім визначають середнє арифметичне значення напрацювання клинових пасів до першого відказу та вибіркове середнє квадратичне відхилення по рівняннях:

; (3.2)

(3.3)

де Т_{с max} – значення середини часткового інтервалу з максимальною частотою відказів, напроти якого зроблений прочерк в третій графі;

значення напрацювання в границях часткового інтервалу ( в нашому прикладіг).

Результати розрахунків:

г,

Ступінь розсіювання випадкової величини визначається безрозмірною числовою характеристикою – коефіцієнтом варіації:

, (3.4)

де t_зм - величина зміщення зони розсіювання Т₁ відносно нульового значення

Зміщення необхідно приймати чисельно рівним нижній границі першого часткового інтервалу. З таблиць рядів розподілу випадкових величин в наших прикладах у випадку клинових пасів t_зм=0, а у випадку колінчастих валів t_зм=0,5 тис. мото-г. так у випадку клинових пасів коефіцієнт варіації підраховується по рівнянню:

Даний безрозмірний коефіцієнт не тільки використовується як відносна характеристика ступеню розсіювання випадкової величини відносно середнього значення, але і для орієнтованого вибору теоретичного закону розподілу (ТЗР) випадкової величини. Стосовно до завдання, що розглядається, при

  0,33 – закон розподілу вибирається нормальний, а при   0,33 – закон розподілу Вейбулла.

Оскільки в першому прикладі значення   0,33, приймаємо для подальших розрахунків нормальний закон розподілу напрацювання клинових пасів до першого відказу. Цей орієнтований висновок необхідно в подальшому перевірити за допомогою критерію О.М.Колмогорова 1, 2, 3, 4.

3.4. Статистична оцінка ймовірності безвідказного напрацювання та інтенсивності відказівклинових пасів для і-х часткових інтервалів підраховують в наступних рівняннях:

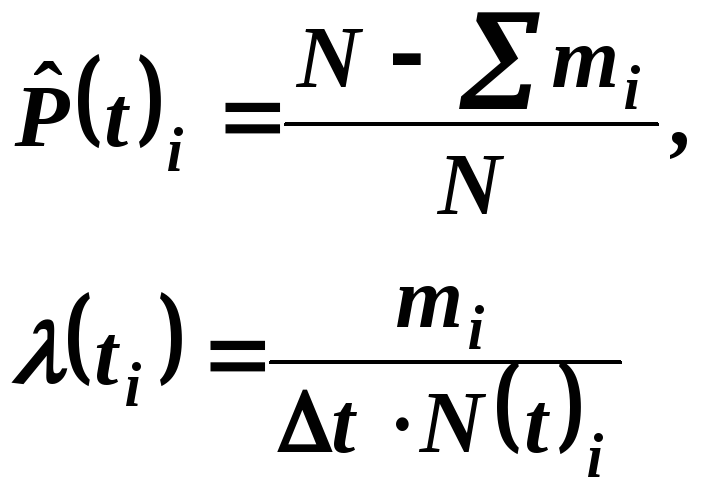, (3.5)

де N – число виробів с початку випробувань (в розглянутому завданні

N = 40);

- значення напрацювання в частковому інтервалі ( у кожному прикладі = 150 г.)

N(t_і) – кількість робото здатних виробів до початку і-го часткового інтервалу

Вихідні дані для підрахунків та їх результати зводять в табл. 3.5

Таблиця 3.5.

Визначення статистичних оцінок та

Показники	Значення показників по часткових інтервалах
	0...150	150...300	300...450	450...600	600...750	750...900
1.Кількість відказів за інтервал, mi	1	4	14	17	3	1
2.Кількість виробів, що відмовили до кінця інтервалу, mi	1	5	19	36	39	40
3. Кількість роботоздатних виробів до початку інтервалу, N(ti)	40	39	35	21	4	1
4.Статистична оцінка,	0,975	0,875	0,525	0,100	0,025	0
5. Статистична оцінка,	0,0002	0,0007	0,0027	0,0054	0,0050	0,0067

3.5. Графік зміни дослідної ймовірності безвідказної роботи будують з використанням відповідних їх значень для часткових інтервалів з табл. 3.5.

Приклад побудови графіка показаний на рис. 3.4.

Між показниками ймовірності безвідказної роботи виробу та інтегральною функцією розподілу напрацювання до першого відказу існує взаємозв’язок, обумовлений рівнянням

_і(3.6)

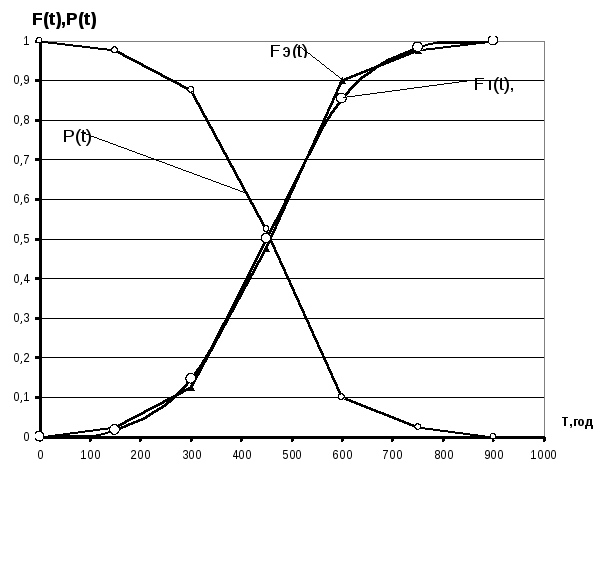
Рис. 3.4. Емпірична та теоретична інтегральна функції розподілу напрацювання клинових пасів до першого відказу та ймовірність безвідказної роботи пасів по даних випробувань на надійність

3.6. Значення теоретичної інтегральної функції F(t) для нормального розподілу з відомими параметрами тавизначаються по табличному інтегралуF(t) =(х) 4,5, який безпосередньо показує ймовірність тої події, що значення випадкової величини знаходяться в границях від 0 до t. Значення функції в кінці і-го часткового інтервалу приймається рівним значенню інтеграла

(х) по додатку 5. Стосовно до завдання, що розглядається

(3.7)

де T_Bi – верхня границя і-го часткового інтервалу значень напрацювання клинових пасів до першого відказу;

г та г.

Наприклад, верхня границя і-го часткового інтервалу Т_Ві=150 г. Тоді , то по додатку 5 значення функції(-2,11)=0,018.

Отже, значення теоретичної інтегральної функції F(t) в кінці і-го часткового інтервалу дорівнює 0,018.

Аналогічно визначають значення F(t) для других інтервалів, записують їх в табл. 3.6. та наносять знайдені значення на рис.3.4., одержуючи графік теоретичної інтегральної функції розподілу F(t).

Таблиця 3.6.