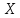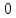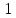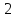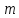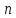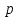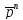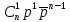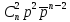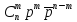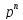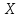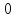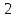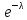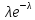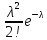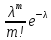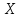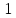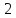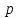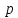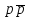Параграф 6. Мода и медиана. Квантили. Моменты случайных величин. Асимметрия и эксцесс

Модой случайной величины называется ее наиболее вероятное значение.

Медианой непрерывной случайной величины называется такое ее значение, для которого:

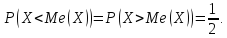
Квантилем уровня называется такое значение случайной величины, при котором функция ее распределения принимает значение, равное:

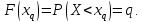
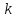Начальным моментом -го порядка случайной величины называется математическое ожидание-й степени этой величины:

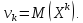
Центральным моментом -го порядка случайной величины 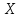называется математическое ожидание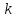-й степени отклонения случайной величины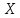от ее математического ожидания:

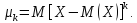
Глава 4. Основные законы распределения Параграф 1. Биномиальный закон распределения

Дискретная случайная величина 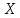имеетбиномиальный закон распределения, если она принимает бесконечное, но счетное множество значений с вероятностями:

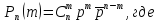
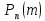–вероятность того, что событие 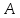наступит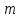раз в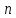независимых испытаниях;

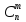–сочетания из 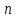элементов по;

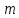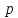–постоянная вероятность наступления события ;

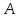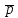–постоянная вероятность того, что событие 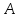не наступит;

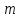–число независимых испытаний, в котором появилось событие ;

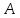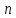–общее число независимых испытаний.

Ряд распределения биномиального закона:

Теорема 1. Математическое ожидание и дисперсия случайной величины 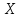, распределенной по биномиальному закону:

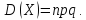
Доказательство.

Теорема доказана.

Пример 1.

Параграф 2. Закон распределения Пуассона

Дискретная случайная величина 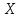имеет закон распределения Пуассона, если она принимает бесконечное, но счетное множество значений с вероятностями:

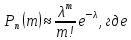
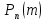–вероятность того, что событие 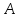наступит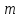раз в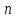независимых испытаниях;

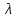–среднее значение числа появления события 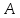при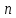независимых испытаниях.

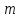–число независимых испытаний, в котором появилось событие ;

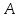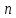–общее число независимых испытаний.

Ряд распределения закона Пуассона:

Теорема 1. Математическое ожидание и дисперсия случайной величины 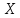, распределенной по закону Пуассона:

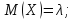
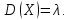
Доказательство.

Теорема доказана.

Пример 1.

Параграф 3. Геометрическое распределение

Дискретная случайная величина 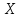имеет геометрическое распределение, если она принимает бесконечное, но счетное множество значений с вероятностями:

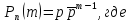
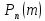–вероятность того, что событие 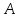наступит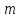раз в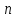независимых испытаниях;

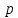–постоянная вероятность наступления события ;

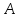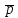–постоянная вероятность того, что событие 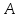не наступит.

Ряд геометрического распределения:

Теорема 1. Математическое ожидание и дисперсия случайной величины 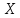, имеющей геометрическое распределение:

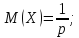
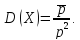
Доказательство.

Теорема доказана.

Пример 1.

Параграф 4. Гипергеометрическое распределение

Параграф 5. Равномерный закон распределения

Параграф 6. Показательный закон распределения

Параграф 7. Нормальный закон распределения

Параграф 8. Логарифмически-нормальное распределение

Параграф 9. 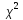распределение

Параграф 10. Распределение Стьюдента

Параграф 11. Распределение Фишера-Снедекора

Глава 5. Многомерные случайные величины

Параграф 1. Понятие многомерной случайной величины

Очень часто результат испытания характеризуется не одной случайной величиной, а некоторой системой случайных величин 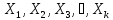, которая называетсямногомерной случайной величиной.

Случайные величины входящие в систему, могут бытьдискретными.

Пример 1. Успеваемость ученика вуза: оценками по различным дисциплинам, проставленным в приложение к диплому.

Случайные величины 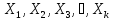входящие в систему, могут бытьнепрерывными.

Пример 2. Погода в данном месте в определенное время суток: температурой, влажностью, давлением, скоростью ветра.

Закон распределения дискретной многомерной случайной величины может быть изображен графически случайной точкой или случайным вектором в n-мерном пространстве.