
- •Раздел 1. Теория вероятности
- •Глава 1. Основные понятия и теоремы теории вероятностей Параграф 1. Понятие о случайном событии
- •Параграф 2. Действия над событиями
- •Параграф 3. Классическое определение вероятности
- •Параграф 4. Статистическое определение вероятности
- •Параграф 5. Геометрическое определение вероятности
- •Параграф 6. Элементы комбинаторики
- •Параграф 7. Теоремы произведения вероятностей
- •Параграф 8. Теоремы сложения вероятностей
- •Параграф 9. Формула полной вероятности
- •Параграф 10. Формула Байеса
- •Глава 2. Повторные независимые испытания Параграф 1. Формула Бернулли
- •Параграф 2. Формула Пуассона
- •Параграф 3. Локальная теорема Муавра-Лапласа
- •Параграф 4. Интегральная торема Муавра-Лапласа
- •Глава 3. Случайные величины Параграф 1. Понятие случайной величины
- •Параграф 2. Действия над случайными величинами
- •Параграф 3. Дискретная случайная величина
- •Параграф 4. Функция распределения
- •Параграф 5. Непрерывная случайная величина
- •Параграф 6. Мода и медиана. Квантили. Моменты случайных величин. Асимметрия и эксцесс
- •Глава 4. Основные законы распределения Параграф 1. Биномиальный закон распределения
- •Параграф 2. Закон распределения Пуассона
- •Параграф 3. Геометрическое распределение
- •Параграф 4. Гипергеометрическое распределение
- •Параграф 2. Дискретная многомерная случайная величина
- •Параграф 3. Функция распределения многомерной случайной величины
Параграф 2. Формула Пуассона
Теорема
1.
Если вероятность
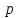 наступления события
наступления события в каждом испытании постоянна и стремится
к нулю при неограниченном увеличении
числа
в каждом испытании постоянна и стремится
к нулю при неограниченном увеличении
числа независимых испытаний, то вероятность
независимых испытаний, то вероятность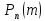 того, что событие
того, что событие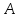 наступит
наступит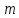 раз в
раз в независимых испытаниях приблеженно
равна:
независимых испытаниях приблеженно
равна:
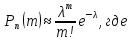
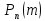 –вероятность
того, что событие
–вероятность
того, что событие
 наступит
наступит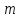 раз в
раз в независимых испытаниях;
независимых испытаниях;
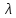 –среднее
значение числа появления события
–среднее
значение числа появления события
 при
при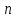 независимых испытаниях.
независимых испытаниях.
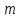 –число
независимых испытаний, в котором
появилось событие
–число
независимых испытаний, в котором
появилось событие
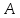 ;
;
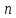 –общее
число независимых испытаний.
–общее
число независимых испытаний.
Доказательство.
Пример 1. Завод отправил на базу 500 доброкачественных изделий. Вероятность того, что в пути изделие повредится равно 0,002. Найти вероятность того, что на базу прибудут 3 поврежденных изделия.
Решение.
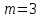 ;
;
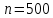 ;
; ;
;
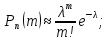
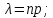

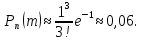
Ответ: 0,06.
Параграф 3. Локальная теорема Муавра-Лапласа
Теорема
1. Если вероятность
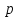 наступления события
наступления события в каждом испытании постоянна и олична
от нуля и единицы при достаточно большом
числе
в каждом испытании постоянна и олична
от нуля и единицы при достаточно большом
числе независимых испытаний, то вероятность
независимых испытаний, то вероятность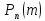 того, что событие
того, что событие наступит
наступит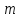 раз в
раз в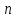 независимых испытаниях приблеженно
равна:
независимых испытаниях приблеженно
равна:


 –вероятность
того, что событие
–вероятность
того, что событие
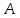 наступит
наступит раз в
раз в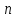 независимых испытаниях;
независимых испытаниях;
 –постоянная
вероятность наступления события
–постоянная
вероятность наступления события
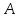 ;
;
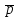 –постоянная
вероятность того, что событие
–постоянная
вероятность того, что событие
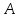 не наступит;
не наступит;
 –число
независимых испытаний, в котором
появилось событие
–число
независимых испытаний, в котором
появилось событие
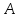 ;
;
 –общее
число независимых испытаний;
–общее
число независимых испытаний;
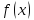 –функция
Гаусса.
–функция
Гаусса.
Доказательство.
Пример 1. Монету бросают 80 раз. Найти вероятность того, что герб появится 20 раз.
Решение.
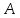 –выпадение
герба;
–выпадение
герба;
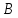 –выпадение
решки.
–выпадение
решки.
События
 и
и образуют полную группу несовместимых
и равновозможных событий.
образуют полную группу несовместимых
и равновозможных событий.

 ;
;
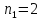 ;
;

 ;
;
 ;
; ;
;
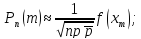
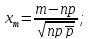


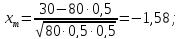
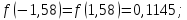

Ответ:
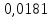 .
.
Параграф 4. Интегральная торема Муавра-Лапласа
Теорема
1. Если вероятность
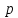 наступления события
наступления события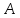 в каждом испытании постоянна и олична
от нуля и единицы при достаточно большом
числе
в каждом испытании постоянна и олична
от нуля и единицы при достаточно большом
числе независимых испытаний, то вероятность
независимых испытаний, то вероятность того, что событие
того, что событие наступит
наступит раз в
раз в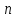 независимых испытаниях заключенное в
пределах от
независимых испытаниях заключенное в
пределах от до
до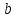 приблеженно равна:
приблеженно равна:


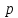 –постоянная
вероятность наступления события
–постоянная
вероятность наступления события
 ;
;
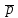 –постоянная
вероятность того, что событие
–постоянная
вероятность того, что событие
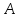 не наступит;
не наступит;
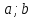 –число
независимых испытаний, в котором
появилось событие
–число
независимых испытаний, в котором
появилось событие
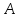 ;
;
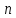 –общее
число независимых испытаний;
–общее
число независимых испытаний;
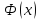 –функция
Лапласа.
–функция
Лапласа.
Доказательство.
Пример 1. При установившемся технологическом режиме завод выпускает в среднем 70 % продукции первого сорта. Найти вероятность того, что из 1000 изделий число первосортных заключается между 600 и 800.
Решение.
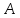 –выпуск
продукции первого сорта.
–выпуск
продукции первого сорта.
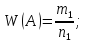
 ;
;
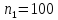 ;
;
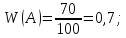
 ;
;
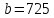 ;
;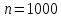 ;
; ;
;

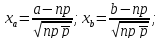
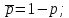



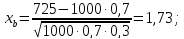
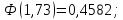

Ответ:
 .
.
Глава 3. Случайные величины Параграф 1. Понятие случайной величины
Случайной величиной называется переменная величина, которая в зависимости от исхода испытания случайно принимает одно значение из множества возможных значений.
Случайные
величины обозначаются большими буквами
латинского алфавита
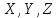 ,
а их возможными значениями соответственно
строчными буквами
,
а их возможными значениями соответственно
строчными буквами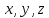 .
.
Случайная величина, принимающая различные значения, называется дискретной случайной величиной, если множество ее значений конечное, или бесконечное, но счетное.
Пример 1. Число родившихся мальчиков среди пяти новорожденных; количество бракованных изделий в данной партии; количество произведенных выстрелов до первого попадания.
Случайная величина, принимающая различные значения, называется непрерывной случайной величиной, если множество ее значений бесконечное и несчетное.
Пример 2. Прирост веса домашнего животного за месяц; дальность полета артиллерийского снаряда; расход электроэнергии на предприятии за месяц.
Законом распределения случайной величины называется всякое соотношение, устанавливающее связь между возможными значениями и соответствующими им вероятности.
