1.3. Деление с остатком.

Помните фильм про Буратино и знаменитый диалог Лисы Алисы и Кота Базилио: “Пять на два не делится! Вот тебе, Базилио, один золотой, а вторую неделящуюся половину я забираю себе!” Кот ничего не понял, но почувствовал, что его обманывают.

Что означает «делится», мы выше видели, это когда есть дополнительный множитель и он восстанавливает равенство. А если множителя нет. Тут мы вступаем на зыбкую почву приближений.

При делении целых чисел и многочленов разные числа и многочлены можно легко сравнивать. У чисел сравнение ведется путем сравнения их модулей, а у многочленов – сравнением их степеней. Поэтому при неполном делении стремятся, что бы степень остатка была меньше, чем степень делителя.

Формально понятие степени можно ввести так.

Определение. Пусть К – кольцо без делителей нуля. Степенью элементов кольца К называется отображение ненулевых элементов кольца во множество натуральных чисел такое, что выполняется условие монотонности:Другими словами, степень произведения не меньше степени сомножителя. (Обратим внимание, что для нуля степень не определена!)

Если определено понятие степени элемента, то можно говорить о делении с остатком.

Определение Кольцо К называется кольцом с алгоритмом деления с остатком или евклидовым, еслиилиr=0.

Евклидовых колец не очень много. Нас же будут в основном интересовать два из них.

Пример 1.

Кольцо целых чисел Z является евклидовым, при этом степенью целого числа является его модуль. Алгоритм деления с остатком в кольце целых чисел изучался в школе.

Пример 2.

Пусть P – поле, тогда кольцо многочленов P[x] является евклидовым, при этом степенью является обычная степень многочлена. Алгоритм деления с остатком – обычное деление многочленов уголком.

Сейчас мы докажем самую полезную теорему о евклидовых кольцах, которая применяется чуть не всей классической алгебре и криптографии.

Но прежде введем понятие наибольшего общего делителя (НОД) и двойственное ему наименьше обще кранное (НОК).

Определение. Элемент d=НОД(a,b) называется наибольшим общим делителем элементов a и b, если выполняются два условия:

1) d\a, d\b – т.е. d - общий делить,

2) Если s\a, s\b , то s\d – наибольший делитель, в том смысле, что он делится на все остальные делители.

Понятие наименьшего общего кратного НОК не так важно как НОД, но его введение поучительно в силу свой двойственности к НОД. «Наибольший» заменяется на «наименьший», «делится» на «делит».

Определение. Элемент m=НОК(a,b) называется наименьшим общим кратным элементов a и b, если выполняются два условия:

1) m: a\m, b\m - общий кратный,

2) Если a\n, b\n , то m\n – наименьшее кратное, в том смысле, что оно делит все остальные кратные.

Фундаментальный факт состоит в том, что в евклидовых кольцах, а значит в кольце целых чисел и кольце многочленов над полем, – НОД существует и его можно выразить через исходные элементы.

Теорема (Основная теорем о евклидовых кольцах).

Пусть К – евклидово кольцо, тогда любые элементы имеют наибольший общий делитель и, более того, такие, чтоd=НОД(a,b)=au +bv.

Доказательство.

а) Применяя свойство деления с остатком получим табличку уменьшающихся остатков. Так как степень каждого остатка – натуральное число, а натуральные числа не могут убывать бесконечно, то табличка будет конечной, а последний остаток нулевым.

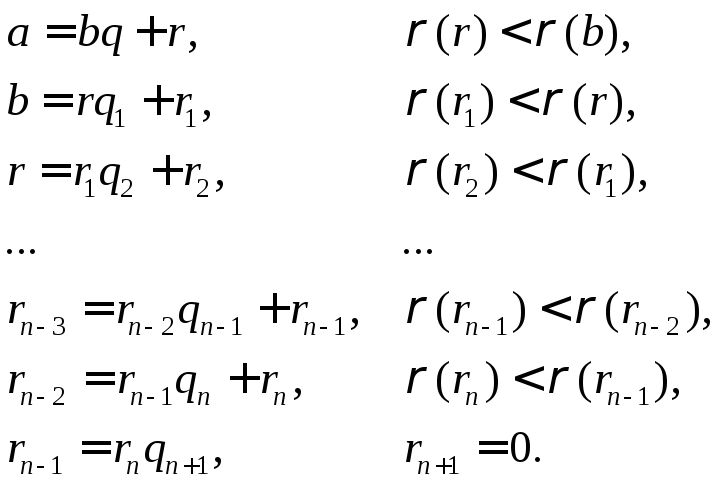
В нашей табличке получилось n+2 строки. Какой же из участвующих в ней элементов является долгожданным НОД? Это последний ненулевой остаток r_n. Для того, чтобы убедиться, что d=r_n, нужно проверить оба свойства НОД. Прежде всего, просматривая табличку снизу вверх, убеждаемся, что r_n делит a и b. В самом деле, последняя строка нам гарантирует, что r_n\r_n-1. Из предпоследней строки следует, что r_n\r_n-2 и т.д. Из третьей строки следует, что r_n\r, из второй, что делит b, а из первой, что r_n\a.

Теперь проверим, что r_n - наибольший делитель, т.е., что он делится на любой s такой, что s\a и s\b. Теперь просматриваем нашу табличку сверху вниз. Из первой строчки следует, что s\r, из второй, что s\r₁ и т.д. Из предпоследней строки следует, что s\r_n. Таким образом, последняя строка даже не понадобилась.

б) Осталось выразить остаток r_n через исходные элементы a и b. Для этого опять просматриваем нашу табличку снизу вверх. Из предпоследней строки получаем r_n =r_n-2+(-q_n)r_n-1, из третьей снизу r_n-1=r_n-3+(-q_n-1)r_n-2, поэтому

r_n=r_n-2+(-q_n)r_n-1=r_n-2+(-q_n)(r_n-3+(-q_n-1)r_n-2)=r_n-2(1+(-q_n)(-q_n-1))+r_n-3(-q_n).

Поднимаясь снизу вверх, мы последовательно выразим r_n через r_n-2 и r_n-1, потом через r_n-3 и r_n-2 и т.д. И, наконец, через a и b.

□

Таким образом, в кольце целых чисел и кольце многочленов над полем всегда можно эффективно найти НОД. Алгоритм, приведенный выше, его называют алгоритмом Евклида, реализован в большинстве компьютерных систем, в том числе и в тех, что используются для нужд криптографии.

Данная теорема имеет массу приложений, например, с ее помощью строятся поля Галуа.

Теорема (Первая теорема о поле Галуа).

Если натуральное число p является простым, то кольцо вычетов Z_p на самом деле является полем.

Эта теорема была доказана в п.5 §3 Главы 1 как утверждение.

Упражнение. Найдите обратные по умножению к остатку 5 в полях Z₇, Z_17, Z₁₂₇. Проще всего обратный искать по алгоритму Евклида.