Свойства символа Якоби:

1. a≡a₁(mod n)

2.

3.

4.

5.

6. 3акон взаимности:

(n,m)=1, n, m>0, n, m — нечетные числа .

Эти свойства нетрудно доказать, воспользовавшись определением символа Якоби и свойствами символа Лежандра.

Очевидно, для символа Якоби выполняются те же свойства, что и для символа Лежандра, за исключением только критерия Эйлера. Критерий Эйлера для символа Якоби не выполняется.

Приведенные свойства символа Якоби позволяют составить алгоритм для вычисления символа Якоби и символа Лежандра:

1. Выделяем из числителя все степени двойки:

2. Пользуясь св-вом 4, понижаем степень k:

3. Если k mod 2=1, то вычисляем 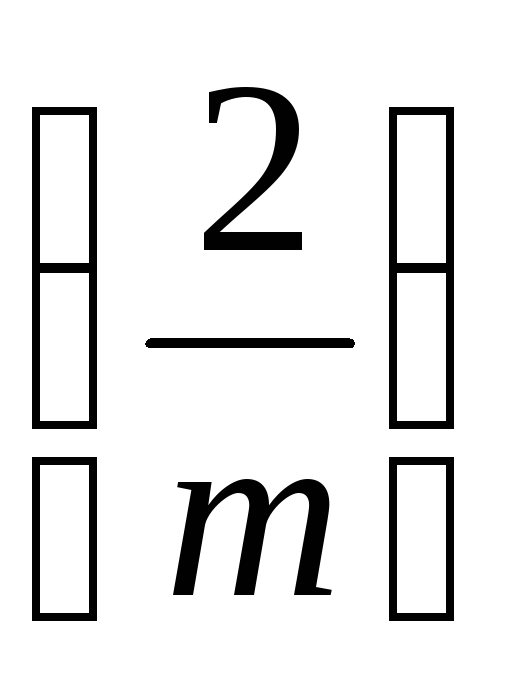пользуясь св-вом 5.

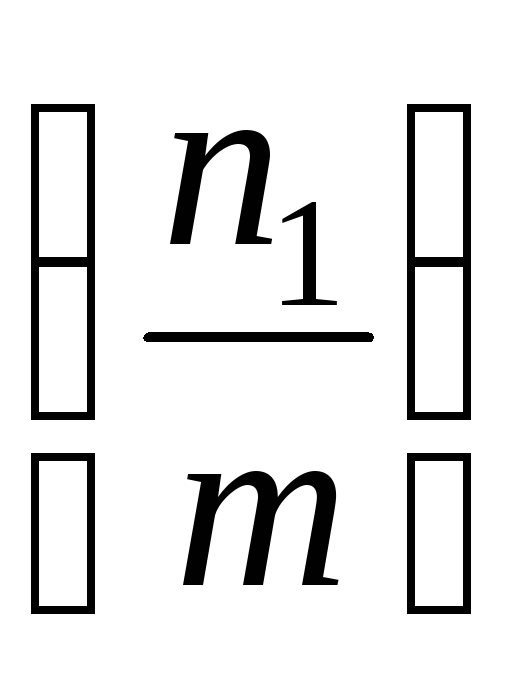4. Символ преобразуем, пользуясь законом взаимности, и затем приводим числительm по модулю знаменателя n₁ и повторяя для получившегося символа Якоби шаги 1-4, пока в числителе не останется 1 или —1.

В более формализованном виде алгоритм выглядит следующим образом:

Алгоритм вычисления символа Якоби:

Вход: n - числитель, m – знаменатель символа Якоби. m – нечетное число,

n, m>0, s=1.

Ш.1: Если (n,m)≠1, то s:=0. Идти на Выход.

Ш.2: n:=n mod m. Ш.3.

Ш.3: Представить n как n=2^kn₁ . k:=k mod 2, n:=n₁.

Ш.4: Если k=1, то если m mod 8 = 3 или m mod 8 = 5, то s:=—s .

Ш.5: Если n=1, то идти на Выход.

Ш.6: Если n=m—1, и m mod 4 = 1, то идти на Выход.

Если n=m—1, и m mod 4 = 3, то s:=—s. Идти на Выход.

Ш.7: n↔m. s:=s·(—1) . Идти на Ш.2.

Выход. s – символ Якоби.

Пример:

.

5.3. Тест на простоту Соловея-Штрассена.

Символ Якоби отличается от символа Лежандра тем, что в первом знаменатель – составное число, а во втором – простое. Алгоритм вычисления символа Якоби и символа Лежандра одинаков, но для символа Якоби не выполняется критерий Эйлера.

Пусть мы имеем нечетное число n, о котором неизвестно, простое оно или составное. Символ является символом Лежандра, еслиn – простое, и тогда для него выполняется критерий Эйлера, то есть .

Если же n – составное число, то символ является символом Якоби, и тогда вышеуказанное сравнение, возможно, не выполняется. (Мы говорим «возможно», так как для некоторыхa и n, в силу случайного совпадения, сравнение может оказаться верным.)

Поэтому если найдется такое a (1 < a < n), что , то можно наверняка утверждать, что числоn – составное. На этом факте основан тест Соловея-Штрассена.

Тест Соловея-Штрассена:

Вход: n – нечетное, t – параметр надежности.

1. Повторять t раз:

1.1 Случайно выбираем a:

1.2. Если “n – составное”. Выход.

1.3. Вычисляем ,

1.4. Если r ≠s “n –составное ”. Выход.

2. “n –простое с вероятностью 1— ε^t ”. Выход.

Как и тест Ферма, этот тест может принять составное число за простое, но не наоборот. Вероятность ошибки (то есть вероятность принять составное число за простое) составляет ε^t, где t – число итераций теста, параметр надежности, а <.

Как видим, оценка надежности теста Соловея–Штрассена гораздо лучше, чем для теста Ферма, даже в том случае, когда φ(n) ненамного меньше n.