5.9. Числа Блюма.

Числа вида n=pq, p, q – различные простые числа, причем p≡3(mod 4), q≡3(mod 4), называются числами Блюма.

Пусть n – число Блюма, и aQ(n). Тогда сравнение x²≡a(mod n) имеет четыре решения, которые можно представить в виде системы: 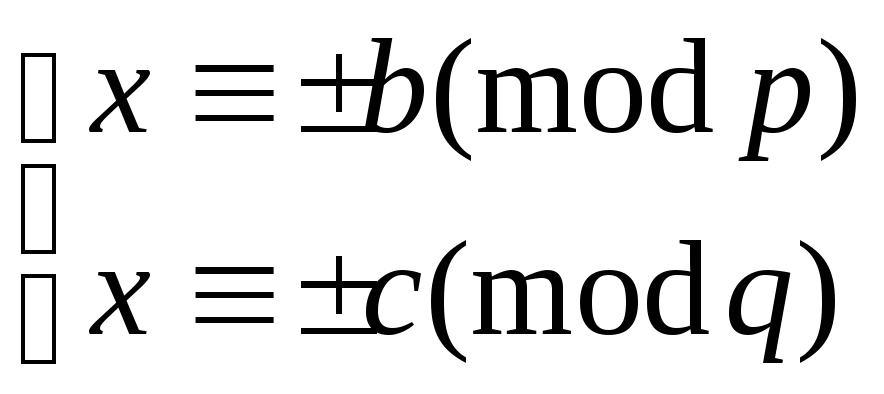. Заметим, что. Аналогично получим. То есть один корень из парыb,—b является, а другой не является квадратом по модулю p, один корень из пары c, —c является, а другой не является квадратом по модулю q.

Таким образом, если n – число Блюма, то один из четырех корней сравнения x²≡a(mod n) является квадратом и один – псевдоквадратом по модулю n. Корень, являющийся квадратом по модулю n, называется главным корнем.

Итак, мы только что показали важное свойство квадратичных сравнений по модулю чисел Блюма: извлекая квадратный корень по модулю Блюма, получаем 4 решения, из одного из которых в свою очередь можно извлечь квадратный корень, и т. д. На этом важном свойстве построено несколько криптосистем.

BBS-генератор (генератор Blum-Blum-Shub):

Параметры генератора: n=pq, p, q – различные простые числа, причем p≡3(mod 4), q≡3(mod 4) (то есть n – число Блюма).

Начальное состояние (ключ генератора): s₀Q(n)

Генерируемая последовательность: BBS(s₀)=z₁, z₂, …, z_m, где z_i=s_i mod 2, i=1,2,…,m, s_i+1=s_i² mod n, i ≥ 0.

Теорема (об условной стойкости BBS-генератора)

Если существует алгоритм, вычисляющий z₀=s₀ mod 2 по BBS(s₀) за полиномиальное время с вероятностью не меньше ½+ε, ε>0, то для любого δ, ½<δ<1, существует вероятностный алгоритм, который различает квадраты и псевдоквадраты по модулю n за полиномиальное время с вероятностью не меньшей δ.

■

Другими словами, если проблема распознавания квадратов и псевдоквадратов по модулю Блюма не решается за полиномиальное время, то BBS-генератор криптографически стоек. Проблему различения квадратов и псевдоквадратов по модулю Блюма действительно считают вычислительно сложной, поскольку в настоящее время она не решается эффективно без факторизации модуля, что служит основанием для признания BBS-генератора стойким.

Криптосистема Блюма-Гольдвассер (Blum-Goldwasser).

Пусть x₁, x₂, … , x_m – последовательность бит открытого текста. В качестве параметров криптосистемы выбираем n=pq – число Блюма, s₀ – случайное число из Z_n, взаимно простое с n.

В качестве открытого ключа для шифрования выступает n, в качестве секретного ключа для расшифрования – пара (p, q).

Для того, чтобы зашифровать открытый текст, обладатель открытого ключа выбирает s₀. На основе BBS-генератора по ключу s₀ получает последовательность квадратов s₁, s₂, … , s_m, по которой получает последовательность младших бит z₁, z₂, …, z_m. Путем гаммирования с этой последовательностью битов открытого текста получает шифрованный текст y_i=x_iz_i, i=1,2,…,m. Шифрограмма, которая пересылается обладателю секретного ключа, есть (y₁,y₂,…,y_m, s_m+1). После формирования шифрограммы последовательность s_i, i=0,1,…,m уничтожается, и при следующем сеансе связи отправитель выбирает новое s₀.

Получатель шифрограммы восстанавливает по s_m+1 последовательность главных корней s_m, … , s₁ и последовательность их младших бит z₁, z₂, …, z_m, а затем расшифровывает шифрограмму: x_i=y_iz_i , i=1,2,…,m.

Криптосистема Гольдвассер-Микали.

Параметры системы: n=pq – число Блюма, z – случайное число из .

Открытый ключ для шифрования – пара (n,z), секретный ключ для расшифрования – пара (p,q).

Пусть x₁, x₂, … , x_m – последовательность бит открытого текста. Бит шифрованного текста вычисляем по биту открытого текста как 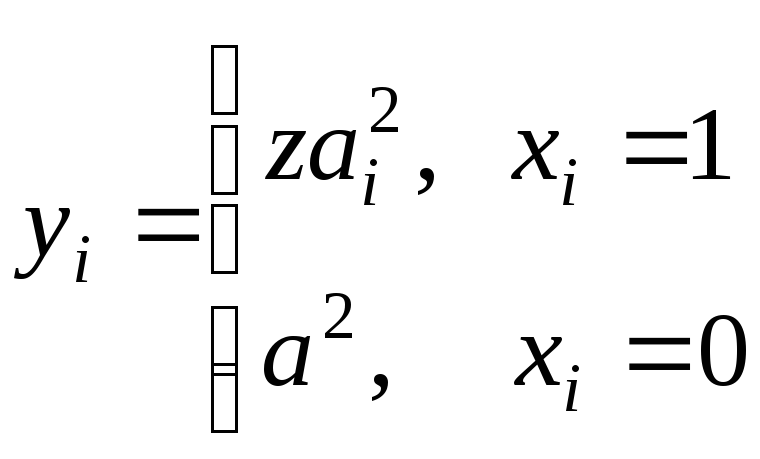, гдеa_i – случайное число из Z_n.

В итоге шифрования получается последовательность не бит, а чисел, причем y_i является псевдоквадратом по модулю n, если x_i =1, и квадратом, если x_i=0.

Адресату, обладающему секретным ключом, отправляется последовательность чисел шифртекста y₁, y₂, …, y_m , после чего параметр z может быть уничтожен.

Адресат осуществляет расшифрование следующим образом:

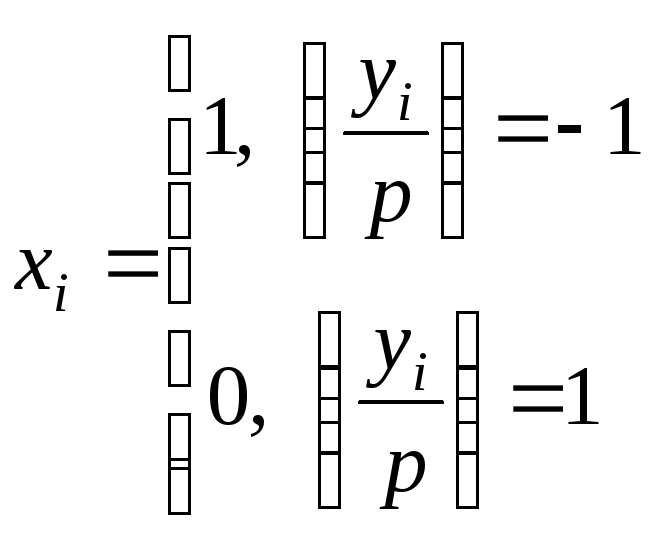, i=1,2,…,m.

Условная стойкость криптосистемы Гольдвассер-Микали основана на предположительной сложности алгоритма распознавания квадратов и псевдоквадратов по модулю Блюма без знания разложения модуля на простые сомножители.

Данная криптосистема имеет существенный недостаток – размер шифртекста значительно превышает размер открытого текста, ведь каждый бит последнего при шифровании преобразуется в число такой же размерности, как n.