Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Национальный исследовательский университет «Высшая школа экономики»

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Линал_Reshebnik.pdf

Скачиваний:

486

Добавлен:

26.03.2016

Размер:

1.51 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 67 / 227 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 > Следующая >>>

59) Найдите собственные векторы и собственные значения оператора дифференцирования в пространстве бесконечно дифференцируемых функций.

Решение

Подробное решение задачи представлено на странице 84 (пример 7.7)

60) Являются ли элементы пространства непрерывных на отрезке [−π,

cos(x) ортогональными относительно скалярного произведения

f , g

Решение

Найдём значение определенного интеграла:

π] функций sin(x) и


		f (x)g(x)dx ?
		f (x)g(x)dx ?

	1		1	cos(x)	1
f (x)g(x)dx sin(x) cos(x)dx		sin(x)dx				(cos( ) cos( )) 0
	2		2		2

Поскольку скалярное произведение (заданное, как определенный интеграл) равно 0, то функции ортогональны (следствие 9.6 теоремы 9.10)

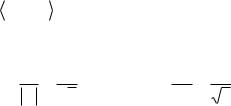
61) Найдите ортонормированный базис, в котором квадратичная форма

2	4x1 x2	4x2	2
Q x1	4x1 x2	4x2		имеет канонический вид.

Решение

Найдем корни характеристического многочлена матрицы квадратичной формы

1		2	0		0
det				1
	2	4			5
				2

Для собственных значений соответствующие собственные векторы:

	0
1
	5
1

4

	2

2		1
		~
4			0
4			0
	2		~
			~

1

2 0

x
1
1

0
0

2x	2
	2
2x	x	2
1		2

	2


	1
	1


	2

Заметим, что векторы Y1 и Y2 ортогональны:		Y1
Таким образом, ортонормированный базис:	P1
(В соответствием с теоремами 8.8 и 11.4)

	Y
		2
	Y
	1
	1
	Y
	1

1 5

1 1
	2


	1

;

	0 Y
		1
	P	Y
	P	2
		2
	2	Y
		Y
		2

	Y
		2
		1
		5
		5

	1

	2
	2

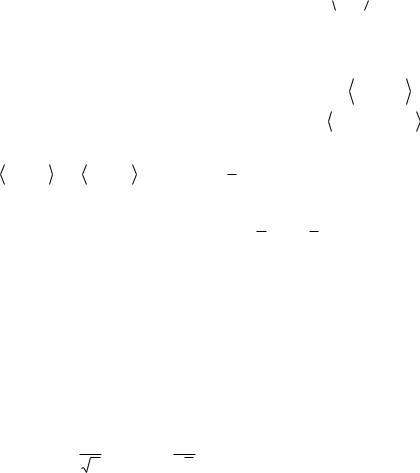
62) Линейное подпространство R3 в некотором ортонормированном базисе задано

уравнением x1 x2	x3	0	. Найдите какой-нибудь ортонормированный базис этого
подпространства.

Решение

При решении номера предполагаем выполнение теоремы 10.5

Имеем уравнение: x1 x2 x3

В векторной форме общее решение уранения может быть записано в виде:

x				1				1
		1
		1
	x	2	C		1	C	2		0
		2	1				2
					0				1
x3					0				1

				Y				Y
					1				2

C	, C		2	R
1			2
C	2	C				2
C		C			2
1					2

, где Y1,Y2 - базис.

Заметим, что базис не является ортогональным: Y1Y2 1 0 (следствие 9.6 теоремы 9.10)

Проведём ортогонализацию базиса. Разложим его на ортогональную составляющую и

ортогональную проекцию: Y Y		Y	, где Y Y	2	. (По теореме 10.4).
1	1	1	1	2

Потребуем выполнения условия ортогональности:
Потребуем выполнения условия ортогональности:	Y1
Подставляя значение ортогональной проекции: Y1	Y2

По свойствам скалярного произведения (теорема 9.10):

Y	0
2

Y
2


Y1	Y2 Y2	Y2	, откуда	1	.
Y1	Y2 Y2	Y2	, откуда	2	.
				2
				1			1		1
						1		1
			Y1 Y2			1		1	2 .
Таким образом, Y1			Y1 Y2	1		2	0	2	2 .
				0		2	1	2	1
				0			1		1

Удалив множитель, получаем ненормированную ортогональную проекцию:

Нормируя базис, то есть сводя его длину к единице, получаем требуемый ортонормированный базис пространства.

Y
Y
1

		1
		2
		2
		1
		1

Ответ: P1

1 1 2 6 1

1 2

	1
	0
	0
	1
	1

В дальнейшем, номера, посвященные теме «ортонормирование базиса» будут сопровождаться лишь короткими комментариями и ссылками на данную задачу для ознакомления с оформлением и перечнем необходимых теорем и определений.


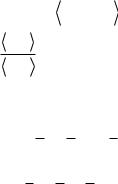
63) Найдите ортогональную проекцию xM	и ортогональную составляющую xM		вектора

x (0, 1, 0) на подпространство М, порожденное вектором		a (10, 20, 10) . Координаты

заданы в ортонормированном базисе.

Решение

Подробный пример решения с необходимыми требованиями к оформлению номера и ссылками на используемые теоремы и определения, приведен к задаче № 62.

Раскладывая вектор на составляющие, имеем:

x x			x
x x		M	x			M
		M				M
Причём			xM				a
Причём			xM				a
													0
Потребуем:							xM				a		0
		x, a					20				1
		a, a					600				30
		a, a					600				30
Тогда:
x				1	,			2	,			1
x	M				,				,
	M			3				3				3
				3				3				3
x			1	,			1	,		1
x	M			,				,
	M		3				3			3
			3				3			3

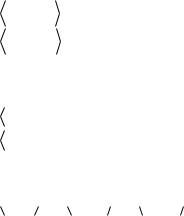
64) Найдите ортогональную проекцию

	x
	x	M
		M

и ортогональную составляющую

	x
	x	M
		M

вектора

x (7, 3, 1)

на подпространство М, порожденное векторами a1

(1, 1, 1)

(4, 0, 5)

Решение

Рекомендуется изучить подробный пример решения похожего номера с необходимыми требованиями к оформлению и ссылками на используемые теоремы и определения, приведенный к задаче № 62.

Потребуем выполнение перпендикулярности вектора x к базисным векторам:

x		, a
x	M	, a
	M	1
xM		, a2

Поскольку

	x a
		1
		x a

		1

a	2

a	2

x x		, а

,a1 0

,a2 0

x

a	2

, имеем:

По свойствам скалярного произведения, имеем:

x, a1 a1 , a1 a2 , a1

x, a2 a1 , a2 a2 , a2

Подставляя соответствующие значения:
3 3 9

23 9 41

В итоге имеем:
2

1
				1	4		2
Таким образом,	x a	a	2	2 1		0	2	.
	1		2
						5	3
				1		5	3

	7	2	5

Откуда, x x x	3	2	1	.
	1	3	4
	1	3	4

65) Пусть x (x1 ,	x2 , x3 ) , y ( y1 , y2 , y3 ) . Может ли функция
F (x, y) x1 y1 2x1 y2		2x2 y1 5x2 y2	2x1 y3 2x3 y1 7x3 y3 служить скалярным
произведением?

Решение

Запишем функцию в матричном виде:

					1	2	2 y
									1
F x	x	2	x	3	2	5	0	y	2
1		2		3					2
					2	0	7	y
					2	0	7	y	3
									3

		1
		2
	Заметим, что матрица	2
		2
		2


	определенной, поскольку

1 2 3

2	2
5	0

0	7

1 0
1 0
13

симметричная, однако она не является положительно

(в соответствии с теоремой 8.6).

Следовательно, это не матрица скалярного произведения. (В соответствии с определением, стр. 139)

66)???Пусть скалярное произведение векторов относительно некоторого базиса задано

формулой

x1 y1 x2 y2

. Найдите формулу для скалярного произведения

относительно нового базиса

e	' (1, 2)
1
e	' (2, 1)
2

Решение

B(x, y) x			x		1	3 y					4x y		4x		y	5x		y
B(x, y) x			x					1	5x y		4x y		4x		y	5x		y
		1		2	3	3				1 1	1	2		2	1		2		2
					3	3	y2
e		(1, 2)
1
e	2	(2, 1)
	2

67) Найдите длину вектора

(1, 1)

относительно скалярного произведения

y	x y		x y	2
	1	1	1	2

x y
2	1

3x2

y	2

							Решение
Запишем скалярное произведение в матричной форме:
B(x, y) x1	x2	1	1 y1		1 1		- матрица скалярного произведения.
B(x, y) x1	x2			, где			- матрица скалярного произведения.

		1	3 y2		1 3
Таким образом, длина вектора					x	x, x 1 1 1 3		6

(в соответствии с определением нормы вектора12 и свойством 4 скалярного произведения согласно теореме 9.10).

12 Страница 140

68) Постройте ортонормированный базис в подпространстве R3, порожденном векторами a1 1, 3, 1 , a2 4, 5, 3 .

Решение

Заметим, что		a1a2	0
Разложение выглядит следующим образом:				a1 a1	a1
Разложение выглядит следующим образом:				a1 a1	a1
	a2
Причём a1	a2
			a2 0
Потребуем:		a1	a2 0
Или a1 a2		a2	0
В соответствии со свойствами скалярного произведения						a1
Откуда:	22
Откуда:	50
	50

411

Получаем: a1 25 5

	1		4		19
		11		1
Наконец, a1	3		5		20
Наконец, a1	3	25	5	25	20
	1	25	3	25	8
	1		3		8

Удаляя сомножитель и нормируя базис, приходим к ответу.

								19				4
Ответ:	P			1					20	, P	1	5	.


	1	19	2	20	2	18	2			2	50
		19		20		18					50

									18			3

a	2	a	2	a	2

69) Является ли самосопряженным оператор с матрицей

1		1	?
произведения
	1	2

Решение

0

	1

1 1

, если матрица скалярного

По теореме 11.1 (и следствию 11.1) оператор самосопряжен тогда и только тогда, когда

выполнено условие:

A A

, где матрица оператора A

, а матрица

скалярного произведения: A

0		1 1		1	1		2
Перемножая эти матрицы, получаем:
	1		1	2		0	1
		1

Заметим, что их перемножение в обратном порядке даёт противоположный результат

1		1 0		1	1

	1	2	1			2
				1

Следовательно, оператор не является самосопряженным

70) Найдите матрицу оператора, переводящего векторы плоскости в их проекции на

прямую с уравнением	x y 0	, относительно базиса из единичных векторов
координатных осей.

Решение

						e		(		1		,	1	)
	e1 (1, 0)					e		(		2		,	2	)
	e1 (1, 0)						1			2			2
							1
Имеем базис:	e2	(0, 1)	и векторы, полученные под действием оператора:								1		1
						(e			) (		1	,	1		)


							2				2		2
											2		2
где : x x	- оператор перевода веторов в их проекции на биссектрису первого
где : x x
координатного угла.
				1		1
					2	2
По теореме 7.1 матрица оператора выглядит следующим образом A					2	2
					1	1
					1	1

Таким образом,		A a a		2		2
Таким образом,		A a a

71) Найдите ядро линейного оператора с матрицей

Решение

Путём элементарных преобразований, приходим к

1		2	3
	4	5	6

	7	8	9

матрице:

1		2
	4	5

	7	8

3
6

9

1
	4
~
	8

2 5 10

3
6
6
12
12

1
	4
~
	0

2	3	1		2
5	6		2	3
		~
0	0		0	0

3
0

0

1
	2
~
	0

0	1
1	0

0	0

Откуда ядро оператора -

x	2	2x
ker :			1
	x		x
		2
			1

(в соответствии с теоремой 7.3)

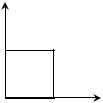
72) Найдите образ единичного квадрата при линейном отображении с формулой

y
	1

y2



x
1
x
	1

2x2

Решение

Единичный квадрат задан точками: A(0,0), B(0,1), C(1,0), D(1,1).

B D

A C

Под действием оператора он переходит в прямоугольник, вершины которого заданы точками: A’(-3,1), B’(-1,2), C’(-2,0), D’(0,1). Данные точки получены поочередной подстановкой изначальных точек в систему уравнений из условия , представляющую линейное отображений.

73) Найдите координаты многочлена

относительно базиса 1,	x, x	2	, x	3	x	2	.

p(x) x	3	3x	2

Решение

относительно базиса

1, x, x	2	, x	3

Запишем базисы и выразим через них многочлен (в нашем примере координаты очевидны, но их также можно было получить с помощью решения матрицы, состоящей из столбцов координат базиса и многочлена).

Отметим, что координаты следует записывать не в виде столбца чисел, а в виде многочлена!

e		1
1
e2		x
e	3	x
	3
e	4	x
	4

2 3

P(x) e	4	3e	e
	4	3	1

h	1
1

h	x
2	x
h	x	2
		2
3	x		x
h	x	3	x	2
		3		2
4

P(x) h	2h	h
4	3	1

74) Найдите координаты

e		'
1
Имеем:
e	2	'
	2

координаты вектора х относительно базиса e1’ , e2’, если известны его {1;4} относительно базиса e1 , e2, причём e1’ =е1+е2, e2’=2е1−е2.

Решение

1


1
	2


	1

Решая расширенную матрицу, состоящую из координат вектора относительно старого базиса и координат перехода от старого базиса к новому, получаем столбец координат вектора относительно нового базиса:

1	2	1	1
			~
	1	4		0
1

Ответ: {3;-1}.

1
~
	0

1 1

1
~
	0

0	3

1
1	1

75) Найдите угол между векторами координатами a 4, 0, 2, 0, 4 и b

с заданными в1, 3, 1, 3, 4

Решение

ортонормированном базисе

В соответствии со следствием 9.7 теоремы 9.10 имеем:

cos( )

a,bab

18 6 6

1 2

угол равен 60º

76) Найдите базис, в котором линейный оператор с матрицей

диагональную форму.

Решение

5

	2

2

8

будет иметь

Найдём собственные значения и собственные векторы линейного оператора как корни характеристического многочлена квадратной матрицы (по теореме 7.7):

	5	2							9
det			0					1
	2	8							4
	2	8						2	4
								2
Собственное значение 1									9		4		2	2		1
Собственное значение 1									9				~

												2	1		0	0
												2	1		0	0

В виде системы 2x1				x2				Соответственно, собственный вектор: Y1									1
В виде системы 2x1				x2				Соответственно, собственный вектор: Y1

																	2
Собственное значение 1									4		1	2	1		2
Собственное значение 1									4				~

											2	4	0		0		2
В виде системы x 2x											2	4	0		0		2
В виде системы x 2x							2		Соответственно, собственный ветор: Y2
			1				2											1
																		1
Таким образом, переходя к базису Y1 и Y2, получаем новую матрицу того же оператора
9	0
	. (По теореме 7.9)

0	4
					2					1
Матрица перехода T											.
						1			2
						1			2

77) Является ли квадратичная форма формой?

Q 25 x	2	14 x x
			2
1		1

Решение

	2x	2
	2x	2
		2

положительно определенной

Для того, чтобы понять является ли квадратичная форма положительно определенной, необходимо определить знак определителей миноров первого и второго порядка этой матрицы. Для этого, прежде всего, запишем матрицу квадратичной формы (на основании теорем 8.2 и 8.5) и вычислим определители ее главных миноров.

25		7	50 49 1
det			50 49 1
	7	2
	7	2

	1	25 0
	1
	2	1 0
	2

да, является

(в соответствии с критерием Сильвестра положительной определенности квадратичной формы, то есть теоремы 8.6).

	1		2	3	, B 7		9 . Найдите	*
78) Пусть	A					8		*	B,
78) Пусть	A					8		AB, A	B,
		4	5	6
		4	5	6

тех случаях, когда умножение определено.

Решение

*	*	,
A	B	,

BA,

B	*	A,

B	*

A	*

AB		, BA

Заметим, что заданные матрицы и матрицы, полученные путём транспонирования исконных, имеют следующие размеры:

A:[2x3] A*:[3x2]

B:[1x3] B*:[3x1]

В соответствии с определением произведения матриц13 умножение определено для следующих пар матриц:

: AB		, BA

Рассчитаем:

	7	8
BA

				7
1		2	3				50
1		2	3		8		50
AB					8

	4	5	6
	4	5	6			132
					9
					9

1		4
			50	132
9	2	5	50	132

	3	6
	3	6

В то же время все остальные комбинации не имеют произведения:

: AB, A B, A B		, BA, B	A, B A
*	* *	*	*	*

13 Страница 48

<<< < Предыдущая 1 2 3 4 5 67 / 227 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
26.03.2016164.86 Кб25Лидерство (Дитс).doc
#
02.06.2015137.73 Кб11Лидерство_программа_2012.doc
#
21.04.2019969.22 Кб7лин.алг..doc
#
26.09.2019709.63 Кб3Линал.doc
#
01.04.20252.83 Mб0линал.docx
#
26.03.20161.51 Mб486Линал_Reshebnik.pdf
#
23.11.20191.89 Mб18Линейная алгебра (лекции, 1 сем,1 курс).docx
#
02.06.2015808.45 Кб24Линейная алгебра.doc
#
26.03.2016629.98 Кб41Линейная алгебра.pdf
#
02.06.20152.64 Mб34Линейное прог. (1).doc
#
02.06.20153.83 Mб8Липяговская Анастасия, презентация.pdf