
- •9)Вычислите .
- •10) Найдите размерность и какой-нибудь базис пространства решений уравнения
- •12) Определите ранг матрицы
- •13) Найдите матрицу X из уравнения
- •14) Является ли система векторов a1=(1,1,1,1), a2=(1,2,3,4), a3=(5,6,7,8), a4=(4,3,2,1), a5=(1,1,-1,-1) линейно зависимой?
- •15) Запишите квадратичную форму, имеющую данную матрицу
- •16) С помощью правила Крамера решите систему уравнений
- •17) Найдите матрицу перехода от базиса e1=(3, 2), e2=(2, 1) к базису e1’=(2, −2), e2’=(−1, 6)
- •20) Найдите размерность и базис линейной оболочки системы столбцов
- •23) Найдите общее решение системы линейных уравнений
- •24) Выясните, являются ли векторы a1=(2, −3, 1), a 2=(3, −1,5), a3=(1, −4, 3) линейно зависимыми.
- •27) Найдите фундаментальную систему решений системы линейных уравнений
- •30) Найдите размерность пространства решений уравнения
- •42) Найдите какие-нибудь матрицы A и В второго порядка, для которых rang (AB)≠rang(BA), или докажите, что таких матриц не существует.
- •43) Является ли линейным пространством множество всех матриц второго порядка (с обычными операциями), у каждого из которых линейно зависимые строки?
- •59) Найдите собственные векторы и собственные значения оператора дифференцирования в пространстве бесконечно дифференцируемых функций.
- •79) Является ли линейным пространством множество всех квадратичных форм с обычными операциями сложения и умножения на вещественные числа?
- •81) Укажите какой-нибудь базис пространства всех симметричных матриц второго порядка.
- •86) Найдите собственные значения и собственные векторы оператора, заданного матрицей
- •91) Запишите в матричном виде квадратичную форму
- •93) Образует ли линейное пространство множество всех невырожденных матриц второго порядка с обычными операциями сложения матриц и умножения матриц на вещественные числа?
- •95) Найдите матрицу линейного функционала, который каждой строке чисел из R3 ставит в соответствие сумму этих чисел.
- •101) Всегда ли произведение симметричных матриц является симметричной матрицей?
- •102) Решите матричное уравнение
- •103) Приведите пример матрицы A размера 3х3, у которой все элементы разные и rang(A)=1, или докажите, что такой матрицы не существует.
- •118) Определите координаты концов A и B отрезка, который точками C(2, 2) и D(1, 5) разделён на три равные части.
- •121) Отрезок с концами в точках А(3, −2) и В(6, 4) разделен на три равные части. Найдите координаты точек деления.
- •122) Даны две смежные вершины параллелограмма А(-2, 6), В(2,8) и точка пересечения его диагоналей М(2, 2). Найдите две другие вершины.
- •123) Разложите вектор v(3,−2) по векторам e1(1, 3), e2(2, −1).
- •124) Даны вершины треугольника: А(1,1), В(4,1), С(4,5). Найдите косинусы углов треугольника.
- •125) Найдите все значения параметра a, при которых точки А(1, а), В(3, 2−а), С(а, −5) лежат на одной прямой.
- •130) Вычислите площадь треугольника ABC с вершинами А(1,1,1), В(2,3,4), С(4,3,2).
- •131) Вычислите объём тетраэдра с вершинами А(1,1,1), В(2,0,2), С(2,2,2), D(3,4,−3).
- •135) При каком значении параметра a точки А(1, 2, 3), В(2, -1,5) и С(-1, а, -1) расположены на одной прямой?
- •По следствию 9.10 теоремы 9.19 эти плоскости не являются параллельными. Следовательно, они пересекаются не под прямым углом, поскольку также 1*1+2*0+3*3 отлично от нуля.
- •144) Нарисуйте параллелепипед и укажите те его диагонали, которые соответствуют векторам a+b-c и a-b+c, если векторы a, b, c соответствуют ребрам этого параллелепипеда.
- •145) Нарисуйте параллелепипед и укажите те его диагонали, которые соответствуют векторам a+b-c и a-b+c, если векторы a, b, c соответствуют ребрам этого параллелепипеда.
- •152) Начало координат перенесено в точку (2, 1), а оси координат повернуты на угол 60 градусов. Как в такой системе координат будут записываться координаты прежнего начала координат?
- •165) Найдите какой-нибудь базис в пространстве всех векторов их R3, перпендикулярных вектору {1,2,3}.
- •166) При параллельном переносе точка А(1, 2, 3) переходит в точку А’(3,1,2). В какую точку переходит точка В(2, 3, 1)?
- •189) Укажите какой-нибудь базис в пространства всех квадратичных матриц на R2 (с обычными операциями).
- •194) Образует ли линейное пространство множество всех ступенчатых матриц третьего порядка с обычными операциями?
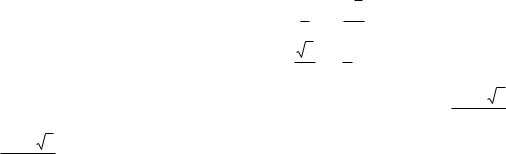
152) Начало координат перенесено в точку (2, 1), а оси координат повернуты на угол 60 градусов. Как в такой системе координат будут записываться координаты прежнего начала координат?
Решение
Для решения задачи воспользуемся теоремой 9.18, согласно которой уравнение связи
координат выглядит следующим образом:
x |
cos |
|
|
|
|
|
|
|
y |
sin |
|
sin x' |
x |
||
|
|
|
|
cos |
|
|
|
y' |
y |
||
0 0
. Или в нашем
случае:
|
|
|
|
|
|
|
|
|
|
1 |
|
x |
cos(60) |
sin(60) x' |
|
2 |
|
|
|||||
|
2 |
||||||||||
|
|
|
|
|
|
|
|
|
|||
|
|
|
cos(60) |
|
|
|
1 |
|
|
3 |
|
y |
sin(60) |
y' |
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
||

 3 2
3 2
1 2
x' y'
|
2 |
|
|
|
|
|
1 |
|
|
|
|
. Таким образом, в
новой системе координат новые будут записываться по формуле: |
x |
x' y' |
3 |
2 |
, |
||||
2 |
|
||||||||
|
|
|
|
|
|
|
|
|
|
y |
x' y' |
3 |
1 |
. В частности для начала координат новые координаты будут записываться |
|||||
2 |
|
||||||||
|
|
|
|
|
|
|
|
|
|
как (2, 1), что, на самом деле, указано в условии.
165

153) Запишите уравнение прямой, проходящей через точки А(−3, 1) и В(1, 2), в виде
Ax By C 0 .
|
|
|
|
Решение |
|
|
|
|
|
|
3A B C 0 |
, просто подставив в данное уравнение прямой |
|
||||||||
Запишем систему: |
|
|
|
|||||||
A 2B C 0 |
|
|
|
|
|
|
|
|
||
|
B |
4 |
|
|
|
|
|
|||
|
A |
|
B |
|
C |
|
||||
|
. Поэтому уравнение прямой x |
y |
|
|||||||
значения точек. Откуда находим: |
|
|
||||||||
C |
A |
A |
||||||||
|
|
7 |
|
|
|
|||||
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
||
|
A |
|
|
|
|
|
|
|||
проходящее через точки А и В выглядит следующим образом: |
x 4 y 7 0 . |
|
|
|
||||||
0
,
166

154) Найдите квадратичную функцию, график которой проходит через точки |
A1 ( 2, 12) |
A2 (0, 2) , A3 (1, 0) . |
|
Решение
Известно, что в общем виде уравнение квадратичной функции выглядит так:
Ax |
2 |
Bx C y . Таким образом, подставив значения трех точек в это уравнение, |
|
,
4 |
2 |
1 |
12 |
|
|
|
|
0 |
0 |
1 |
2 |
|
|
составим систему: |
|
. С помощью элементарных преобразований, приведем |
||||
|
1 |
1 |
1 |
0 |
|
|
|
|
|
||||
1 |
1 |
1 |
0 |
|
|
ее к ступенчатому виду и найдём решение: |
0 |
6 |
3 |
12 |
. |
|
0 |
0 |
1 |
2 |
|
|
|
||||
Таким образом, квадратичная функция, график которой проходит через данные три точки:
y x |
2 |
3x 2 . |
|
|
167

155) Запишите в виде
A1 (2, 1, 3) |
, |
A2 ( 1, 2, 5) |
Ax By
, A3 (3, 0,
Cz D 1) .
0 |
уравнение плоскости, проходящей через точки |
Решение
Подставив, данные точки в уравнение плоскости, получим систему уравнений и найдём ее
решение из матрицы:
|
2 |
1 |
3 |
|
1 |
2 |
5 |
|
|||
|
3 |
0 |
1 |
|
1
1
1
. Заметим , что неизвестных в уравнении плоскости
четыре, в то время как точек, а, следовательно, и уравнений в системе, лишь три, поэтому для того, чтобы найти параметры, мы переписали выражение плоскости в виде
A |
x |
B |
y |
C |
z 1 |
0 |
|
D |
D |
D |
|||||
|
|
|
|
уравнения плоскости -
2 y z 1 0 .
и нашли три неизвестные дроби из этого уравнения. Параметры
A 0 |
|
B 2D |
, а, значит, само уравнение можно записать как |
C D |
|
168

156) Запишите
A(1, 2) |
, B(2, 1) |
уравнение и найдите центр окружности, проходящей через точки
, C(0, 1) .
Решение
Расстояние от любой точки окружности до центра одинаково и, как известно, равно
(x1 x2 ) |
2 |
( y1 y2 ) |
2 |
. Пусть центр окружности − точка О с координатами (x, y). Таким |
|||||||||
|
|
||||||||||||
|
|
|
|
|
(x 1) |
2 |
( y 2) |
2 |
|
(x 2) |
2 |
( y 1) |
2 |
|
|
|
|
|
|
|
|
|
|||||
образом, можем записать систему: |
|
|
|
|
|
|
|
|
, где мы |
||||
|
|
|
|
|
(x 1)2 |
( y 2)2 |
|
(x 0)2 |
( y 1)2 |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
обозначили, что расстояние от центра до точки А равно расстоянию от центра до точки В (первая строка), а также расстоянию от центра до точки С (вторая строка).
(x 1)2 |
( y 2)2 |
(x 2)2 |
( y 1)2 |
|
|||
|
|
|
|
|
|
|
|
|
1)2 |
( y 2)2 |
(x 0)2 |
( y 1)2 |
|
||
(x |
|
||||||
|
|
|
|
|
|
|
|
x 2 |
2x 1 y 2 |
4 y 4 x 2 |
4x 4 y 2 |
2 y 1 |
|||
|
|
|
|
|
|
|
|
|
2x 1 y 2 |
4 y 4 x 2 |
y 2 2 y 1 |
|
|||
x 2 |
|
||||||
|
|
|
|
|
|
|
|
x 3y |
|
|
|
|
|
|
|
|
|
y |
|
|
|
|
|
x 2 |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
x 1,5 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y 0,5 |
|
|
|
|
|
|
|
169

157) Напишите уравнение прямой, проходящей через точку А перпендикулярно вектору
BC , где A(1, 2) |
, B(1, 2) |
, C( 1, 1) . |
Решение
Найдём координаты вектора ВС22:
BC ( 2,
1)
. Вектор, перпендикулярный ему - (-1, 2), в
соответствии со следствием 9.6 теоремы 9.10 (то есть их скалярное произведение равно нулю). Таким образом, по теореме 9.16, в параметрическом виде уравнение прямой, проходящей через точку А, параллельно вектору (-1, 2), то есть перпендикулярно вектору
ВС , записывается как
y 2x 0 .
|
x 1 t |
|
|
y 2 2t |
|
. Его можно также привести к обычному виду:
22 Страница 111
170
158) Найдите какие-нибудь два ненулевых перпендикулярных между собой вектора среди всех векторов, параллельных плоскости 2x 2 y z 3 0 .
Решение
По теореме 9.19, нормалью к данной плоскости служит вектор n{2; -2; 1}. Перпендикулярным ему (т.е. параллельным плоскости) является множество векторов
{a; b; c}, таких что |
|
2a 2b c 0 |
по следствию 9.6. Найдём такие два вектора {a1; b1; c1} |
||||||||||||||
и |
|
{a2; |
|
b2; |
c2}, |
что a1a2+b1b2+c1c2=0. То |
есть можно составить |
систему: |
|||||||||
a |
a |
2 |
b |
b |
2 |
c |
c |
2 |
0 |
|
|
|
|||||
|
1 |
|
|
|
1 |
|
|
1 |
|
|
|
|
|
|
|||
|
2a1 |
2b1 |
|
c 0 |
. Заметим, |
что эта система |
содержит 6 неизвестных и |
лишь 3 |
|||||||||
|
|
|
|||||||||||||||
|
|
2a |
|
2b |
|
c 0 |
|
|
|
|
|||||||
|
|
2 |
|
|
|
|
|
||||||||||
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
||
уравнения, то есть имеет бесконечное множество решений. Таким образом, в качестве ответа к задаче можем привести любую пару векторов, удовлетворяющих системе.
Например: (2; 1; -2) и (1; 2; 2).
171
159) Найдите уравнение какой-нибудь прямой, содержащейся в плоскости с уравнением
x
y 2z 6
0
.
Решение
Поскольку через любые две точки можно провести прямую и причём только одну, наша задача сводится к тому, чтобы взять любые две точки плоскости и провести через них прямую. При этом прямая будет лежать в плоскости, потому что состоит из точек, ей принадлежащих.
Например, возьмём точки (1; 1; 3) и (2; 0; 2). Уравнение прямой, проходящих через эти
две точки в параметрическом виде (по теореме 9.21) выглядит так:
x 1 t
y 1 t
z 3 t
.
Обратим внимание на то. Что при t=0 мы получаем координаты первой точки, при t=1 - координаты второй. Подставляя любое другое значение t, vs получим координаты точки, которое обращает в равенство уравнение плоскости. Более того, если подставить равенства из параметрического уравнения прямой в уравнение плоскости, оно будет верным!
172

160) Найдите угол между вектором a (1, 2, 3) |
и векторным произведением |
b (4, 5 6) . |
|
Решение
Найдём векторное произведение векторов23:
[a,b]
, где
i |
j |
k |
[a, b] 1 |
2 |
3 |
4 |
5 |
6 |
12i 5k 12 j 8k 15i 6 j
6 j
3i 3k
.
По следствию 9.7 теоремы 9.10 угол между вектором а и векторным произведением равен:
a,[a, b] |
|
1* ( 3) 2 * 6 3 * ( 3) |
0 |
||
a [a, b] |
1 4 9 |
9 9 36 |
|||
|
|
||||
23 Страница 119
173

161) Проверьте свойство смешанного произведения
a (1, 2, 3) |
b (3, 1, 2) c (2, 3, 1) . |
Решение
(a,b,c) |
[a,b],с |
для векторов
Найдём векторное произведение векторов24:
i |
j |
k |
[a, b] 1 |
2 |
3 |
3 |
1 |
2 |
4i k 9 j 6k 3i 2 j
i 7 j 5k
.
Скалярное произведение вектора
равно [a,b],c 1* 2 7 *3 5*
с
1
и
векторного произведения двух других векторов
18 .
Смешанное произведение трех векторов равно
Что и требовалось доказать.
1 |
2 |
[a, b] 3 |
1 |
2 |
3 |
3 2 1
1 27 8 6 6 6
18
.
24 Страница 119
174

162) Вычислите
 [a,b],b
[a,b],b
для векторов
a
(1, 2, 3)
Решение
,
b
(3, 1,
2)
.
Найдём векторное произведение данных векторов по определению векторного
произведения:
i |
j |
k |
[a, b] 1 |
2 |
3 |
3 |
1 |
2 |
4i k 9 j 6k 3i 2 j
i 7 j 5k
.
Тогда скалярное произведение
1*3 7 *1 5* 2 3 7 10 0
перпендикулярно.
это вектора и вектора b по теореме 9.10 равно
. То есть векторное произведение векторов им
175

163) Симметричны ли точки
x 1 |
|
y 2 |
|
z 1 |
? |
|
2 |
1 |
1 |
||||
|
|
|
A(1, 2, 1)
и
B(5,
4, 1)
относительно прямой
Решение
176
164) Укажите какой-нибудь вектор, параллельный плоскости
Решение
x 2 y 3z 4
0
.
Нормаль к плоскости по теореме 9.19 - вектор, ей перпендикулярный - это вектор с координатами (1; 2; 3). По следствию 9.6 скалярное произведение этой нормали с любым перпендикулярным ему вектором равно нулю. Иными словами, множество перпендикулярных векторов задано уравнением a 2b 3c 0 . Например, это вектор (3; -1; -1). Он будет параллелен данной плоскости.
177
