Uchebnik3_3

Структура теста.

В данном разделе Вы можете пройти блиц-тест на пройденные темы. Ответ на каждый вопрос должен занимать у Вас не более 2 0 секунд. Все задания теста

Блиц-тест. являются авторскими, цель теста - проверить,

насколько осмыслен пройденный материал. Все задания простые и подразумевают устное решение.

Обратите внимание: тест не является непосредственной подготовкой к экзамену, он может быть полезен лишь как инструмент для поиска пропущенный знаний.

Интерактивная версия доступна под управлением операционных систем Apple в программе iBooks. Если Вы используете бумажную или P D F-версию, Вы можете сверить ответы по материалам в блоке

«Дополнительное» в конце пособия.

Желаю удачи!

80

Тест.

Векторы и матрицы

Вопрос 1 из 8

Если вектор m является собственным для некоторой матрицы А, является ли собственным вектор −m?

A.Да

B.Нет

C.Не во всех случаях

Проверить ответ

Пределы

Вопрос 1 из 5

Вычислите устно:

1

A. 5

B. +∞

C. −∞

D. 1

Проверить ответ

81

Неопределенный интеграл.

Еще со школы мы знаем, что интегрирование - это операция, противоположная дифференцированию.

Поэтому интегрирование используется практически во

Интегралы. всех случаях, когда используется и дифференцирование (в процессе решения

практических задач), а в упрощенных примерах эти операции совмещаются в том числе в дифференциальных уравнениях, о которых речь еще пойдет позже.

Прежде всего необходимо уметь брать простейшие интегралы. Чтобы взять интеграл, нужно задать себе вопрос: «Что нужно продифференцировать,

чтобы получить имеющуюся подынтегральную

функцию?» Под «подынтегральной функцией»

понимается то выражение, которое заключено между знаком интеграла и знаком дифференциала ( dx - знак

дифференциала. Он показывает, по какой переменной

82

мы интегрируем). Например, в интеграле ∫ 2xdx подынтегральной функцией будет

2x . Поэтому, чтобы взять интеграл, надо задаться вопросом, чем было 2x « в

прошлой жизни», до того, как от этого искомого выражения взяли производную и получили 2x?

значение производной показывает нам скорость роста функции в точке.

Ниже приведены примеры для нашего случая: для каждой из этих функций производной будет 2x, то есть при каждом конкретном значении х функции растут одинаково быстро (просто на разной «высоте»).

83

Легко понять: чтобы уметь находить выражения, от которых нужно взять производную, чтобы получить имеющуюся функцию, надо уметь дифференцировать. Фактически, это очень близкие вещи: чем лучше Вы дифференцируете, тем лучше интегрируете, и наоборот. Почти. Дело в том, что для дифференцирования существуют довольно простые правила, некоторые из которых мы уже рассмотрели. Но в случае со взятием интеграла не все так просто:

есть лишь некоторые табличные значения и множество различных «стандартных» способов. Однако каждый раз можно столкнуться с неопределенностью в той или иной степени: выбор способа для взятия интеграла - всегда за Вами, а иногда при решении нужно придумать и что-то свое. Ниже речь пойдет, в основном, о «стандартных» способах, хотя при желании можно найти и несколько оригинальные задачи.

Табличные интегралы.

Для взятия множества простейших интегралов достаточно вызубрить и запомнить (а лучше - просто понять) несколько правил. Например:

Конечно, это лишь несколько примеров тех табличных равенств, которые стоит помнить наизусть. Подробные таблицы можно найти в Интернете. При этом любую из наших формул легко проверить: достаточно помнить, что стоит от ответа взять производную, и мы должны получить подынтегральную функцию (по определению интеграла).

Метод замены переменной.

заменяют то, что мешает вычислению ответа по таблицам (мешает сведению к

84

простейшему случаю). Вероятно, правильный выбор замены приходит с опытом интегрирования.

В данном случае стоит заменить подкоренное выражение:

подставить теперь вместо него в интеграл u, получим: ∫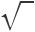

такой интеграл дальше уже невозможно, ведь мы договаривались, что дифференциал показывает, по какой переменной мы интегрируем. Поэтому, раз у

приращения функции. В нашем одномерном случае (единственная переменная - х) дифференциалом будет производная, умноженная на приращение аргумента.

Таким образом, du = 2dx ( 2 - производная функции u(x) = 2x + 5, а dx - приращение аргумента). Конечно, из равенства du = 2dx мы имеем право выразить dx через du:

1

dx = 2 du. Осталось подставить это в наш интеграл:

В ходе решения мы продемонстрировали еще одно важное свойство

1

интегрирования: мы вынесли 2 из-под знака интеграла для упрощения дальнейших вычислений. В самом деле, любой число (если оно - множитель,

конечно) можно вынести из-под знака интеграла, это легко понять, задумавшись о природе интеграла («что нужно продифференцировать, чтобы...?» Вспомним, что дифференцирование «сохраняет» числовые множители). На предпоследнем же

85

Наш ответ почти готов, осталось только вместо u подставить выражение с иксом,

ведь задача изначально не включала в себя никаких u:

В чуть более сложных случаях за новую переменную удобно брать то

выражение, производная которого уже содержится в интеграле как

множитель. Рассмотрим пример:

(C) 6.29. Найти неопределенный интеграл: ∫ sin(lnx) dxx .

Тут хорошо ввести замену u = lnx, так как производная от lnx уже содержится под

∫ sin(lnx) dxx = ∫ sinudu = − cosu + C = − cos(lnx) + C.

86

Метод интегрирования по частям.

Фактически, речь идет о двойной замене. Формула для этого метода выглядит так:

∫ udv = uv − ∫ vdu.

Конечно, метод имеет смысл применить, если найти ∫ vdu проще, чем изначальный

∫ udv. Метод интегрирования по частям очень удобно использовать тогда, когда в

Для примера, найдем (А) ∫ (x + 2)sin2xdx. В качестве линейного множителя ax + b

здесь выступает выражение x + 2. В самом деле, без него мы бы сразу дали ответ (по

приведенной выше. Таким образом, что-то из выражения (x + 2)sin2xdx - это u, а

остальное - dv.

Итак, мы договорились что линейный множитель - это u. Тогда остальное - dv:

87

аргумента» . То есть, sin2x - это производная функции v(x), которую мы и хотим

найти. Как найти функцию, если нам известна ее производная? Проинтегрировать.

Таким образом, v(x) = ∫ sin2xdx . Этот интеграл мы уже находили на предыдущей

прибавляем С к нашему ответу: этот шаг возможен ради упрощения дальнейших вычислений (почему в данном случае мы имеет право так сделать - см. во вкладке для интересующихся читателей).

На равенство dv = sin2xdx в смысле нахождения зависимости v(x) можно взглянуть немного с другой стороны: почему бы просто не проинтегрировать обе стороны равенства?

лучше сказать - семейство функций, таким образом, в начале темы семейством являлось множество функций x2 + C, а частными представителями этого семейства - x2 , x2 + 2 и x2 − 1, графики которых изображены на странице 8 3), производная

рассматривать v как переменную (вместо привычного х).Таким образом, мы опять

88

d(x + 2) = (x + 2)′dx! = dx.

Теперь нужно проделать уже известные операции:

∫ vdu = ∫ − cos22 x d(x + 2) = ∫ − cos22 x dx = − 12 ∫ cos2xdx = − 12(sin22 x )+ C = − sin24 x + C

Теперь все готово для записи ответа:

∫ (x + 2)sin2xdx = (x + 2) (− cos22 x )− (− sin24 x + C).

Заметим, что при раскрытии скобок С свой знак не поменяло. В самом деле, по смыслу вместо С мы можем подставить любую константу: тогда какая разница, с

каким знаком записывать С? Для красоты лучше писать с плюсом.

Определенный интеграл.

Для того чтобы вычислить определенный интеграл, необходимо сначала вычислить соответствующий ему неопределенный интеграл. Например:

мы нашли ответ на аналогичную задачу для неопределенного интеграла, справа от ответа дописываем вертикальную черту с теми же самыми значениями 1 и 3 (эти

числа - верхний и нижний пределы интегрирования соответственно): это

89