Uchebnik3_3

____________________________

Для интересующегося читателя:

Бывает нужно показать, откуда берутся формулы дифференцирования (например,

для Ваших коллоквиумов). Оказывается, удобно пользоваться фактом

(ef(x))′!= ef(x) f ′(!x). Пример: (ax)′!= (exlna)′!= exlna lna = axlna . Однако для более сложных формул следует использовать понятие обратной функции.

Рассмотрим пример y = lnx. Очевидно, y = lnx x = ey. Отсюда становится ясным,

что (lnx)′!= (e1y)′y!= e1y = 1x . Если эти переходы не являются очевидными, стоит

порефлексировать над графиком y = lnx , оценивая значение производной и соизмеряя с соответствующим значением для x = ey.

Часто бывает полезно знать производные гиперболических функций:

(shx)′!= chx, (chx)′!= shx, (thx)′!= ch12x , (chx)′!= − sh12x и другие.

____________________________

Кроме этого, вспомним принцип дифференцирования сложной функции на примере:

(А) Найдите (ecos35x)′!. При нахождении производной мы должны переходить от внешнего уровня к внутреннему. На внешнем уровне мы видим (ef(x))′,!не задаваясь вопросом, что конкретно фигурирует в роли f (x). Согласно правилу, мы должны взять производную от «внешнего уровня» , и умножить на производную того, что

«внутри» то есть на производную f (x). Сделаем это:

(ecos35x)′!= ecos35x (cos35x)′.!

60

Будем продолжать «раскрывать» нашу сложную функцию таким образом дальше:

(ecos35x)′!= ecos35x (cos35x)′!= ecos35x 3cos25x (−sin5x) 5.

Нахождение уравнения касательной.

Касательная к графику функции на плоскости - это прямая, значит, она может быть записана в виде y = kx + b (или же x = a, если прямая вертикальна). Пока что сосредоточимся на случае y = kx + b. Найти уравнение касательной - значит найти

конкретные значения k и b. Со школы мы помним, что для касательной к графику функции f (x) в точке x0:

k = f ′(!x0)

Коэффициент b может быть найден подстановкой конкретного значения k в

уравнение y = kx + b. Рассмотрим пример:

координатами ( − 3;5). При x = − 3 прямая касается графика функции f (x), значит,

искомая касательная тоже проходит через T( − 3;5). Поэтому мы можем подставить

эти координаты в уравнение касательной (и у нас выйдет верное равенство).

Иногда функция может быть задана неявно . Это означает, что у нас не будет записи вида у= . . . где справа содержится какое-то выражение, зависимое исключительно от х. Вместо этого в условии будет дано уравнение, где x и y

следуют вперемешку. Например: xy = ex+5y − 6 . При этом выразить у через х не

61

всегда представляется возможным. Например, для функции, заданной уравнением xy = ex+5y − 6 попытка выразить у через х займет у Вас очень много времени, а толку от этого будет мало. Тем не менее, в задании может требоваться найти,

например, касательную к графику такой функции.

Попытаемся решить эту задачу для нашей функции, заданной равенством xy = ex+5y − 6.

(А) Запишите уравнение касательной, проведенной к графику функции y = y(x), заданной уравнением xy = ex+5y − 6 в точке M( − 5;1) .

производные этих выражений будут равны. Таким образом, мы имеем полное право продифференцировать обе части нашего уравнения.

Для начала возьмем левую часть: чему равна производная xy? Вспомним, что у - это не параметр, а некоторая функция от х. Все дело в том, что задана она в неявном виде, и мы решили не пытаться выразить у через х. Тем не менее, у можно выразить через х (и WolframAlpha отлично с этим справляется), поэтому вместо у можно представлять себе какое-то очень сложное выражение от х. То есть, xy - это

хотелось бы вместо y′!написать что-то более конкретное, но это невозможно, ведь у нас нет формулы для у. Поэтому оставим все как есть:

(xy)′!= y + y′x!.

Рассмотрим правую часть исходного равенства: ex+5y − 6. Возьмем производную от этого выражения:(ex+5y − 6)′!= ex+5y (x + 5y)′.!Тут мы ничего сложного не сделали,

просто следовали инструкциям со страницы 56: мы видим (ef(x))′,!и раскрываем эту производную стандартным образом. Продолжим процесс:

(ex+5y − 6)′!= ex+5y (x + 5y)′!= ex+5y (1 + 5y′)!.

62

Все просто: на последнем шаге мы взяли производную от скобки, то есть, от каждого слагаемого в отдельности.

Итак, получилось:

xy = ex+5y − 6.

(xy)′!= y + y′x!, при этом (ex+5y − 6)′!= ex+5y (1 + 5y′)!.

Поэтому y + y′x!= ex+5y (1 + 5y′)!.

Тут мы использовали наше рассуждение о том, что раз выражения слева и справа от знака «равно» равны, то и их производные должны быть равны.

Зачем был проделан этот путь? Вспомним, что у нас была точка на графике функции, заданной неявно. А именно, точка M( − 5;1). Раз точка М лежит на графике, то мы можем «подставить» ее в наше уравнение xy = ex+5y − 6 и получить

верное равенство. Так, легко убедиться, что М на самом деле лежит на графике y = y(x).

Но из уравнения xy = ex+5y − 6 мы получили y + y′x!= ex+5y (1 + 5y′)!. Значит, сюда тоже можно подставить M( − 5;1). Тогда подставим x = − 5, y = 1 в полученное уравнение. Заметим, что вместо y′!подставить нам нечего: откуда нам знать значение производной?

Итак, подставляем и упрощаем полученное выражение:

y+ y′x!= ex+5y (1 + 5y′)!.

1+ y′!( − 5) = e−5+5 (1 + 5y′)!. 1 − 5y′!= 1 + 5y′.!

y′!= 0.

Вот зачем мы дифференцировали стороны нашего уравнения: с помощью этого хода мы нашли y′!= 0, а ведь от нас требовали найти уравнение касательной.

Другими словами, нужно найти конкретные k и b для уравнения касательной

y = kx + b . Немного раньше мы вспомнили, что k = f ′(!x0), то есть k - значение

63

производной в интересующей нас точке. Мы нашли значение производной в точке

M( − 5;1): y′!= 0.

Итак, мы нашли k = 0 и b = 1, исходя из чего уравнение касательной в точке M( − 5;1) имеет вид y = 1.

Ответ: y = 1.

Для наглядности приведем рисунок, на котором изображен график функции

y = y(x), заданной уравнением xy = ex+5y − 6. Легко видеть, что касательная в точке M( − 5;1), в самом деле, является прямой y = 1.

Лиловая линия -

график функции y = y(x), заданной

уравнением

xy = ex+5y − 6.

Примечание: на рисунке хорошо видно, что для некоторых значений х существует

более одного значения у. Такие функции называются многозначными.

64

Кроме этого, иногда функция y = y(x) бывает задана параметрически. Это означает, что имеется зависимость x(t) и y(t), где t -параметр. Сразу же приведем пример, на основе которого разберемся с данной формой представления зависимости y = y(x):

(С) 3 . 52 . Напишите уравнение касательной к графику функции, заданной параметрически, в точке, соответствующей t = 2: y = 2t2 − 3t + 1, x = − t2 + 2t + 4.

Чтобы получить конкретные точки, принадлежащие графику функции y = y(x),

нужно выбрать какое-нибудь конкретное значение t и подставить его в формулы для вычисления x и y. Например, возьмем t = 0. Подставляя в формулы из «дано»,

получаем y = 1, x = 4. Таким образом, подставляя всевозможные значения параметра t, все время будем получать точки, лежащие на графике функции.

В задаче речь идет о «точке, соответствующей t = 2» . Конечно, было бы хорошо

узнать, что это за точка. Подставляем в наши формулы t = 2, получаем x = 4, y = 3. Назовем эту точку C(4;3). Вот - реальная точка на графике y = y(x), в которой нас

интересует касательная. Как и раньше, будем искать конкретные значения k и b для уравнения y = kx + b. Конечно, k = f ′(!x0), поэтому хотелось бы найти производную функции y = y(x).

Пока что мы можем найти только xt′!и yt′.!Под xt′!будем понимать производную х по t : возьмем равенство x = − t2 + 2t + 4, и продифференцируем по t (то есть будем рассматривать t как переменную, в то время как х побудет функцией). Получим:

делать? Как получить yx′!, где все будет «стандартно» : х будет переменной, а у -

функцией? Оказывается, что:

yx' = yt' xt'

Понять эту формулу довольно просто. Для начала надо задуматься о том, что именно показывает нам yx′.!Скорость роста функции? Да, но само понятие скорости относительно: как можно определить, какая скорость большая, а какая малая? Если рассматривать скорость как векторную величину (то есть сопоставлять скорости направление действия), то какая скорость положительна, а какая отрицательна? Для

65

этого надо выбрать своеобразную «точку отсчета». В случае с обычными графиками на плоскости будем мыслить себе значение производной функции y = y(x) в

определенной точке как количество раз, в которое скорость роста функции y = y(x)

превосходит скорость роста y = x.

Вспомним еще, что скорость роста функции y = y(x) в какой-нибудь конкретной точке равна скорости роста касательной, проведенной к графику y = y(x) в это

точке (в этом и есть смысл касательной).

Для наглядности рассмотрим пример: пусть у нас есть функция y = x2 − x.

Мы можем найти yx′!(т.е. - обычную производную функции y = x2 − x): yx′!= 2x − 1.

Отобразим ситуацию графически.

Итак, лиловая линия - это график функции y = x2 − x . Черная сплошная линия - очевидно, y = x . Черные линии, выполненные пунктиром - это касательные к

66

В самом деле, очевидно, что при x = 1 наша функция растет с такой же скоростью,

как и ее касательная. Сразу после момента x = 1 наша y = x2 − x начнет возрастать

касательной. В это же время, касательная в x = 1 параллельна y = x, то есть - растет с такой же скоростью, как и х. Поэтому функция y = x2 − x при x = 1 растет с такой же скоростью, что и y = x.

При x = 2, очевидно, y = x2 − x растет в три раза быстрее (смотрим на скорость роста касательной), чем y = x, поэтому y′(2)! = 3.

В конце концов, при x = 0 функция y = x2 − x убывает с такой скоростью, с которой y = x возрастает, что сказывается на знаке производной: y′(0)! = − 1 (вспомним, что функция убывает, когда производная отрицательна).

одинаковые у слева в обеих записях, во сколько раз , x2 − x (изначальная функция) растет быстрее, чем х.

Итак, yx′!- скорость у(х) относительно х. Еще проще - скорость у относительно х. Аналогично:

xt′!- скорость х относительно t (во сколько раз х быстрее, чем t).

yt′!- скорость у относительно t (во сколько раз y быстрее, чем t).

Здесь можно представить себе дорожную ситуацию: t - это грузовик, который едет со скоростью 20км/ч, пусть справа едет красная машина х со скоростью 60км/ч, и

пусть слева едет желтая машина у со скоростью 80 км/ч.

В самом деле, чтобы определить скорость желтой машины относительно красной (то есть - yx′!), нам достаточно узнать, во сколько раз желтая машина быстрее

67

грузовика, и во сколько раз красная машина быстрее грузовика, а затем первое

разделить на второе.

В нашем случае: xt′!= 60:20 = 3 (в три раза красная машина быстрее грузовика) и yt′!= 80:20 = 4 (в четыре раза желтая машина быстрее грузовика).

Отсюда мы сразу делаем вывод (на бытовом уровне), что отношение скорости

В данном случае это легко проверить, не используя в расчетах скорость грузовика:

4

yx′!= 80:60 = 3. Тем самым мы убедились в справедливости приведенной формулы.

Вернемся к нашей первоначальной задаче: y = 2t2 − 3t + 1, x = − t2 + 2t + 4.

производной yx′!именно в этой точке, подставляем вместо t в формулу конкретное значение t = 2:

4 2 − 3

k = yx′!= −2 2 + 2 = − 2,5.

Теперь мы нашли k, уже нашли интересующую нас точку C(4;3) (на странице 60),

осталось все это подставить в уравнение y = kx + b и найти значение b:

3 = − 2,5 4 + b.

Отсюда b = 13. k и b найдены. Записываем ответ: y = − 2,5x + 13.

Ответ: y = − 2,5x + 13.

68

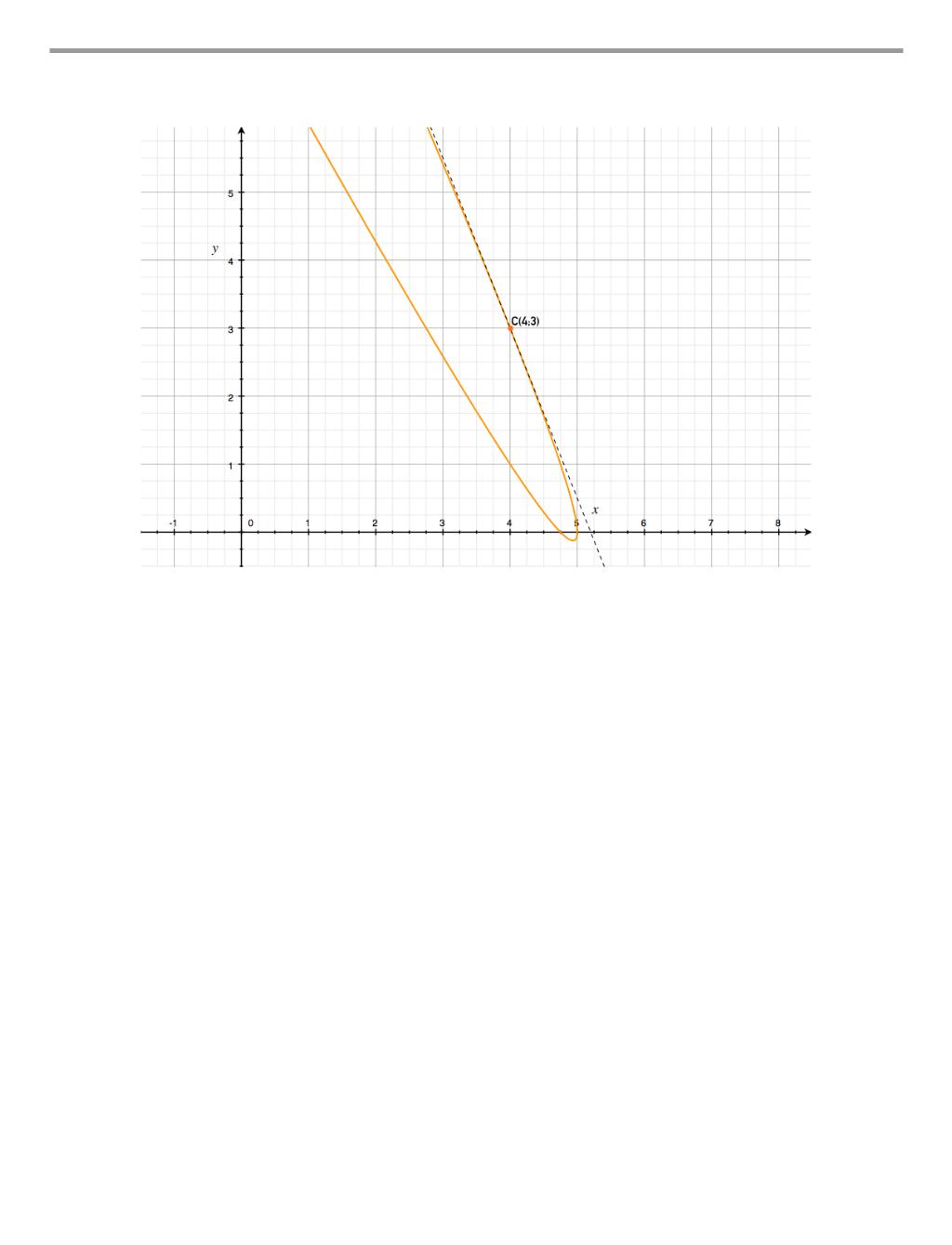
Как всегда, предлагается рассмотреть соответствующий рисунок:

69