Из уравнения (3.32) реактивный момент:

,

или

кНм.

Из уравнения (3.33):

кН.

Из уравнения (3.34) получаем 72  36  36 = 0. Следовательно, реакции M_А и R_A опоры А защемления балки по величине определены верно, направление реакции М_А необходимо изменить на обратное.

Ответ: кН;кНм.

Пример 88. Для заданной консольной балки (рис. 3.52,a) определить опорные реакции заделки.

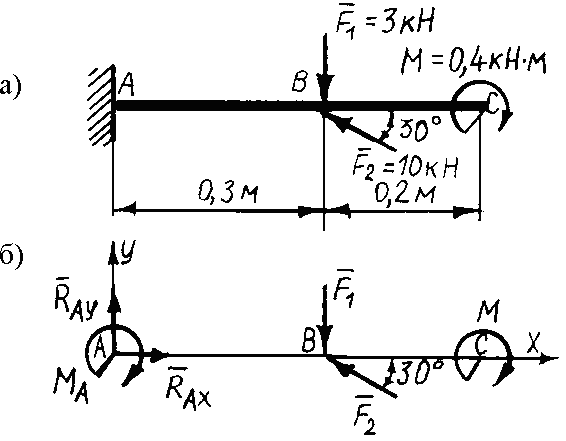
Рис. 3.52. примеру 88

Решение. Рассматриваем равновесие балки АВ. К ней приложены заданные активные силы F₁, F₂ и момент М. Рассматривая тело АВ как свободное, отбрасываем связь (заделку), заменяя ее действие реакциями  реактивным моментом M_A и составляющими реакциями R_AX и R_AY по осям координат. Расчетная схема изображена на рис. 3.52, б. Для получения плоской произвольной системы сил составляем три уравнения равновесия, выбрав в качестве центра моментов точку А (точку пересечения двух неизвестных сил):

1).

откуда кНм.

2).

3).

Составляем проверочное уравнение равновесия:

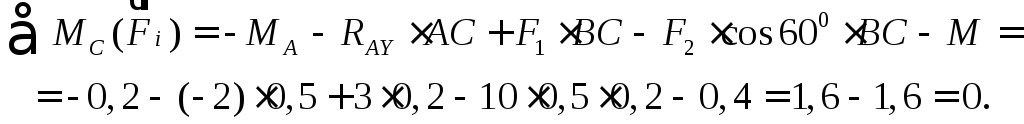
Следовательно, реакции определены верно. Реакция R_AY получилась отрицательной, значит, ее действительное направление противоположно предварительно выбранному. Примененная система уравнений равновесия наиболее целесообразна при рассмотрении равновесия любых консольных балок.

Полная реакция опоры :

кН.

Ответ: кН;кНм.

Пример 89. Определить реакции опор балки (рис. 3.53), если  кН,  кН,  кНм, кНм, кН/м, кН/м.

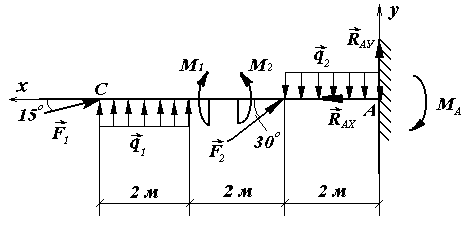
Рис. 3.53. К примеру 89

Решение. Рассматриваем равновесие балки СА. К ней приложены заданные сосредоточенные силы F₁, F₂, равномерно распределённые нагрузки q₁, q₂ и моменты M₁, M₂. Рассматривая тело СА как свободное, отбрасываем связь (заделку), заменяя ее действие реакциями  реактивным моментом M_A и составляющими реакциями R_AX и R_AY по осям координат. Расчетная схема изображена на рис. 3.53. Для получения плоской произвольной системы сил составляем три уравнения равновесия, выбрав в качестве центра моментов точку А (точку пересечения двух неизвестных сил):

Отсюда:

кНм;

кН;

кН.

Составляем проверочное уравнение равновесия:

Значит, реакции определены верно. Реакция R_AY и реактивный момент M_A получились отрицательными, следовательно, их действительные направления противоположны предварительно выбранным.

Полная реакция опоры :

;

кН.

Ответ: кН;кНм.

Пример 90. Механизм манипулятора, состоящий из трёх звеньев, соединённых шарнирами, в положении равновесия расположен в вертикальной плоскости (рис. 3.54, а).

Длины и массы звеньев: l₁ = 1,2 м; l₂ = 0,7 м; m₁ = 55 кг; m₂ = 40 кг; углы ₀₁ = /3, ₁₂ = /6. Найти моменты сил приводов в шарнирах А и В, если рука ВС манипулятора удерживает деталь, масса которой m = 30 кг. Звенья считать однородными стержнями.

Решение. На звенья манипулятора действуют силы тяжести G₁, G₂, приложенные в середине звеньев 1 и 2, сила тяжести детали G, приложенная в точке С звена 2 (рис. 3.54, б). Все силы направлены вертикально вниз.

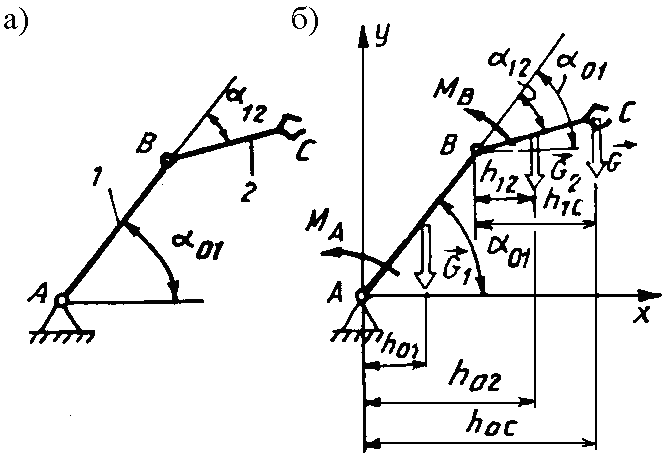
Рис. 3.54. К примеру 90

Сначала вычислим проекции звеньев на ось Ах:

м;

м.

Моменты сил приводов в шарнирах:

;

Нм;

;

;

Нм.

Моменты М_А и М_В – это реактивные моменты, направленные против хода часовой стрелки.

Ответ: Нм; Нм.

Пример 91. Пример имеет своим прототипом схему подъема мачтовых опор ЛЭП с помощью тягачей (рис. 3.55).

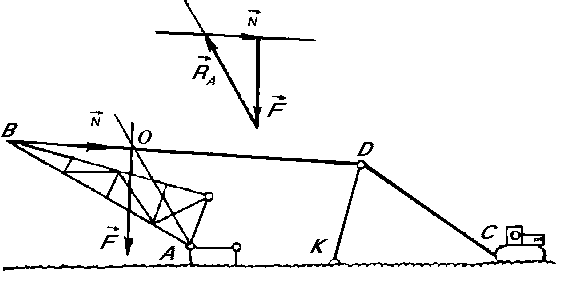
Рис. 3.55. К примеру 91

Рассмотрим эту схему.

Мачта АВ, лежащая возле заранее подготовленного фундамента, соединяется с ним шарниром А. Затем с помощью канатной тяги ВDС она поднимается до вертикального положения. При этом вспо-

могательная штанга КD облегчает работу в начальной стадии подъема, отводя направление тяги несколько вверх. Здесь осуществляется типичный случай равновесия трех сил, расположенных в одной плоскости (в данном случае - в вертикальной). Эти силы сходятся в некоторой точке О, определяемой пересечением каната с линией силы тяжести мачты. Искомая реакция также выходит на эту точку.

Графическое решение задачи состоит в том, что считая силу тяжести мачты, а также ее угол и угол каната с горизонтом известными, необходимо построить на векторе F в определенном масштабе замкнутый силовой треугольник при точке О, которую выгодно вынести в сторону от основного чертежа. Стороны треугольника должны быть строго параллельны направлениям искомых сил, тогда величины этих сил будут найдены прямым измерением сторон треугольника в миллиметрах и умножением их на выбранный масштаб.

Аналитическое решение задачи состоит в использовании уравнений равновесия, система которых для произвольных сил на плоскости имеет вид:

;

; (3.35)

Решение показано на несколько видоизмененной схеме (рис. 3.56).

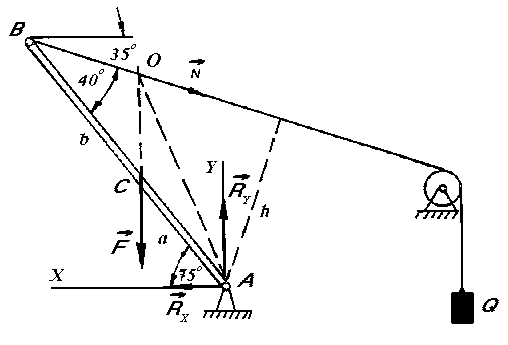
Рис. 3.56. К примеру 91

Пусть мачта АВ в данный момент подъема составляет с горизонтом угол, равный 75°, а тяга ВК наклонена к горизонту под углом 35°. Угол между мачтой и канатом получается равным 40°. Пусть центр тяжести С делит длину мачты на отрезки а = 7 м и b = 12 м. Вес мачты Н (масса  14 т). Требуется определить силу N натяжения каната и реакцию опоры .

Решение. За начало координат принять шарнир А, направив ось Х в сторону наклона мачты, а ось Y  вверх. Тогда уравнение моментов примет вид

(3.36)

где (плечо силы N относительно центра моментов А).

Отсюда

Н.

Уравнения проекций сил на координатные оси:

;

(3.37)

,

откуда

Н;

Н.

Положительные значения реакций указывают на то, что их направления на чертеже выбраны верно (не забудьте, что ось Х здесь направлена влево!).

Полная реакция шарнира R_A:

;

Н.

Её угол с горизонтом легко определяется по тангенсу.

Для проверки решения нужно убедиться, что линия действия реакции R_A действительно выходит на точку пересечения линий сил F и N.

Ответ: Н;Н.

Пример 92. Пластинка ОА, поворачиваясь относительно оси шарнира О, может устанавливаться под любым углом к горизонту (рис. 3.57, а). На пластинке лежит тело В весом G. Определить наибольший угол  наклона пластинки, при котором тело будет оставаться в равновесии.

а) б)

Рис. 3.57. К примеру 92

Решение. Примем систему координат Оху. На тело В действуют сила тяжести G, нормальная реакция R и сила трения F_f (рис. 3.57, б).

Составим уравнения равновесия тела:

; ;

; ,

из которых найдём

.

Заметим, что отношение силы трения F_f к нормальной реакции R есть коэффициент трения f. Тогда угол  будет углом трения : f = tg. Таким образом, для равновесия тела необходимо, чтобы выполнялось условие   .

С помощью рассматриваемого простого устройства можно экспериментально определять коэффициенты трения скольжения.

Например, в момент начала движения стального бруска по стальной пластине следовательно, коэффициент трения стали по стали

Ответ:

Пример 93. Груз весом G = 280 Н подвешен в точке Е горизонтальной балки АВ весом G₁ = 160 H. Балка АВ укреплена при помощи шарнира А и свободно опирается концом В на балку СD весом G₂ = 120 H. Балка CD имеет шарнир С и концом D опирается на гладкую вертикальную стену. Расстояние АЕ = 1/4 АВ; CB = 1/3 CD. Определить реакции опор A, C и D (рис. 3.58).

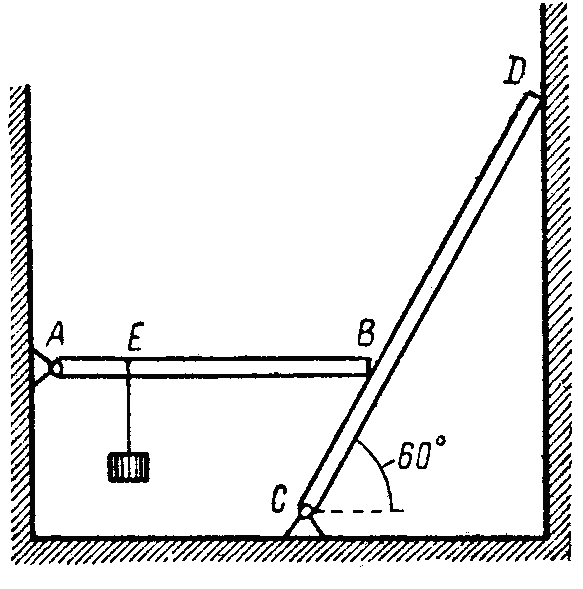
Рис. 3.58. К примеру 93

Решение. Реакции шарниров А и С, не известные по направлению, разложим на составляющие R_AX, R_AY, R_CX, R_CY. Реакция стены R_D направлена перпендикулярно к ней (рис. 3.59, a). Пять неизвестных величин R_AX, R_AY, R_CX, R_CY, R_D нельзя определить из системы трех уравнений равновесия. Поэтому произведем расчленение балок, т. е. рассмотрим отдельно равновесие сил, приложенных к каждой из балок.

На балку АВ действуют заданные силы веса G и G₁, составляющие R_AX, R_AY реакции шарнира А и реакция R_B балки CD, направленная по нормали к ее поверхности (рис. 3.59, б).

а) б)

Рис. 3.59. К примеру 93

На балку CD действуют вес балки G₂, приложенный в середине CD, реакция балкиАВ, равная по модулю реакции R_B и противоположная ей, составляющие R_CX, R_CY реакции шарнира С и реакция стены R_D.

Составим по три уравнения равновесия сил, действующих на каждую балку, и определим шесть неизвестных величин R_AX, R_AY, R_CX, R_CY, R_D, .

Для сил, приложенных к балке АВ, получим:

;;

; ; (3.38)

; .

Для сил, приложенных к балке CD:

;

; (3.39)

;

.

Из системы уравнений (3.38) имеем:

Н;

Н;

Н.

Так как , из системы уравнений (3.39) следует, что

Н;

Н;

Н.

Знаки в ответах показывают, что сила R_CX направлена влево, а действительные направления остальных сил совпадают с указанными на схеме.

Полная реакция опоры :

;

Н.

Полная реакция опоры :

;

Н.

Ответ: Н;Н;Н.

Пример 94. Две балки АВ и ВС одинаковой длины l = 3 м соединены между собой шарниром В (рис. 3.60, а). Конец А балки АВ заделан в вертикальной стене, а конец С балки ВС опирается на подвижную опору, расположенную под углом ₁ = 30 к оси балки ВС. На балку АВ по всей её длине действует равномерно распределённая нагрузка интенсивностью q = 3 кH/м. На балку ВС действует сила F = 10 кH, приложенная в середине балки под углом  = 60 к её оси. Определить реакции опор А и С, а также в шарнире В, пренебрегая силами тяжести балок.

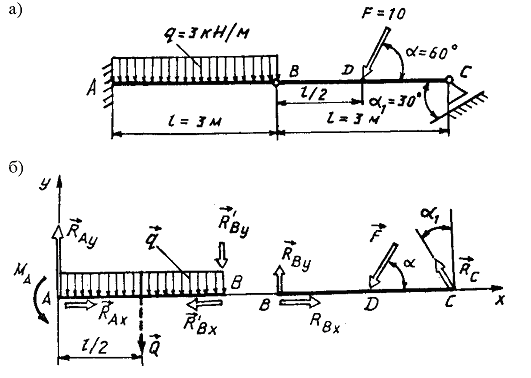
Рис. 3.60. К примеру 94