
Механика1
.pdfМинистерство образования Республики Беларусь Белорусский национальный технический университет Кафедра технической физики
ФИЗИЧЕСКИЕ ОСНОВЫ КЛАССИЧЕСКОЙ МЕХАНИКИ
Методическое пособие по физике для студентов дневной и заочной формы обучения
Минск 2003
УДК (53 075.4) ББК 22.3 я 73 М 54
Составители: В.И. Кудин, М.Б. Ржевский
Рецензент: В.А. Самойлюкович, кафедра физики, БНТУ
В методическом пособии рассмотрены физические основы классической механики в объеме первых пяти лекций по первой части курса общей физики «Механика и молекулярная физика». Изложенный материал имеет конспективный характер и может оказать помощь студентам первого курса в освоении лекционного материала, а также в подготовке к выполнению лабораторных работ физического практикума по данному разделу физики.
2
|
|
Оглавление |
|
Физические основы классической механики................................ |
4 |
||
1. |
Кинематика материальной точки .............................................................. |
4 |
|
|
Скорость при криволинейном движении материальной точки....... |
5 |
|
|
Ускорение при криволинейном движении материальной точки ..... |
6 |
|
2. |
Кинематика вращательного движения твердого тела.............................. |
9 |
|
3. |
Динамика материальной точки................................................................ |
12 |
|
4. |
Закон сохранения импульса системы материальных точек.................. |
14 |
|
|
Центр масс системы материальных точек и его свойства............ |
16 |
|
5. |
Движение тела с переменной массой. Реактивное движение............... |
16 |
|
|
Уравнение Циолковского........................................................................ |
17 |
|
6. |
Динамика вращательного движения твердого тела............................... |
18 |
|
|
Момент импульса материальной точки относительно оси |
|
|
|
вращения................................................................................................... |
18 |
|
7. |
Момент импульса твердого тела относительно неподвижной оси. |
|
|
Момент инерции твердого тела................................................................... |
20 |
||
|
Вычисление моментов инерции некоторых тел правильной формы |
||
|
Момент....................................................................................................................инерции тела относительно нецентральной оси. |
21 |
|
|
|
||
|
Теорема Штейнера................................................................................. |
22 |
|
|
Главные оси и главные моменты инерции.......................................... |
23 |
|
8. |
Основной закон динамики вращения твердого тела.............................. |
25 |
|
|
Аналогия между поступательным и вращательным движением.26 |
||
9. |
Гироскопы ................................................................................................. |
26 |
|
10. |
Механическая работа и мощность......................................................... |
28 |
|
11. |
Механическая энергия............................................................................ |
30 |
|
12. |
Закон сохранения полной механической энергии системы |
|
|
материальных точек...................................................................................... |
32 |
||
13. |
Связь между потенциальной энергией и консервативной силой....... |
33 |
|
14. |
Потенциальная энергия упругой деформации ..................................... |
34 |
|
15. |
Потенциальные кривые. Потенциальные ямы и барьеры. Движение |
|
|
материальной точки в потенциальной яме................................................. |
35 |
||
16. |
Законы сохранения в механике и симметрии пространства и времени |
||
........................................................................................................................ |
|
|
36 |
17. |
Закон сохранения момента импульса системы материальных точек.37 |
||
18. |
Движение тела в центральном гравитационном поле ......................... |
38 |
|
|
Законы Кеплера........................................................................................ |
43 |
|
Литература..................................................................................................... |
44 |
||
3
Физические основы классической механики
Классическая механика или механика Ньютона есть наука о движении и равновесии тел. Под движением в механике понимается перемещение тел или их частей друг относительно друга. Механику можно разделить на три раздела: кинематику, динамику и статику.
Кинематика изучает движение тел, не интересуясь причинами, обуславливающими это движение.
Динамика изучает движение тел в связи с теми причинами (взаимодействиями между телами), которые обуславливают тот или иной характер движения.
Статика изучает условия равновесия тел под действием сил.
Если мы собираемся изучить движение какого-либо тела, то обязательно нужно указать, по отношению к каким другим телам происходит данное движение. Кроме того, для описания движения необходимо также определять время. Это делается с помощью любого периодического процесса (в частности, с помощью часов).
Система отсчета – это совокупность тела отсчета, системы координат (например, декартовой), связанной с телом отсчета, и выбранного способа измерения времени (часы).
1. Кинематика материальной точки
Материальная точка – это тело, размерами которого в условиях данной задачи можно пренебречь. При движении такого тела можно считать, что все вещество тела как бы сосредоточено в одной геометрической точке. Материальная точка есть идеализированный образ реально существующих тел. Вопрос о том, можно ли данное конкретное тело рассматривать как материальную точку или нет, зависит не от размеров этого тела, а от условий задачи. Одно и тоже тело в одних случаях может рассматриваться как материальная точка, в других же случаях должно рассматриваться как протяженное тело. Например, Землю при рассмотрении ее орбитального движения вокруг Солнца с большой точностью можно принять за материальную точку. Но эта идеализация не годиться при рассмотрении вращения Земли вокруг собственной оси, ибо бессмысленно говорить о вращении геометрической точки вокруг оси, проходящей через эту точку.
Материальная точка при своем движении описывает некоторую линию, которая называется траекторией. В зависимости от формы траектории различают прямолинейное движение и криволинейное движение. Основными понятиями в кинематике являются: путь и перемещение.
Путь s - это расстояние между точками 1 и 2, отсчитанное вдоль траектории (рис. 1.1). Путь s - величина скалярная.
→
Перемещение ∆ r - это вектор, проведенный из точки 1 в точку 2. Пе-
→ |
|
|
|
|
|
|
|
|
ремещение ∆ r - величина векторная. |
|
|
|
|
|
|
|
|
|
Путь и перемещение в СИ |
|||||||
|
измеряются в метрах (м). |
|
|
|||||
|
Следует заметить, |
что в общем |
||||||
|
|
|
|
→ |
|
|
|
|
|
случае |
s ≠| ∆ r | , |
|
но |
|
если |
||
|
материальная |
точка |
движется |
по |
||||
|
прямой |
и |
в |
одну |
сторону, |
|||
|
|
→ |
|
|
|
|
|
|
|
тоs =| ∆ r | . |
|
Это |
|
можно |
|||
Рис. 1.1 |
проиллюстрировать |
|
следующими |
|||||
|
примерами: |
|
|
|
|
|
|
|
1. Материальная точка движется по окружности радиуса R, |
и совершила |
|||||||
один оборот. При этом |
перемещение |
точки |
→ |
|
0, |
а |
путь |
|
∆ r = |
||||||||
s = 2πR ≠ 0 .
4

→
2.Тело брошено вертикально вверх. Пока тело движется вверх s =| ∆ r | , но для моментов времени, когда тело при своем движении начнет па-
→
дать вниз, путь его становится больше модуля перемещения s >| ∆ r | .
Существует три способа описания движения материальной точки: координатный, векторный и естественный.
1) Координатный способ:
Если с системой отсчета связать декартову систему координат (X, Y, Z) (рис. 1.2) , то положение материальной точки А можно задать с помощью координат (x, y, z). Траекторию движения мы определим, если будем знать функции:
Рис. 1.2 |
x = x(t), y = y(t), z = z(t). |
|
2) Векторный способ: |
||
|
||
|
→ |
В этом случае положение точки А будет определяться вектором r , про-
→
веденным из начала отсчета О в данную точку А. Этот вектор r называется радиус–вектором точки А. Траектория движения будет определяться
→ →
функцией r = r (t) . Как мы видим, векторный способ описания движения более экономный, поскольку требует определения одной функции
→ |
→ |
r |
= r (t) , правда, векторной функции от времени t. |
Для того, чтобы установить связь между этими двумя способами описа-
|
|
|
→ → → |
ния, введем три единичных вектора, орты |
i , j, k , направленных вдоль |
||
осей X, Y, Z, соответственно. Тогда, как видно из рис. 1.2, |
|||
→ |
→ |
→ |
→ |
r |
= x i |
+ y j + z k , |
|
→ |
|
|
|
а модуль радиус–вектора r |
равен |
|
|
r = x2 + y2 + z 2 . |
|||
3) Естественный способ:
При естественном способе описания движения материальной точки, необходимо знать траекторию движения материальной точки. Тогда положение точки на траектории в разные моменты времени будет задаваться функцией пути от времени: s = s(t).
Скорость при криволинейном движении материальной точки
→
Пусть материальная точка движется по траектории r (t), и пусть в мо-
→
мент времени t она находится в точке 1, описываемой радиус-вектором r1
(рис. 1.3). Рассмотрим достаточно близкий следующий момент времени t +
∆t.
Вэтот момент времени материальная точка находится в точке 2, и положе-
→→ → →
∆r = r2 −r1 , будет пере-
→
мещение материальной точки за время ∆t, величина ∆ r будет представ-
∆t
лять среднюю скорость перемещения точки на участке траектории 1→2, а
5
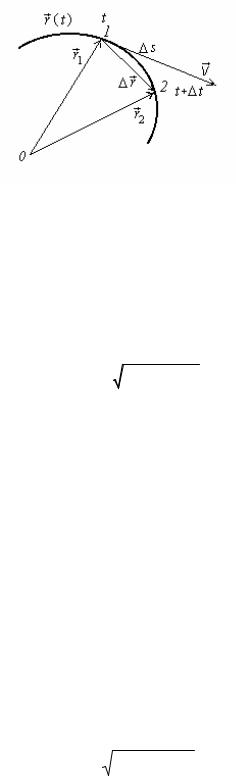
∆s
величина ∆t – среднюю путевую скорость точки. Мгновенная скорость
→
v материальной точки равна
Рис. 1.3
|
→ |
→ |
• |
, |
v = lim ∆ r |
= d r |
= r |
||
→ |
|
|
→ |
|
∆t→0 ∆t |
dt |
|
|
|
|
→ |
|
|
|
где под |
v подразумевается |
|||
мгновенная |
скорость |
в |
||
данной |
точке |
траектории. |
||
Эта формула справедлива и
для |
прямолинейного |
||
движении |
|
материальной |
|
точки. |
|
|
|
Как видно |
из |
рис. 1.3, |
|
|
→ |
|
|
скорость |
v |
направлена по |
|
касательной |
к траектории. |
||
Далее при |
∆t→0 |
∆r→ ∆s, |
|
имодуль скорости v равен производной от пути по времени
v= dsdt .
→
Как всякий вектор, вектор скорости v можно выразить через его проекции на оси координат:
→ |
→ |
+v y |
→ |
→ |
• → |
• → |
• → |
v |
=vx i |
j |
+vz k |
= x i |
+ y j |
+ z k |
|
|
|
|
|
|
|
|
. |
v = vx2 +v y2 +vz2
Скорость v в СИ измеряется в метрах в секунду (м/с).
Ускорение при криволинейном движении материальной точки
В механике вводится еще одна важная характеристика движения – ус-
→ →
корение a , т.е. скорость изменения вектора скорости v во времени. Сред-
|
|
→ |
|
|
|
|
→ |
>= ∆v |
|
|
|
|
|
нее ускорение < a |
, а мгновенное ускорение материальной точки |
|||||
равно |
|
∆t |
|
|
|
|
|
|
→ |
→ |
|
|
|
|
a |
|
• |
•• |
||
|
= lim ∆v |
= d v |
= v = r . |
|||
|
→ |
|
|
|
→ |
→ |
|
|
∆t→0 ∆t |
dt |
|
→ |
|
|
|
|
→ |
|
|
|
Учитывая определение скорости v , мгновенное ускорение a есть вто-
→
рая производная от радиус-вектора r по времени t (две точки означают вторую производную по времени t). Ускорение a в СИ измеряется в метрах на секунду в квадрате (м/с2).
Легко установить связь с координатным представлением ускорения:
→ |
→ |
→ |
→ |
•• → |
•• → |
•• → |
a |
= ax i |
+ ay j |
+ az k |
= x i |
+ y j |
+ z k |
|
|
|
|
|
|
. |
a = ax2 + a2y + az2
Особенно удобен естественный способ представления ускорения.
6
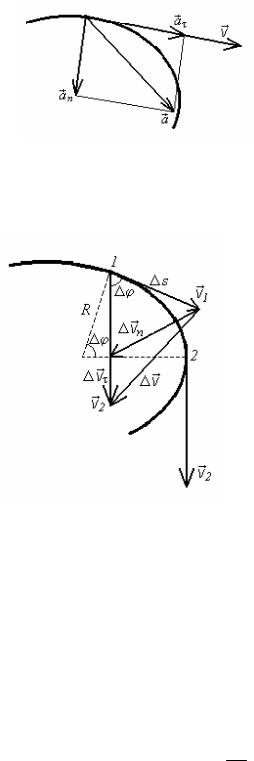
В общем случае криволинейного движения мгновенное ускорение |
→ |
a |
|
→ |
→ |
направлено под некоторым углом к скорости v . Представим вектор |
a в |
виде суммы двух векторов, один из которых направлен вдоль вектора ско-
→
рости v , т.е. по касательной к траектории, а второй по нормали к траекто-
|
|
|
|
|
|
|
рии в этой точке: |
|
|
|||
|
|
|
|
|
|
|
|
→ |
→ |
→ |
|
|
|
|
|
|
|
|
|
|
a = a τ |
+ a n . |
|
||
|
|
|
|
|
|
|
Эти две составляющие |
|
||||
|
|
|
|
|
|
|
ускорения имеют |
|
|
|||
|
|
|
|
|
|
|
специальные названия: |
|
||||
|
|
|
|
|
|
|
→ |
|
|
|
|
|
|
|
|
|
|
|
|
a τ – вектор |
|
|
|
||
|
|
|
|
|
|
|
тангенциального ускорения, |
|||||
|
Рис. 1.4 |
|
|
|
→ |
|
|
|
|
|
||
|
|
|
|
a n - вектор нормального |
||||||||
|
|
|
|
|
|
|
ускорения. |
|
|
|
|
|
|
|
|
|
|
|
|
|
→ |
→ |
|
|
|
Приступим теперь к определению величин векторов a τ |
и a n . Для этого |
|||||||||||
|
|
|
|
|
нарисуем |
траекторию |
движения |
|||||
|
|
|
|
|
→ |
|
|
|
|
|
|
|
|
|
|
|
|
r (t) и снова |
выберем |
два |
|||||
|
|
|
|
|
близких момента времени t и t + |
|||||||
|
|
|
|
|
∆t (рис. 1.5). |
|
|
|
|
|||
|
|
|
|
|
В момент времени t материальная |
|||||||
|
|
|
|
|
точка |
находилась в |
точке 1, и |
|||||
|
|
|
|
|
|
|
|
|
|
|
→ |
|
|
|
|
|
|
скорость ее равнялась v1 , а в |
|||||||
|
|
|
|
|
момент времени |
t + ∆t |
- в точке |
|||||
|
|
|
|
|
|
|
|
|
|
|
→ |
|
|
|
|
|
|
2, и скорость ее равнялась v 2 . За |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
→ |
|
|
|
|
|
время |
∆t |
вектор |
скорости |
v |
|||
|
|
|
|
|
изменился как по модулю, так и |
|||||||
|
|
|
|
|
по направлению. Для того чтобы |
|||||||
|
|
|
|
|
|
|
|
|
→ |
|
|
|
|
|
|
|
|
определить |
∆v , |
перенесем |
|||||
|
|
|
|
|
|
|
→ |
|
|
|
|
|
|
Рис. 1.5 |
|
|
|
вектор v 2 |
в точку 1 и представим |
||||||
|
|
|
|
→ |
|
|
|
|
|
|
|
|
→ |
→ |
|
|
|
∆v в виде суммы двух векторов |
|||||||
|
|
|
|
|
|
|
|
|
|
|
||
∆v n |
и ∆vτ . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
→ |
→ |
→ |
|
|
|
|
|
|
|
|
|
|
∆v = ∆vτ +∆v n . |
|
|
|
|
|
||||
При этом модуль вектора ∆vτ =v2 −v1 . |
|
|
|
|
|
|
|
|||||
Согласно определению ускорения: |
|
|
|
|
|
|
|
|
||||
|
|
→ |
|
→ |
|
|
→ |
|
|
|
|
|
|
→ |
∆v |
= lim |
∆vτ |
+ lim |
∆v n |
→ |
→ |
|
|
|
|
|
a = lim |
= aτ + an . |
|
|
||||||||
|
∆t→0 |
∆t |
∆t→0 |
∆t |
∆t→0 |
∆t |
|
|
|
|
|
|
→
1)Как видно из построения, ∆vτ = ∆v , и модуль вектора a τ равен производной от модуля вектора скорости, т.е.
aτ = ddtv .
7

→
2) Для нахождения модуля вектора a n , сделаем дополнительные по-
строения (см. рис. 1.5), а именно, в точках 1 и 2 проведем нормали к траектории и будем считать достаточно малый участок кривой 1–2 ду-
гой окружности радиуса R . Тогда ∆s = R∆ϕ , откуда следует, что
∆ϕ = ∆Rs .
→
Зная угол ∆ϕ, найдем модуль вектора ∆v n :
∆vn |
=v1∆ϕ = |
v1∆s |
. |
|
|||||
|
|
||||||||
|
|
|
|
|
R |
|
|
||
Возвращаясь к определению |
an , находим |
|
|
||||||
an = lim |
∆v |
n |
= lim |
v |
∆s |
= |
v 2 |
||
|
|
1 |
|
|
1 |
||||
∆t→0 |
|
∆t |
∆t→0 |
R∆t |
|
R |
|||
an = vR2
где под v понимается мгновенная скорость в данной точке траектории. Рассмотрим два частных случая:
1)Равномерное движение материальной точки по окружности: v = const.
Тогда тангенциальное ускорение равно нулю и полное ускорение равно нормальному, т.е. центростремительному ускорению:
aτ = ddtv = 0
a = an = vR2
2) Прямолинейное движение материальной точки:
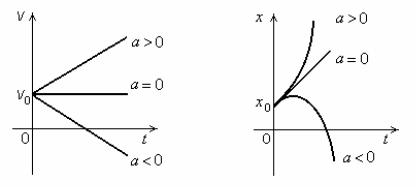
В этом случае радиус кривизны траектории равен бесконечности и нормальное ускорение равно нулю. Полное ускорение равно тангенциальному и направлено вдоль направления движения, а именно, если а > 0, по направлению движения, если а < 0, против направления движения.
R = ∞ a |
|
= |
v 2 |
|
= |
dv |
|
n |
|
= 0, a = a |
|
||||
|
|
R |
|
τ |
dt |
||
|
|
|
|
|
|
||
Рассмотрим прямолинейное равноускоренное движение материальной точки, т.е. движение, при котором ускорение точки остается постоянным. Координатную ось X выберем вдоль прямой, по которой движется точка. Тогда из формулы
a = dv dv = a dt . |
|
dt |
|
Интегрирование последнего уравнения при a = const дает |
|
v =v0 +a t , |
(1.1) |
где v0 – начальная скорость точки, т.е. скорость точки в момент времени t = 0. В этой формуле v - проекция вектора скорости на ось X.
Далее из определения
v = dxdt dx =v dt =v0dt +atdt .
Интегрирование этого выражения приводит к формуле для координаты точки
x = x0 +v0t + a2t2 ,
8
где x0 – начальная координата точки. Выбирая ее равной нулю, получим
s =v0t + |
a t |
2 |
|
2 |
. |
(1.2) |
|
|
|
|
Однако заметим, что это формула для перемещения точки, а не для пути. Исключая из формул (1.1) и (1.2) время t, получим полезную формулу для зависимости s = f(v)
s = |
v 2 |
−v 2 |
, или v 2 −v02 = 2 a s . |
|
0 |
||
|
|
2a |
|
Рис. 1.6
В заключение приведем графики скорости и координаты точки при прямолинейном равноускоренном движении (рис. 1.6).
2. Кинематика вращательного движения твердого тела
Абсолютно твердым телом или просто твердым телом в механике называют идеализированную систему материальных точек, все расстояния между которыми остаются неизменными при движении этой системы как целого в пространстве и времени. Реальные тела можно приближенно рассматривать как абсолютно твердые тела, если деформации, возникающие под действием внешних сил, малы и при решении поставленной задачи о движении твердого тела не учитываются.
Всякое движение твердого тела можно разложить на два основных вида движения – поступательное и вращательное.
Поступательное движение - это такое движение, при котором любая прямая, связанная с движущимся телом, остается параллельной самой себе.
Вращательное движение – это такое движение, при котором все точки тела движутся по окружностям, центры которых лежат на одной и той же прямой, называемой осью вращения. Ось вращения может находиться и вне тела.
Вращение твердого тела описывается углом поворота ϕ(t), на который повернулось тело за время t. Поворот тела на некоторый угол ϕ можно задать в виде отрезка, длина которого равна ϕ, а направление совпадает с осью, вокруг которой производится поворот. Направление поворота и изображающего его отрезка связывается правилом правого винта, т.е. направление отрезка должно быть таким, чтобы, глядя вдоль него, мы видели поворот совершающимся по часовой стрелке. Повороты на конечные углы складываются не по правилу параллелограмма и поэтому не являются векторами. Иначе обстоит дело для поворотов на очень малые углы ∆ϕ. В этом случае два совершаемых последовательно малых поворота ∆ϕ1 и ∆ϕ2 обуславливают такое же перемещение любой точки тела, как и поворот ∆ϕ3, получаемый из ∆ϕ1 и ∆ϕ2 сложением по правилу параллелограмма, т.е.
очень малые повороты можно рассматривать как векторы ∆→ϕ, и в нашем случае
9
∆→ϕ3 = ∆→ϕ1 + ∆→ϕ2 .
Введем следующие понятия:
|
→ |
|
|
|
|
→ |
∆ϕ |
|
|
|
|
среднюю угловую скорость < ω>= |
, и мгновенную угловую скорость |
||||
вращающегося твердого тела |
∆t |
|
|
|
|
→ |
|
→ |
|
||
→ |
|
|
|||
∆ϕ |
|
dϕ |
|
||
ω = lim |
= |
, |
|||
∆t |
dt |
||||
∆t→0 |
|
|
|||
где ∆t - время, за которое совершается поворот ∆→ϕ. Угловая скорость ω в
СИ измеряется в радианах в секунду (рад/с).
→
Угловая скорость ω направлена вдоль оси, вокруг которой вращается тело, в сторону, определяемую правилом правого винта. Модуль угловой
скорости равен ω = ddtϕ .
Вращение с постоянной угловой скоростью называется равномерным вращением. Если вращение является равномерным, то ω = ϕt , где ϕ - ко-
нечный угол поворота за время t. Равномерное вращение можно характеризовать периодом обращения T - временем, в течение которого тело делает один оборот, т.е. поворачивается на угол 2π.
Тогда |
ω = |
2π |
, |
откуда T = |
2π |
. |
T |
|
|||||
|
|
|
|
ω |
||
Число оборотов единицу времени или частота вращения n равна:
n = T1 = 2ωπ ω = 2πn - связь угловой скорости с час-
тотой вращения.
В СИ величина Т измеряется в секундах (с), а n – в оборотах в секунду (с-1).
→
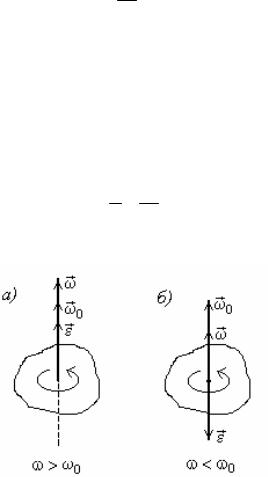
Вектор ω может изменяться как за счет изменения скорости вращения тела вокруг оси, так и за счет поворота оси вращения в пространстве. Пусть за время ∆t
→
вектор ω получает при-
→
ращение ∆ω. Изменение вектора угловой скорости со временем ха-
Рис. 2.1 рактеризуется величиной, которая называется
→
угловым ускорением ε и определяется следующим образом:
→
→ ∆ω
среднее угловое ускорение < ε >= ∆t , и мгновенное угловое ускорение вращающегося твердого тела
10
