
- •Глава 4. Пространственная система сил (ПрСс)
- •4.1. Момент силы относительно оси Величина, равная проекции на ось вектора момента силы (рис. 4.1) относительно любой точки, принадлежащей данной оси, называется моментом силы относительно оси.
- •4.2. Приведение силы к центру
- •4.3. Равновесие твёрдых тел под действием пространственной системы сил
- •Примеры
- •Задачи к заданиям
- •Литература
Глава 4. Пространственная система сил (ПрСс)
4.1. Момент силы относительно оси Величина, равная проекции на ось вектора момента силы (рис. 4.1) относительно любой точки, принадлежащей данной оси, называется моментом силы относительно оси.

Рис. 4.1. Момент силы относительно оси
Моменты сил относительно координатных осей вычисляются по формулам
![]() ;
;
![]() ;
;
![]() (4.1)
(4.1)
В практике решения задач необходимо помнить, что моментом силы относительно оси называется произведение проекции силы на плоскость, перпендикулярную оси, на плечо. Плечом проекции силы называется перпендикуляр, проведённый из точки пересечения оси с плоскостью, на проекцию силы или её продолжение. Момент силы относительно оси считается положительным, если плоскость под действием проекции силы стремится повернуться в направлении против хода часовой стрелки (если смотреть на плоскость со стороны стрелки оси), и отрицательным, если в направлении часовой стрелки.
Момент силы относительно оси равен нулю в двух случаях:
1. Если линия действия силы параллельна оси (проекция силы на плоскость обращается в нуль);
2. Если сила или линия действия силы пересекает ось (плечо проекции силы равно нулю).
Для вычисления момента силы, например, относительно оси ОZ, необходимо:
1. Провести в любом месте плоскость XOY, перпендикулярную к оси OZ, и найти точку пересечения этой плоскости с осью;
2. Спроецировать силу F на эту плоскость и определить вектор FXY;
3. Опустить из точки пересечения оси с плоскостью перпендикуляр на линию действия FXY и найти его длину h;
4. Вычислить
произведение
![]() ;
;
5. Определить знак
момента
![]() .
.
4.2. Приведение силы к центру
Всякую силу F, приложенную к твёрдому телу в точке А, можно переносить параллельно линии её действия в любую точку О, присоединив пару сил, момент которой равен моменту данной силы относительно новой точки её приложения.
Докажем эту теорему. Пусть в точке А твёрдого тела приложена сила F (рис. 4.2, а). Выберем произвольную точку О (точку приведения), не лежащую на линии действия силы F. Приложим в точке О параллельно данной силе F две равные по модулю, но противоположные по направлению силы F и F (рис. 4.2, б). Полученная система сил (F, F, F) эквивалентна одной силе F.
Силы F
и F
образуют пару (F,
F).
Следовательно, система сил (F,
F,
F)
эквивалентна силе F,
приложенной в точке О
и равной по модулю силе F,
и паре сил (F,
F)
с моментом
![]() (рис. 4.2, в).
(рис. 4.2, в).

а) б) в)
Рис. 4.2. Приведение силы к центру
4.3. Равновесие твёрдых тел под действием пространственной системы сил
Для равновесия тела при действии на него любой пространственной системы сил необходимо и достаточно, чтобы главный вектор и главный момент этой системы сил были равны нулю:
![]() ;
;
![]() .
(4.2)
.
(4.2)
В проекциях на координатные оси уравнения равновесия (4.2) твёрдого тела можно записать в виде следующих шести уравнений:


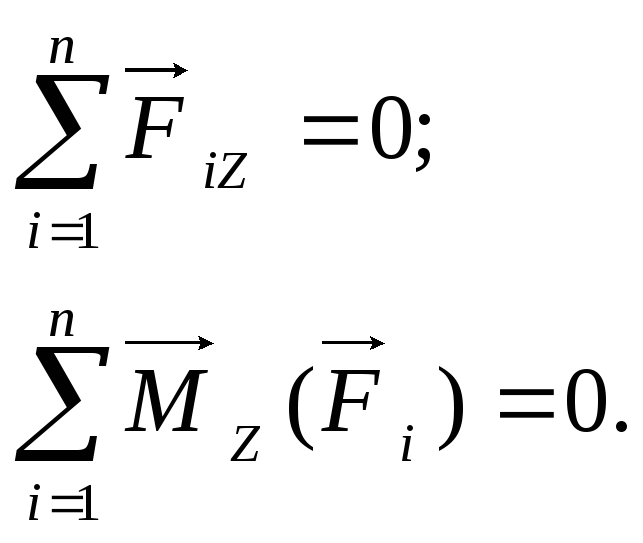 (4.3)
(4.3)
Для равновесия тела в случае действия на него произвольной пространственной системы сил необходимо и достаточно, чтобы суммы проекций всех сил на каждую из осей и суммы моментов этих сил относительно координатных осей были равны нулю.
Пространственная
система параллельных сил.
Если OZ
параллельна линиям действия сил (рис.
4.3), то проекции сил
![]() на осиOX
и OY,
а также моменты
на осиOX
и OY,
а также моменты
![]() относительно осиOZ
равны нулю.
относительно осиOZ
равны нулю.
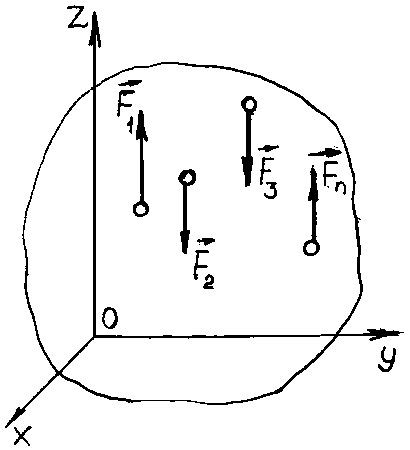
Рис. 4.3. Пространственная система параллельных сил
Значит, уравнения равновесия принимают вид
![]()
![]()
![]() (4.4)
(4.4)
Пространственная система сходящихся сил. Для равновесия тела в случае действия на него пространственной системой сходящихся сил необходимо и достаточно, чтобы суммы проекций всех сил на каждую из осей были равны нулю:
![]()
![]()
![]() (4.5)
(4.5)
![]()
Вопросы для самопроверки
1. Какие уравнения и сколько их можно составить для уравновешенной пространственной системы сходящихся сил?
2. Как определяется момент силы относительно оси?
3. Почему при определении момента силы относительно оси нужно обязательно спроецировать силу на плоскость, перпендикулярную оси?
4. Каким образом нужно расположить ось, чтобы момент данной силы относительно этой оси равнялся нулю?
5. Какие уравнения и сколько их можно составить для уравновешенной пространственной системы параллельных сил?
6. Какие уравнения и сколько их можно составить для уравновешенной произвольной пространственной системы сил?
