
- •Глава 3. Плоская система произвольно расположенных сил (пспрс)
- •3.1. Момент силы относительно точки
- •3.2. Равновесие твёрдых тел под действием пспрс
- •Последовательность действий при решении задач на равновесие плоской системы произвольно расположенных сил
- •3.3. Статически определимые и статически неопределимые задачи
- •План решения задачи на определение реакций опор составной конструкции
- •3.4. Определение усилий в стержнях по способу Риттера
- •Вопросы для самопроверки
- •Примеры
- •Из уравнения (в) получаем:
- •Уравнение проекций сил на ось х имеет вид
- •Полная реакция опоры : ;
- •Или, подсчитав числовые значения, получим:
- •Из уравнения (3.32) реактивный момент:
- •Решение. Составная балка авс находится в равновесии, следовательно, балки ав и вс также находятся в равновесии.
- •Задачи к заданиям
Уравнение проекций сил на ось х имеет вид
![]() ;
;
![]() (3.24)
(3.24)
Силы F и RAY не вошли в уравнение, так как они перпендикулярны оси Х и их проекции на эту ось равны нулю.
Проекции силы на ось Y:
![]() (3.25)
(3.25)
реакция RAX перпендикулярна оси Y, и ее проекция на эту ось равна нулю.
Для составления уравнения моментов за центр моментов принимаем точку А. Плечо силы RB равно длине перпендикуляра, восстановленного из точки А (центра моментов) к линии действия силы RB. Из рис. 3.48, б видно, что AD = (a + b) cos60.
![]() (3.26)
(3.26)
Подставив числовые значения, получим
![]() Н.
Н.
Выразим из (3.25)
![]() .
.
Подставив значения сил, получим
![]() Н.
Н.
Из (3.24)
![]()
Проверим правильность решения задачи, составив уравнения моментов относительно точки В:
![]()
Подставим числовые значения:
![]()
Задача решена верно, так как при подстановке получили тождество 0 = 0.
Полная реакция опоры : ;
![]() Н.
Н.
Ответ:
![]() Н;
Н;![]() Н.
Н.
Пример
85. Для балки
(рис. 3.49, а) определить опорные реакции
по следующим данным:
![]() м,
м, ![]() м,
м,![]() м,
м,![]() кН,
кН,![]() кН,
кН,![]() кН/м,
кН/м,![]() кНм.
кНм.

Рис. 3.49. К примеру 85
Решение. Освободим балку от связей, отбросив опоры и приложив вместо них неизвестные реакции (рис. 3.49, б). Напомним, что для плоской системы параллельных сил достаточно двух уравнений равновесия:
![]() ;
;
![]() .
.
Уравнение моментов относительно точки А
![]() ;
;
(3.27)
![]()
Уравнение моментов относительно точки B
![]() ;
;
(3.28)
![]() .
.
Из уравнения (3.27)

 кН.
кН.
Из уравнения (3.28)

 кН.
кН.
Значение реакции RB получено со знаком «минус». Это означает, что она направлена вертикально вниз.
Для проверки правильности найденных реакций опор балки составляем уравнение
![]() ;
;
![]()
или
![]() .
.
Следовательно, RA и RB определены верно.
Ответ:
![]() кН;
кН;![]() кН.
кН.
Пример 86. Для жестко заделанной консольной балки (рис. 3.50) найти реактивный момент и составляющие реакции заделки.
Принять
![]() кН,
кН,![]() кН/м,
кН/м,![]() кНм,
кНм,![]() м.
м.
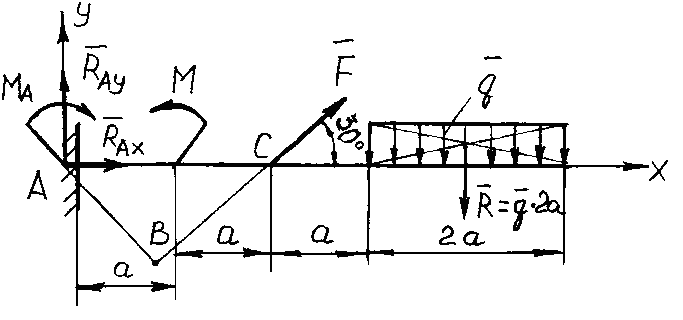
Рис. 3.50. К примеру 86
Решение. Освободим балку от связи, условно отбросив заделку и приложив вместо нее к балке две неизвестные составляющие силы реакции RAX, RAY и реактивный момент MА. Для плоской системы произвольно расположенных сил составим три уравнения равновесия два уравнения проекций и уравнение моментов относительно точки А:
![]() (3.29)
(3.29)
![]() (3.30)
(3.30)
![]() (3.31)
(3.31)
Из уравнения (3.29) получим:
![]() кН.
кН.
Из уравнения (3.30)
![]()
где
![]() кН.
кН.
Тогда
![]() кН.
кН.
Из уравнения (3.31)
![]()
но
![]() м,
м,
тогда
![]() кНм.
кНм.
Проверим правильность решения, составив уравнение моментов относительно точки С:
![]()
Или, подсчитав числовые значения, получим:
![]() ;
;
![]() ;
;
![]() .
.
Задача решена верно.
Значения составляющих RAX и RAY получились со знаком «минус». Это означает, что предварительно выбранное направление оказалось ошибочным. Фактическое направление будет обратным, т. е. составляющая RAX направлена влево, а RAY вниз.
Полная
реакция опоры
![]() :
:
![]() ;
;
![]() кН.
кН.
Ответ:
![]() кН;
кН;![]() кНм.
кНм.
Пример
87. Для балки
(рис. 3.51) определить реакции опоры
защемления в точке А,
если
![]() кН/м,
кН/м,![]() кН и
кН и![]() кНм.
кНм.

Рис. 3.51. К примеру 87
Решение.
Освобождаем балку от связей (заделки)
и заменяем связи силами реакций связей.
В этом случае в точке А
балки возникают силы реакции cвязи
в виде силы RA
и реактивного момента МА.
![]() кН (рис. 3.51, б). Выбираем систему координат
X
и Y
с началом в точке А.
Для решения задачи составляем три
уравнения равновесия:
кН (рис. 3.51, б). Выбираем систему координат
X
и Y
с началом в точке А.
Для решения задачи составляем три
уравнения равновесия:
![]()
![]()
![]()
(Последнее уравнение принимают в качестве проверочного). Уравнения равновесия принимают вид
![]() ;
;
![]() ; (3.32)
; (3.32)
![]() ;
;
![]() ; (3.33)
; (3.33)
![]() ;
;
![]() . (3.34)
. (3.34)
