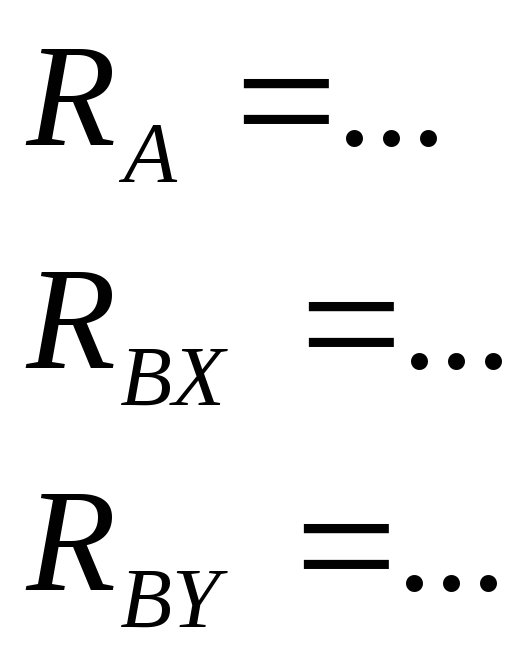Глава 3. Плоская система произвольно расположенных сил (пспрс)

3.1. Момент силы относительно точки

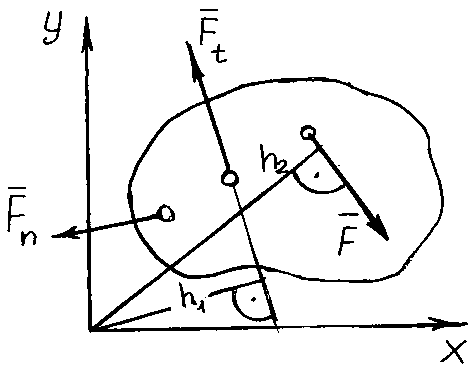
Моментом силы F (рис. 3.1) относительно точки или некоторого центра О называется величина, равная произведению радиуса-вектора , проведенного из данной точки в точку приложения силы, на эту силу:

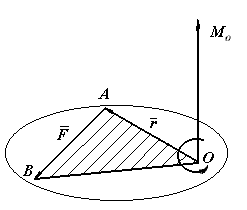
Рис.3.1. Момент силы относительно точки

Момент силы относительно заданной точки является мерой вращательного действия этой силы на тело.

Расстояние от точки О до линии действия силы называется плечом силы и обозначается h.

Если действующие силы находятся в одной плоскости, то моментом силы относительно точки называется произведение модуля силы на плечо, т. е. на длину перпендикуляра, восстановленного из точки, относительно которой берется момент, к линии действия силы. Момент принято считать положительным, если он стремится повернуть тело против часовой стрелки (рис.3.2, а), и отрицательным (рис. 3.2, б), если вращение направлено в противоположную сторону.

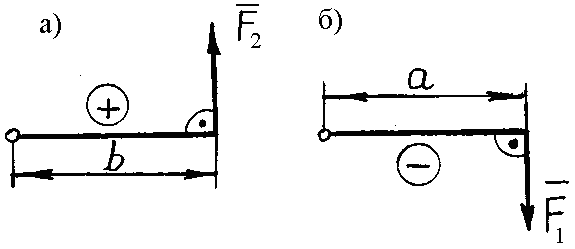
Рис. 3.2. Правило знаков момента силы относительно точки в плоскости действия силы

Необходимо отметить следующее:

- момент силы не изменяется при переносе точки приложения силы вдоль линии ее действия;

- момент силы относительно точки равен нулю только тогда, когда сила равна нулю или когда линия действия силы проходит через эту точку;

- момент силы численно равен площади параллелограмма, построенного на векторах и, или удвоенной площади треугольникаОАВ (см. рис. 3.1).

3.2. Равновесие твёрдых тел под действием пспрс

До сих пор были рассмотрены частные случаи равновесия сил:

а) когда к телу приложены силы, направленные по одной прямой;

б) когда к телу приложено несколько сил, но линии их действия обязательно пересекались в одной точке;

в) когда к телу приложены пары силы.

Рис. 3.3. Произвольная плоская система сил

В реальных условиях тело может находиться в равновесии под действием произвольно расположенной системы сил (рис. 3.3). Условием равновесия является равенство нулю главного момента и главного вектора. На основании этого условия можно составить три уравнения равновесия сил, расположенных в одной плоскости. В зависимости от конкретных условий задачи эти три уравнения могут быть составлены по-разному.

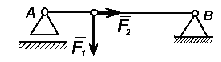
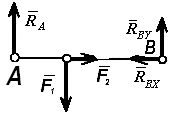
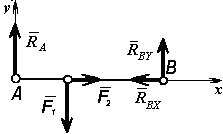
Поясним это следующим примером. На рис. 3.4 показана балка, нагруженная силами F₁, F₂. Требуется определить опорные реакции R_AX, R_AY, R_B.

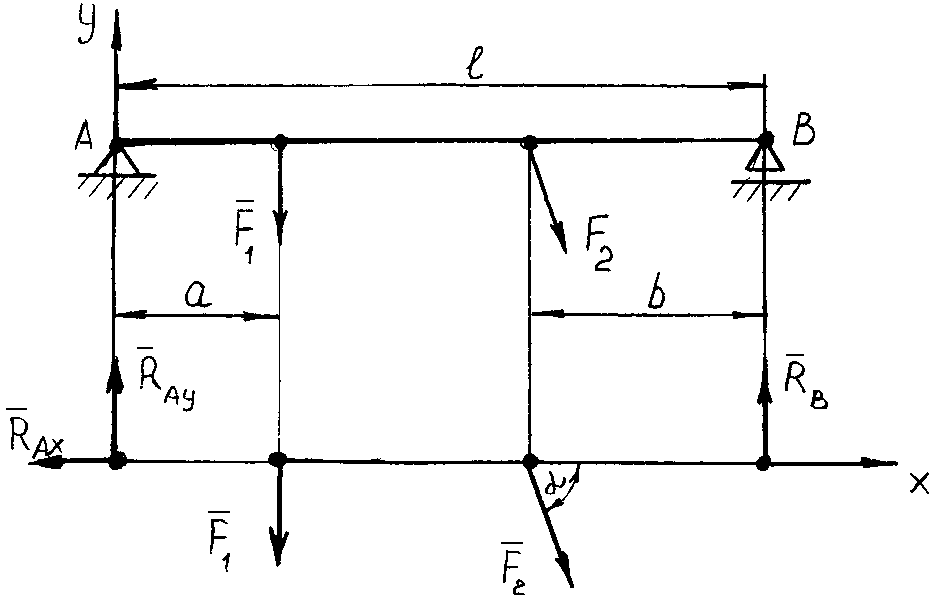
Рис. 3.4. К рассмотрению вопроса об уравнениях равновесия сил

Составим уравнения равновесия:

(3.1)

Уравнения равновесия можно было бы составить следующим образом:

(3.2)

Первый вид уравнений (3.1) более выгодный для решения задач, так как в каждое уравнение входит только одна неизвестная сила, которая может быть определена независимо от других неизвестных сил.

Существует третий вид уравнений (уравнения трёх моментов):

(3.3)

здесь любые три точки А, В, С не должны лежать на одной прямой.

При решении задач на равновесие рекомендуется соблюдать последовательность действий, указанную в табл. 3.1.

Таблица 3.1

Последовательность действий при решении задач на равновесие плоской системы произвольно расположенных сил

Что нужно делать	Иллюстрация действия
1	2
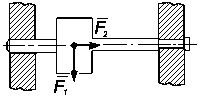
1. Выделить тело (точку), равновесие которого надо рассмотреть

Окончание табл. 3.1

1	2
2. Изобразить расчётную схему, условно изобразить опоры и заданные силы
3. Отбросить опоры (связи), а направление их реакций изобразить на схеме
4. Провести оси координат так, чтобы одна ось была перпендикулярна некоторым неизвестным силам. Наметить центры моментов в точке пересечения линий действия двух неизвестных сил или на линии действия одной неизвестной силы
5. Составить уравнения равновесия объекта исследования
6. Решить уравнения равновесия и определить неизвестные силы
7. Проверить правильность решения задачи по уравнению равновесия, которое не было использовано при решении задачи

Плоская система параллельных сил (рис. 3.5). Пусть линии действия всех сил параллельны оси ОУ. Тогда уравнения равновесия записываются в виде

; (3.4)

или

; , (3.5)

причём точки А и В не должны лежать на прямой, параллельной векторам сил.

Рис. 3.5. Плоская система параллельных сил