Мерзликин Основы теории ядерных реакторов

В соответствии с этой схемой дифференциальное уравнение скорости изменения концентрации самария-149 запишется так:

И, поскольку решение (20.1) неопределённо из-за наличия в нём двух неизвестных функций (NPm(t) и NSm(t)), для того, чтобы замкнуть его, добавляется дифференциальное уравнение для скорости изменения концентрации прометия-149:

Считая в первом приближении, что Ф(t) = idem = Фо, попробуем найти решение этой системы дифференциальных уравнений отравления реактора самарием.

20.2. Потери реактивности при стационарном отравлении реактора самарием

Условиями стационарности отравления реактора самарием-149, очевидно, будут:

NSm(t) = NSmст и NPm(t) = NPmст , или dNSm/dt = 0 = dNPm/dt при Ф(t) = idem = Фо

Поэтому для случаев стационарного отравления дифференциальные уравнения отравления вырождаются в систему линейных алгебраических уравнений:

Складывая почленно эти два уравнения, имеем:

0 = γPm σf5 N5 Фо - σaSm NSmст Фо ,

или после сокращения на ненулевую величину плотности потока нейтронов Фо:

Сразу же отметим принципиальное отличие величины стационарной концентрации самария от стационарной концентрации ксенона: она не зависит от величины

плотности потока нейтронов, а, следовательно, - и от мощности реактора.

Переходя от стационарной концентрации самария к величине потерь реактивности на отравление реактора самарием, имеем:

марием не зависят от мощности реактора, а определяются только величиной коэф-

фициента использования тепловых нейтронов в неотравленном самарием реакторе. Если подставить в (20.2.4) величины физических констант (γPm, σf5 и σа5), то получается:

Представленное на рис.20.2. семейство кривых можно выразить более однозначно, если пересчитать текущие значения отравления в зависимости от энерговыработки реактора (W). В самом деле, поскольку в показателе экспоненты в (20.3.1) стоит величина Фоt, пропорциональная величине энерговыработки реактора W(t) = Npot, такой пересчёт не представляет особой сложности. И если построить зависимость текущего отравления самарием от энерговыработки реактора, то график этой зависимости будет выглядеть так:

ρSmст

Рис.20.3. Нестационарный выход реактора на стационарное отравление самарием в начале кампании.

Таким образом, наиболее значительные изменения потерь реактивности реактора от отравления самарием происходят в первый период кампании.

Реакторы типа ВВЭР-1000 практически выходят на стационарный уровень отравления самарием при энерговыработке W ≈ 28 ÷ 31 тыс. МВт . сут (что составляет около 3.3% от полной расчётной энерговыработки реактора и соответствует около 7 суток работы реактора на номинальной мощности).

При дальнейшей работе реактора слабые изменения отравления реактора самарием имеют место лишь постольку, поскольку в процессе кампании несколько уменьшается величина самого стационарного отравления реактора. Но это происходит плавно и практически незаметно (величина стационарных потерь реактивности от отравления реактора самарием уменьшается на 0.12 ÷ 0.13 % за всю оставшуюся кампанию).

20.4. Нестационарное переотравление реактора самарием после останова («прометиевый провал»)

Тот факт, что при работе реактора в нём накапливается прометий-149, а самарий получается, главным образом, в результате его β-распада, позволяет предсказать, что после останова реактора количество самария в нём должно увеличиваться за счёт β- распада накопленного при работе прометия. А это значит, что отравление реактора самарием после останова реактора должно усиливаться.

Действительно, в момент останова концентрации прометия и самария соответственно равны NPm0 и NSm0, а после останова Фо = 0, и дифференциальные уравнения отравления реактора самарием будут иметь вид:

откуда следует, что в любой момент t после останова сумма производных:

d [N Sm (t) + N Pm (t)] = 0 , а это значит, что NSm(t) + NPm(t) = idem = NSm0 + NPm0 dt

Из последней формулы вытекает, что текущее значение концентрации самария в любой момент времени t после останова реактора будет равно:

Значение текущей концентрации прометия следует из решения уравнения (20.2.2):

NPm(t) = NPm0 exp (- λPm t).

Подставляя его в (20.4.3), получаем выражение для концентрации самария:

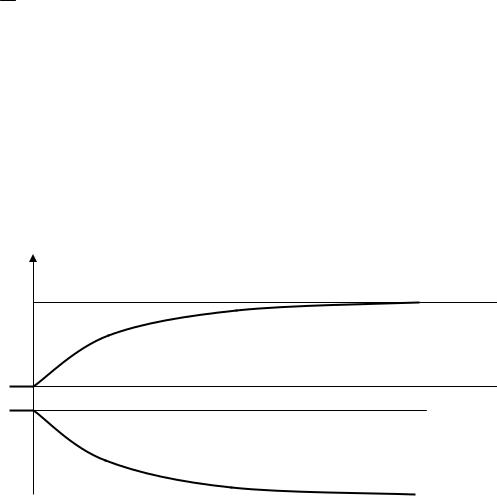
На рис.20.4 показаны переходные процессы изменения концентраций прометия и самария после останова реактора.

N(t)

NSmo+NPmo

NSm(t)

NSmo

NPmo

NPm(t)=NPmo exp(-λPmi)

0 t

Рис.20.3. Убыль концентрации прометия и рост концентрации самария после останова реактора.

Итак, после останова реактора концентрация самария от значения в момент

останова (NSm0) возрастает до значения (NSm0+NPm0) по экспоненциальному закону за счёт β-распада накопленного к моменту останова прометия, и этот рост происходит с периодом, равным периоду полураспада прометия (Т1/2 = 54 часа).

Если перейти от величины текущей концентрации самария к величине текущих потерь реактивности за счёт отравления реактора самарием (по известной формуле), то:

В формуле (20.4.5):

ρSm0 - отравление реактора самарием при останове (чаще всего - стационарное); ρSmпп - максимальное дополнительное отравление реактора самарием, достигаемое

в результате длительной стоянки реактора после останова и обусловленное увеличением концентрации самария сверх значения её в момент останова за счёт распада накопленного до останова прометия.

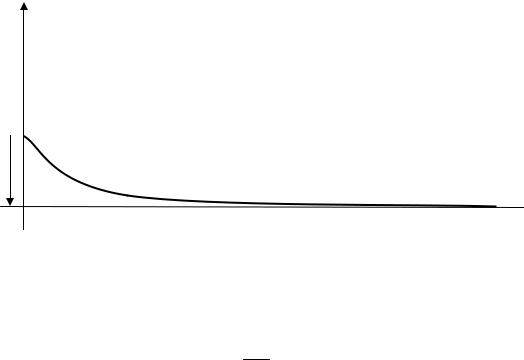
Переотравление реактора самарием после останова принято называть прометиевым провалом (по аналогии с йодной ямой при отравлении реактора ксеноном после останова; «провал», очевидно, потому, что на графике нестационарного переотравления реактора самарием (рис.20.4) переходный процесс действительно формой своей напо-

минает провал с плоским «дном», а «прометиевый», так как, переотравление после останова реактора самарием обусловлено исключительно накопленным до останова прометием). Поскольку эта величина в различных обстоятельствах эксплуатации реактора неодинакова, её зачастую называют глубиной прометиевого провала.

ρSm(t)

0 t

Рис.20.4. Нестационарное переотравление реактора самарием после останова (прометиевый провал).

Глубина прометиевого провала, как несложно сообразить, определяется только концентрацией накопленного к моменту останова реактора прометия, которая

(см.ф.(20.2.2))

N Pmст = γλPm σ 5f N5Фо

Pm

пропорциональна уровню мощности, на котором работал реактор перед остановом.

Чем выше уровень мощности Np0, тем выше величина концентрации прометия в момент останова, тем больше самария будет получено в результате его распада, тем, следовательно, большей будет глубина прометиевого провала.

Время наступления максимума прометиевого провала, в отличие от времени наступления максимума йодных ям, не зависит от режимных параметров реактора, поскольку скорость радиоактивного распада прометия определяется только величиной постоянной распада (или периода полураспада) прометия, который, как известно, равен 54 часам. Ранее неоднократно упоминалось, что практическое время полного распада любого радиоактивного элемента приблизительно равно 6 ÷ 7 периодам его полураспада. Поэтому время наступления максимума прометиевого провала (равное времени практически полного распада прометия) составит:

tпп ≈ 7 Т1/2Pm = 7 . 54 ≈ 380 час ≈ 16 суток.

Следовательно, если реактор простоял после останова более двух недель, - он, как говорят операторы, «находится на дне прометиевого провала».

В связи со сказанным для практика самым, пожалуй, серьёзным является вопрос: сколь велики потери реактивности от нестационарного отравления самарием после останова?

Уже упоминалось, что величина стационарного отравления реактора ВВЭР-1000 самарием лежит в пределах от (- 0.82%) в начале кампании до (- 0.69%) в конце кампании. Глубина прометиевого провала после остановки реактора с номинальной мощности (Npном) составляет (- 0.24%). Казалось бы, по сравнению с глубинами йодных ям, величина самого глубокого прометиевого провала относительно невелика. Однако, уже то, что она составляет приблизительно 0.5 βэ должно заставить эксплуатационника относиться к ней достаточно настороженно и думать, не может ли возникнуть такой практической ситуации, когда эти 0.5βэ скованной самарием реактивности смогут вы-

свободиться при разотравлении (ведь это - большая реактивность). К счастью, такой ситуации как будто не существует, но это не избавляет от необходимости учитывать нестационарное отравление после длительной стоянки реактора в расчётах при последующем пуске его.

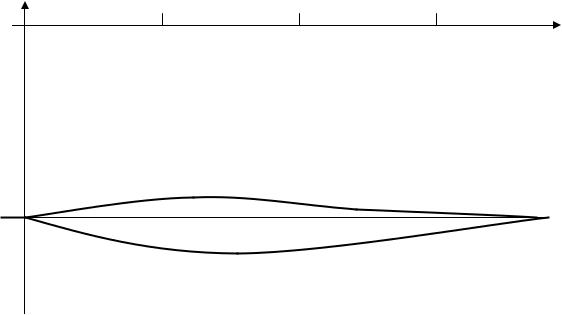
20.5. Переотравление самарием после пуска длительно стоявшего реактора

Попробуем проверить свой уровень понимания самариевого отравления реактора и ответить на вопрос: что будет происходить с величиной отравления реактора самарием, если после длительной (более 15 суток) стоянки реактор пускается вновь и работает на постоянном уровне мощности?

- Поскольку после длительной стоянки уровень отравления реактора самарием выше стационарного (на величину прометиевого провала), а реактор, достаточно длительно работающий на мощности, в конечном счёте должен выйти на стационарный уровень отравления, то при длительной работе реактора на постоянной мощности после долгой стоянки величина отравления самарием должна по прошествии достаточно длительного времени работы реактора снизиться до уровня стационарного отравления, так как весь избыточный самарий (сверх стационарного его количества) за время работы будет расстрелян нейтронами. Реактор должен вернуться к старому уровню стационарного отравления самарием (т.е. к тому, который был в момент последнего останова), так как стационарное отравление не зависит от уровня мощности реактора.

Поэтому нам остаётся ответить лишь на второй закономерно возникающий у эксплуатационника вопрос: каков характер этого переходного процесса ρSm(t) при возвращении реактора «со дна прометиевого провала» к стационарному уровню отравления, и сколько времени будет продолжаться этот переходный процесс?

Ответ на этот вопрос получается из решения системы дифференциальных уравнений отравления реактора самарием при теперь уже не нулевых начальных условиях:

t = 0 NPm = 0 и NSm = NSm0 + NPm0 при Ф(t) = Фо

(чаще всего NSm0 и NPm0 являются стационарными концентрациями 149Sm и 149Pm). Выполнение решения и стандартный переход от текущих концентраций самария к текущим величинам отравления самарием позволяет получить выражение для ρSm(t), графическая иллюстрация которого для различных значений Np приведена на рис.20.5.

rSm(t)

0 Стоянка реактора (³ 15 сут) Пуск Работа на постоянном уровне мощности

t

Рис. 20.5. Переходные процессы изменения отравления реактора самарием при работе реактора на различных уровнях мощности после длительной стоянки.

Из приведенного графика следует, что реактор тем быстрее возвращается к состоянию стационарного отравления самарием, чем выше уровень мощности, на котором он работает после длительной стоянки: при больших плотностях потока нейтронов избыточный (сверх стационарного) самарий расстреливается нейтронами с большими скоростями.

На высоких уровнях мощности(>70÷80%) переходный процесс идёт с «проскоком» уровня стационарного отравления, что объясняется превышением скорости расстрела избыточного самария над скоростью его образования из прометия, который на высоких мощностях в первой половине переходного процесса не успевает накопиться в достаточно большом количестве, чтобы дать скорость распада, близкую к скорости расстрела самария.

20.6. Нестационарное переотравление реактора самарием после перевода реактора на более высокий или более низкий уровень мощности

Казалось бы, вопрос о характере переходного процесса переотравления реактора самарием перед практиком вообще возникать не должен: о каком переотравлении реактора самарием вообще может идти речь, если на протяжении более 90% времени кампании реактор отравлен самарием стационарно, а величина стационарного отравления самарием не зависит от уровня мощности реактора? При этом, казалось бы, после смены уровня мощности реактора его отравление самарием изменяться не должно...

Но дело в том, что динамическое равновесие между образованием и расстрелом самария (свойственное стационарному отравлению) при изменении уровня мощности реактора нарушается: скорость образования самария пропорциональна текущему значению концентрации прометия, а скорость убыли самария пропорциональна текущему значению концентрации самого самария; в итоге получается, что после увеличения мощности реактора (= увеличения Фо) самарий на первом этапе переходного процесса расстреливается интенсивнее, чем образуется, а после уменьшения мощности, наоборот, - в начале переходного процесса расстреливается менее интенсивно, чем образуется (за счёт более высокой в начальный момент концентрации прометия). Потом, когда концентрация прометия увеличивается (или уменьшается, в согласии с увеличением или уменьшением мощности), скорости образования и убыли самария сравниваются, в результате чего текущая концентрация самария достигает минимума (после увеличения мощности) или максимума (после её снижения). На этом первый этап переходного процесса ρSm(t) завершается, и после этого начинается монотонное возвращение концентрации самария к стационарному значению.

Иными словами, графики переходных процессов переотравления реактора самарием после изменения уровня мощности формой своей напоминают графики «холмов» и «йодных ям» переотравления реактора ксеноном, но более сильно растянутые во времени.

После увеличения мощности - переходный процесс ρSm(t) представляет собой плавное отклонение отравления самарием от стационарного значения в сторону уменьшения с последующим плавным возвращением его к стационарному значению.

После уменьшения мощности - процесс переотравления реактора самарием представляет собой плавное отклонение отравления от стационарного значения в сторону увеличения (нечто вроде «прометиевой ямы») с последующим возвращением к исходному стационарному значению отравления.

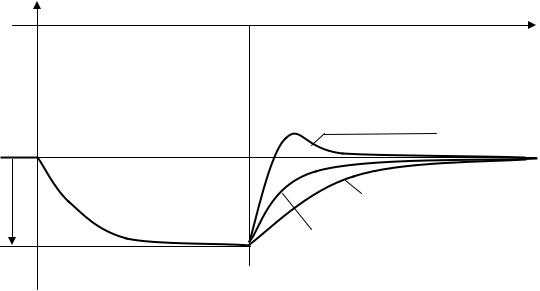
Качественные графики переходных процессов переотравления реактора самарием после изменения уровня мощности реактора показаны на рис.20.6. Рассматривая эти графики, практик должен задаться вопросом: сколь значительны упомянутые экстремальные отклонения от значения стационарного отравления самарием, и сколь долго

продолжаются сами переходные процессы ρSm(t)? Потому что, если они значительны, их надо учитывать и в повседневной практике эксплуатации реактора на них нужно реагировать для поддержания требуемого режима работы реактора.

После повышения уровня мощности

ρSmст

После понижения уровня мощности

Рис. 20.6. Качественный вид переходных процессов переотравления реактора самарием после изменений уровня мощности реактора.

Учитывая тот факт, что упомянутые переходные процессы длятся десятками суток (то есть это очень медленные переходные процессы), а величины отклонений текущих значений самариевых отравлений не очень значительны (не более ± 0.12% по реактивности), причём эти процессы имеют место в периоды эксплуатации, когда реактор работает на постоянном уровне мощности и контроль за плотностью нейтронного потока в реакторе ведётся непрерывно, эти изменения реактивности вследствие переотравлений реактора самарием опасности не представляют и существенного значения не имеют, а потому в практике эксплуатации реакторов АЭС обычно игнорируются.

Раздел 5.

СРЕДСТВА УПРАВЛЕНИЯ РЕАКТОРОМ И ИХ ЭФФЕКТИВНОСТЬ

Тема 21

ЭФФЕКТИВНОСТЬ СТЕРЖНЯ-ПОГЛОТИТЕЛЯ И ГРУППЫ ПОГЛОТИТЕЛЕЙ

21.1. Действие вводимого в активную зону стержня-поглотителя

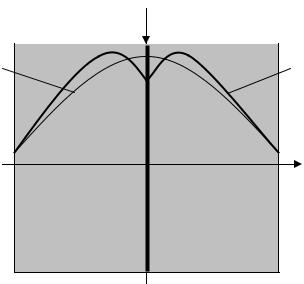
Конечно, введение или извлечение любого стержня поглотителя в активную зону в первую очередь изменяет общие поглощающие свойства активной зоны, что приводит к изменению скорости поглощения нейтронов в реакторе. Но этим дело не исчерпывается. Если вспомнить ранее упоминавшее уравнение баланса тепловых нейтронов

dn/dt = (скорость генерации ТН) – ( скорость поглощения ТН) – ( скорость утечки ТН),

то становится ясно, что, изменяя поглощающие свойства локальной области введения стержня, мы тем самым изменяем не только скорость поглощения тепловых ней-

тронов в этой области, но и распределение плотности потока тепловых нейтронов в

ней и в активной зоне в целом (рис.21.1). Перераспределение плотности потока тепловых нейтронов по объёму активной зоны и топлива приведёт, разумеется, к изменению

скорости реакции деления, а, значит, и скорости генерации нейтронов.

Перераспределение плотности потока тепловых нейтронов в объёме активной зоны приведёт также к изменениям значений плотности потока тепловых нейтронов на границах активной зоны с отражателем, а, следовательно, изменятся и значения градиента плотности потока тепловых нейтронов на границах активной зоны, что приведёт

к изменению скорости утечки тепловых нейтронов из активной зоны. Одним словом,

действие перемещаемого по высоте активной зоны стержня-поглотителя всегда комплексно.

Рис.21.1. Качественный вид перераспределения плотности потока тепловых нейтронов по радиусу активной зоны с введением в неё стержня поглотителя

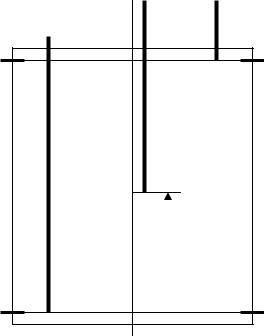
21.2.Характеристика положения стержня-поглотителя в активной зоне

Положение стержня-поглотителя по высоте активной зоны характеризуется от-

стоянием его нижнего конца от плоскости нижнего торца активной зоны. Это от-

стояние принято выражать либо в см, либо в процентах от высоты активной зоны, и обозначать символом Н (рис.21.2).

О стержне, полностью погруженном в активную зону на всю его длину, говорят,

что он находится на нижнем концевом выключателе, имея в виду нижний концевой выключатель (НКВ) электрического привода перемещения стержня, отключающего электродвигатель при достижении стержнем крайнего нижнего положения.

Аналогично о стержне, полностью извлечённом из активной зоны, говорят, что он находится на верхнем концевом выключателе (ВКВ).

Концевые выключатели устанавливаются для того, чтобы ограничить интервал перемещения стержня (или группы стержней) по высоте активной зоны. Чаще всего они устанавливаются даже не точно на верхней и нижней границах активной зоны: как правило, ВКВ устанавливается несколько ниже верхнего торца активной зоны, а НКВ

– несколько выше нижнего торца активной зоны. Это связано с тем, что (как нам предстоит убедиться) вблизи крайних положений подвижные поглотители неэффективны. Поэтому у эксплуатационников принято отсчитывать положение стержня-поглотителя не от низа активной зоны, а от нижнего концевого выключателя.

Иначе говоря, плоскость установки НКВ является нулевой позицией, началом отсчёта для измерения положения любого стержня-поглотителя (или группы поглотителей) по высоте активной зоны.

21.3. Понятия об интегральной и дифференциальной эффективности

Интегральной эффективностью подвижного поглотителя в рассматриваемом его положении по высоте активной зоны (Н) называется величина положительной реактивности, сообщаемой реактору при подъёме этого поглотителя от НКВ до этого положения Н.

Величина интегральной эффективности поглотителя обозначается ρ(Н) и в соответствии с определением измеряется в единицах реактивности ( в а.е.р., % или долях