Мерзликин Основы теории ядерных реакторов

Тема 19

ОТРАВЛЕНИЕ РЕАКТОРА КСЕНОНОМ

Отравление реактора - это процесс накопления в нём короткоживущих продуктов деления, участвующих в непроизводительном захвате нейтронов и тем самым снижающих запас реактивности реактора при их образовании и, наоборот, высвобождающих его при их β-распаде.

Особенностями процесса отравления по сравнению с другими ранее рассмотренными процессами, приводящими к потерям запаса реактивности, является то, что:

*Процесс отравления, как принято предполагать, вызывается накоплением только одного β-активного продукта деления - ксенона-135, - который характеризуется ве-

личиной стандартного микросечения поглощения σa0Xe = 2720000 барн, величинами удельного выхода γXe = 0.003 и периода полураспада Т1/2Xe = 9.2 часа (или величиной постоянной β-распада λXe = 2.09 . 10 -5 c-1).

*Отравление - протекает существенно быстрее, чем процессы выгорания, шлакования и воспроизводства. Переходные процессы отравления и переотравлений реактора ксеноном длятся не более трёх суток.

*В отличие от указанных выше процессов, отравление - процесс обратимый: при возрастании концентрации ксенона-135 реактор отравляется (и теряет запас реактивности), при снижении концентрации ксенона - он разотравляется (что приводит к высвобождению положительной реактивности).

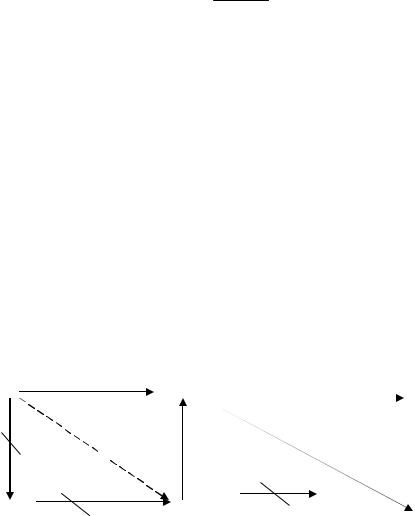
*Если посмотреть на совмещённый график энергетических спектров для теплового, промежуточного и быстрого реакторов вместе с зависимостью сечения поглощения 135Xe от энергии нейтронов Е (рис.19.1), то станет ясно, что отравление ксеноном существенно для тепловых реакторов, малосущественно - для промежуточных и несущественно - для быстрых реакторов.

Т

n(E)

σaXe(E)

П

Б

0

E

Рис.19.1. Различия в поглощении нейтронов ксеноном-135 в тепловом (Т), быстром (Б) и промежуточном (П) реакторах.

Количественными мерами отравления реактора ксеноном, подобно мерам оценки рассмотренных ранее процессов, являются:

∙ относительная доля поглощаемых ксеноном нейтронов, равная отношению скоростей поглощения тепловых нейтронов ядрами ксенона и ядрами 235U:

* потери реактивности от отравления ксеноном, связанные с величиной доли поглощения нейтронов ксеноном (в любой момент времени) зависимостью:

где θ - коэффициент использования тепловых нейтронов в неотравленном реакторе.

19.1. Схема образования и убыли 135Xe и дифференциальные уравнения отравления реактора ксеноном

135Xe образуется в реакторе двумя путями: непосредственно как осколок деления 235U с известным удельным выходом (γХе = 0.003) и как дочерний продукт b-распада йода-135, который сам является продуктом b-распада теллура-135, образующегося при делении с довольно большим удельным выходом (γТе = 0.06). Исчезает 135Xe также двумя путями: в результате поглощения тепловых нейтронов (иначе: за счёт его расстрела тепловыми нейтронами или выгорания) и в результате его b-распада. При поглощении ядром 135Xe на его месте образуется шлак третьей группы - 136Xe с микросечением поглощения тепловых нейтронов σа » 5 барн. При b-распаде 135Xe образуется также слабый шлак третьей группы - 135Cs - с микросечением поглощения σа » 6 барн.

Схематически наиболее важные процессы, приводящие к изменениям количества накапливаемого ксенона-135, выглядят так:

Рис.19.2. Схема образования и убыли йода и ксенона и её упрощение.

Штриховыми линиями на схеме выделены некоторые коррекции её, к которым обычно прибегают для упрощения описания процессов отравления реактора. Суть первого упрощающего допущения состоит в том, что, поскольку период полураспада тел- лура-135 во много раз меньше периода полураспада йода-135, можно приближенно считать, что йод-135 является непосредственным осколком реакции деления с фиктивным удельным выходом, равным величине истинного удельного выхода теллура-135. (В самом деле, если период полураспада теллура столь мал, что он распадается практически сразу после своего образования, то без особого ущерба для точности можно счи-

тать, что непосредственным продуктом реакции деления является не теллур, а его дочерний продукт - йод-135).

Второе упрощение состоит в том, что из-за малости микросечения поглощения йода-135 убылью его вследствие поглощения обычно пренебрегают.

На основании такой упрощённой схемы дифференциальное уравнение скорости изменения концентрации 135Xe запишется как разность двух скоростей прибыли и двух

скоростей убыли его:

Скорости прибыли Xe Скорости убыли Xe

Полученное уравнение содержит две неизвестных функции (Nxe и NJ), а потому для получения однозначного решения оно должно быть дополнено ещё одним уравнением с независимо фигурирующей в нём концентрацией NJ(t). Скорость изменения концентрации 135J является разницей скоростей образования 135J (как непосредственного продукта деления) и убыли его (за счёт β-распада):

Полученная система двух дифференциальных уравнений (19.1.1)÷(19.1.2) называ-

ется системой дифференциальных уравнений отравления реактора ксеноном.

19.2.Стационарное отравление реактора ксеноном.

19.2.1. Суть стационарного отравления реактора ксеноном. В первоначаль-

ный момент работы на мощности реактор, как правило, разотравлен, то есть концентрации йода и ксенона в его твэлах - нулевые. Но при работе реактора концентрации того и другого начинают расти, и несложно представить себе, до какого уровня они будут расти. Поскольку скорость убыли ксенона прямо пропорциональна величине его концентрации (взгляните на последние два слагаемых (19.1.1)), то какой бы ни был характер его образования, рано или поздно количество накопленного ксенона достигнет такой величины, что скорость его убыли сравняется со скоростью его образования. В этом случае концентрация накопленного ксенона должна стабилизироваться по величине (то есть достигнуть стационарного значения). И очевидно, что для достижения этого состояния реактор должен работать на постоянном уровне мощности и проработать на этом уровне мощности достаточно длительное время. Какое именно - увидим далее.

Стационарным называется отравление, свойственное реактору, длительно работающему на постоянном уровне мощности, в результате чего в его твэлах устанавливаются постоянные во времени концентрации йода и ксенона.

Таким образом, условиями стационарности отравления реактора 135Хе являются:

причём, последние два условия равносильны условиям:

19.2.2. Величина стационарного отравления ксеноном. Если подставить усло-

вия (19.2.1) и (19.2.2) в дифференциальные уравнения отравления реактора (19.1.1)- (19.1.2), последние перестают быть дифференциальными, становясь обычными алгебраическими линейными уравнениями:

Из уравнения (19.2.4) находится величина стационарной концентрации 135I:

Отметим на будущее: величина стационарной концентрации йода-135 прямо про-

порциональна величине уровня мощности, на котором работает реактор (так как ве-

личина концентрации 235U в течение нескольких суток работы реактора на постоянной мощности уменьшается незначительно, величина мощности реактора оказывается пропорциональной величине плотности потока нейтронов в твэлах реактора Фо).

Величину стационарной концентрации ксенона проще всего найти, если почленно сложить уравнения (19.2.3) и (19.2.4):

И, следовательно, величина потерь реактивности при стационарном отравлении реактора ксеноном (в соответствии с формулой (19.2)):

Следовательно, потери запаса реактивности при стационарном отравлении реактора ксеноном определяются:

а) Величиной концентрации урана-235 (или величиной обогащения топлива) - в

той мере, в какой эта величина определяет величину коэффициента использования тепловых нейтронов θ : чем больше концентрация N5 - тем больше величина θ - и тем, следовательно, больше будет абсолютная величина потерь реактивности при стационарном отравлении ρXeст.

б) Величиной уровня мощности, на котором длительно работает реактор Np0 (которая в течение относительно непродолжительного времени отравления прямо пропорциональна величине плотности потока тепловых нейтронов в топливе реактора Фо). Эта зависимость отравления реактора от его мощности настолько важна для эксплуатационника, что есть смысл остановиться на ней подробнее.

19.2.3. Зависимость стационарного отравления ксеноном от мощности реак-

тора. Если подставить в формулу (19.2.7) значения всех известных физических кон-

Небольшой расчёт по этой формуле позволяет убедиться, что:

при Фо < 1011 нейтр/см2с (такие плотности потока свойственны реактору, работающему на МКУМ) отравление реактора практически отсутствует (ρXeст » 0);

при Фо > 5 . 1014 нейтр/cм2с (а такие величины Ф свойственны только импульсным экспериментальным реакторам) величина стационарного отравления практически

достигает своего теоретического предела (ρXeст)пред » - 0.054 q = - 5.4 q %.

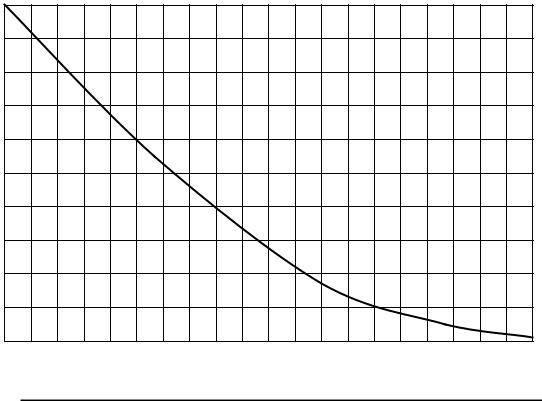
В интервале промежуточных значений Фо (1011¸1014 нейтр/см2с) - свойственных энергетическим реакторам АЭС - зависимость величины стационарного отравления от величины плотности потока нейтронов в твэлах реактора имеет нелинейно возрастающий характер, причём, по мере роста величины плотности потока нейтронов темп роста стационарного отравления реактора ксеноном монотонно падает до нуля (при приближении к величине теоретического предела отравления).

-ρХест /θ 0.06

Теоретический предел величины стационарного отравления реакторов

0.054

0.04

0.02

Рис.19.3. Качественный вид зависимости величины стационарного отравления реакторов ксеноном от величины средней плотности потока тепловых нейтронов в топливе твэлов.

Эксплуатационника в большей степени интересует не эта зависимость, имеющая, скорее, академический характер, а практическое приложение её к конкретному реактору, которым он управляет.

Но вы, конечно, понимаете, что в любом конкретном реакторе каждому значению мощности реактора соответствует своё значение средней плотности потока тепловых нейтронов, и в любой момент кампании это соответствие - однозначное. А это значит, что участок теоретической кривой, показанной на рис.19.3, можно пересчитать (и перестроить) в график зависимости стационарного отравления конкретного реактора от его

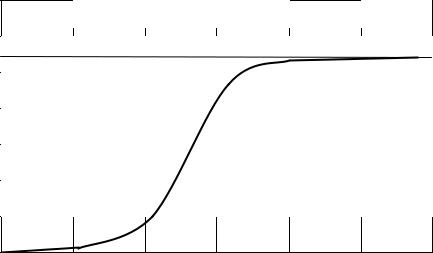
уровней мощности (рис.19.4). Этот график эксплуатационники кратко называют кривой стационарных отравлений. Обычно он строится в натуральном масштабе, то есть величина мощности реактора выражается либо абсолютно (в МВт), либо в относитель-

ных единицах (чаще всего в процентах от номинальной мощности реактора).

Кривая стационарных отравлений, построенная в удобном масштабе, позволяет быстро оценивать величину потерь реактивности реактора вследствие стационарного отравления ксеноном на любом уровне мощности.

- 1

- 2

ρХест, %

Рис.19.4. Типичный качественный вид кривой стационарных отравлений реактора.

19.2.4. Характер роста потерь запаса реактивности из-за отравления 135Xe первоначально разотравленного реактора в первый период работы на постоянном уровне мощности. Если реактор запускается после достаточно длительной стоянки и работает на постоянном уровне мощности, то величина потерь реактивности с момента начала работы на мощности от нуля через некоторый отрезок времени в соответствии со всем сказанным ранее должна достигнуть стационарного уровня. Практика должны заинтересовать, по крайней мере, два вопроса: каков характер роста потерь реактивности до достижения уровня стационарного отравления и за какое время работающий на постоянном уровне мощности реактор достигает стационарного отравления?

Характер роста потерь реактивности при выходе реактора на стационарное отравление выясняется из решения системы дифференциальных уравнений отравления реактора при нулевых начальных условиях и условии Ф(t) = idem = Фо. Решение уравнений и переход от концентраций Nxe(t) к потерям реактивности за счёт отравления ксеноном даёт следующее выражение для переходного процесса rXe(t):

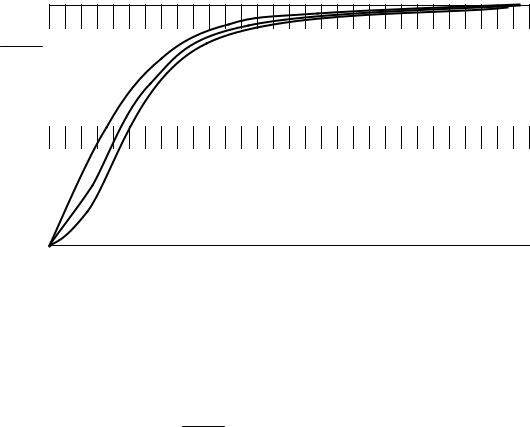
Формула (19.2.8), если мысленно подставить в неё все нейтронно-физические константы, обретает существенно более простой вид, который подсказывает, что текущие величины отравлений реактора ксеноном не линейно зависят от уровня мощности реактора (или Фо). Расчёт по этой формуле для различных величин Фо (в том числе и для Фо = ¥)) качественно иллюстрируется графиком, представленным на рис.19.5. Из него следует, что при малых значениях плотности потока тепловых нейтронов (или на малых уровнях мощности реактора) переходный процесс ρXe(t) протекает в несколько более замедленном темпе, чем при больших значениях Фо (на больших уровнях мощности). Предельный случай этих переходных процессов (при Фо ® ¥) вырождается в одну экспоненту:

поскольку при Фо® ¥ первая из экспонент формулы (19.2.8) обращается в нуль, а коэффициент перед второй экспонентой - в единицу

1.0

ρXe (t)

ρXeст

0.5

Рис.19.5. Переходные процессы нестационарного выхода первоначально разотравленного реактора на стационарный уровень отравления. Нижняя кривая соответствует Фо = 20% Фоном, средняя кривая – 100% Фоном, верхняя – Фо = ∞.

Факт не очень существенной зависимости переходных процессов ρXe(t) от плотности потока нейтронов (практически - от мощности реактора) даёт возможность с достаточной для практических целей точностью приближенно оценивать величины текущих значений отравления реактора ксеноном по формуле (19.2.9):

ρXe (t) » 1 - exp(-λ t) ,

ρXeст J

справедливой, строго говоря, только для идеального случая бесконечно больших мощностей реактора.

19.2.5. Время наступления стационарного отравления реактора. Экспонента,

какая бы сложная она ни была, - кривая асимптотическая: она достигает своего устано-

вившегося (стационарного) значения лишь по прошествии бесконечного по величине отрезка времени. Практически (то есть с относительной погрешностью не более 1%) текущее значение экспоненты сравнивается с её стационарным значением за время, равное 6 ÷7 периодам её «уполовинивания», то есть в данном случае – 6 ÷7 периодам полураспада, определяющего переходный процесс изменения концентрации йода-135. А так как период полураспада йода-135 известен (Т1/2 = 6.7 часа), то время практического наступления стационарного отравления реактора ксеноном:

И оказывается практически неважным, на каком уровне мощности работал реактор эти двое суток, так как после 47 часов все экспоненты практически сливаются в одну. Итак, запомним:

Время практического наступления стационарного отравления реактора, работающего на любом неизменном уровне мощности, составляет двое суток.

После этого, если реактор продолжает работать на этом же уровне мощности, величина отравления реактора ксеноном не изменяется. А это значит, что оператору после наступления стационарного отравления не придётся предпринимать действий по компенсации изменений реактивности реактора, необходимых для удержания реактора в критическом состоянии на заданной мощности.

19.3.Переотравление после останова реактора («йодная яма»)

Вопрос о том, как меняется текущее значение потерь реактивности реактора (которое мы, невольно перейдя на профессиональный жаргон операторов АЭС, кратко называем отравлением реактора) волнует оператора потому, что после вынужденного останова реактора (связанного, как правило, с необходимостью ликвидации неполадок) реактор необходимо снова пускать, и от того, какую величину потерь реактивности потребуется компенсировать при пуске, зависят те конкретные действия, которые должен предпринимать оператор реакторной установки.

Временная функция текущих потерь реактивности за счёт отравления ксеноном после останова реактора находится путём решения дифференциальных уравнений отравления, но уже не при нулевых начальных условиях, а при таких: при t = 0 Ф(t) = 0, Nxe = Nxeст и NJ = NJст (подразумевая под этим, что к моменту останова реактор проработал на постоянном уровне мощности более 3 суток, а потому он - стационарно отравлен на этом уровне мощности). А можно закономерность отравления реактора после останова проследить, не прибегая к решению системы дифференциальных уравнений, из достаточно простых рассуждений.

19.3.1. О соотношении скоростей β-распада 135I и 135Xe в реакторе. Для начала отметим, что λJ = 2.87 . 10 –5 c-1 > λXe = 2.1 . 10 –5 c-1, то есть при равных концентрациях йод распадается с большей скоростью, чем ксенон. Тем более скорость распада йода будет больше скорости распада ксенона, если NJ > NXe, что и имеет место в момент останова стационарно отравленного реактора, что мы и собираемся показать. Так как стационарная концентрация йода (см.(19.2.5))

NJст/NXeст ≈ 0.6897 + 8.93 . 10 -14 Фо.

Последнее равенство означает, что соотношение стационарных концентраций йода и ксенона с увеличением уровня мощности реактора растёт по линейному закону от величины мощности Nр.

Решив простое линейное уравнение, нетрудно увидеть, что уже при значениях плотности потока тепловых нейтронов в твэлах реактора Фо > 3.4.1011 нейтр/см2с (что соответствует МКУМ реакторов типа ВВЭР) величина этого соотношения становится выше единицы, то есть при любых реальных уровнях мощности реактора стационарная

концентрация йода выше стационарной концентрации ксенона (NJст > NXeст).

в любой момент времени работы стационарно отравленного ксеноном реактора, в том числе и в момент его останова. Физически это означает, что величина скорости

радиоактивного распада йода на любых реальных уровнях мощности реактора всегда выше скорости радиоактивного распада ксенона.

Это замечание помогает легко понять, почему в начальный период после останова реактора концентрация ксенона растёт, то есть реактор продолжает отравляться.

19.3.2. Механизм образования «йодной ямы» после останова. С момента ос-

танова реактора величина Фо = 0, и дифференциальные уравнения отравления реактора приобретают более простой вид:

Решение второго из них имеет вид хорошо знакомой нам экспоненты закона радиоактивного распада:

N J (t) = N Jo exp(-λJ t) .

Что касается уравнения (19.3.2), то и, не решая его, можно увидеть, что, поскольку правая его часть в момент останова положительна (в силу (19.3.1)), то и левая его часть - тоже положительна, то есть dNXe/dt > 0.

Положительный знак производной означает, что с момента останова реактора функция Nxe(t) - возрастающая, поскольку скорость образования ксенона из распадающегося йода превышает скорость его распада.

Но по мере распада накопленного до останова йода скорость его распада падает (концентрация снижается по экспоненциальному закону), а это значит, что и величина λJNJ(t) - λXeNXe(t) = dNXe/dt - тоже падает со временем. И это падение будет продолжаться, очевидно, до тех пор, пока уменьшающаяся скорость распада йода не сравняется со скоростью распада ксенона. В этот момент t* величина первой производной dNXe/dt станет равной нулю, а это значит, что величина концентрации ксенона Nxe(t*) в этот момент достигнет максимума, после чего производная dNXe/dt станет отрицательной, а сама функция Nxe(t) - убывающей функцией.

И это несложно понять: поскольку, начиная с этого момента t* нераспавшегося йода осталось настолько мало, что скорость образования ксенона из распадающегося йода становится меньше скорости распада ксенона, то текущее значение концентрации ксенона после момента t* будет падать. И это падение будет продолжаться до тех пор, пока не распадутся весь накопленный в реакторе йод и весь накопленный и полученный из йода ксенон.

NXe(t)

NXeo

t

0 t*

Рис.19.6. Качественная картина изменений концентраций йода и ксенона после останова реактора.

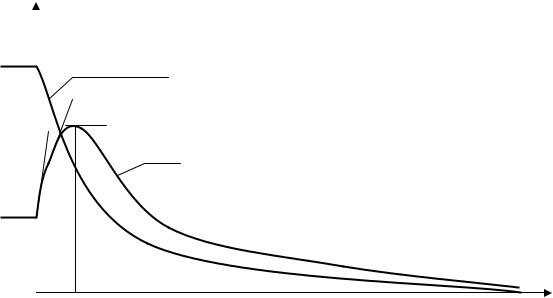
Переходя от текущей концентрации ксенона Nxe(t) к потерям реактивности за счёт отравления реактора ксеноном по известной зависимости (19.2), можно пересчитать и перестроить график рис.19.6 в график зависимости ρXe(t) после останова реактора (по существу повторяющем график Nxe(t) в «зеркальном отражении» в другом масштабе).

Формой этот график действительно напоминает яму (рис.19.7), и, хотя речь идёт об отравлении реактора не йодом, а ксеноном, переходный процесс изменения во времени потерь реактивности за счёт отравления ксеноном после остановки реактора получил краткое название йодной ямы. Йодной, очевидно, потому, что образующийся после останова ксенон получается в результате распада накопленного до останова йода.

Йодная яма - это нестационарное переотравление реактора ксеноном сверх

отравления его на момент останова, обусловленное превышением темпа распада йода, накопленного до момента останова, над темпом распада ксенона.