19. Построение первого опорного плана транспортной задачи по методу северо-западного угла.

Вначале полагают все переменные равными 0, при этом клетки таблицы условий считаются свободными. После того, как определено значение какой-либо переменной , оно заносится в соответствующую клетку , которая теперь будет называться занятой.

Рассматриваемые методы построения первого опорного плана гаран­тируют получение в исходном плане занятых клеток. Это озна­чает, что опорный план является невырожденным.

Алгоритм метода северо-западного угла

Заполнение клеток таблицы условий начинается с левой верхней клетки для неизвестного .

Шаг 1. Выбранной переменной присваивают значение , где и – текущие значения запаса и спроса.

Шаг 2. Если , то исключают из дальнейшего рассмотрения -ю строку и устанавливают текущее значение равным .

Переходят к шагу 5.

Шаг 3. Если , то исключают из дальнейшего рассмотрения -й столбец и текущее значение определяют как .

Переходят к шагу 5.

Шаг 4. Если , то исключают из дальнейшего рассмотрения сначала -ю строку (или -й столбец). Затем в -м столбце (или -й строке) выбирают одну из переменных, не исключенных ранее, полагают ее равной 0, и также исключают соответствующий (-ую) стол­бец (строку).

Переходят к шагу 5.

Шаг 5. Если присвоены значения менее чем переменным, выбирают не исключенную переменную «северо-западного» угла и возвращаются к шагу 1. Если определены значения переменных, алгоритм закончен.

20. Построение первого опорного плана транспортной задачи методом минимального элемента.

Сущность способа в том, что на каждом шаге заполняется та клетка оставшейся части таблицы, которая имеет наименьший тариф; в случае наличия нескольких таких равных тарифов заполняется любая из них. В остальном действуют аналогично предыдущему способу.

21.Определение оптимального плана транспортной задачи методом потенциалов

2 Метод min тарифа (таблица в тетради)

F(x)=2*120+0*80+1*180+7*90+0*0+2*130=1310 т.е. почти на половину меньше затрат

Нахождение оптимального плана ,методом потенциала

3)Для загруженных клеток находим уравнение для определение потенциалов строк

() и столбцов ()

()+ ()= (*)

Т.к. число потенциалов (m+n),а число загруженных клеток S=m+n-1,то 1 потенциал принимает произвольно (=0) ,а ост. Находим из соответствия (*)

Находим последовательно потенциалы используя соотношения:

=-,если изв.

=-,если известно

4)Для свободных клеток составляем -оценки.

= + - (**)

Если все ,то план оптимальный ,решение закончено

Если ,то план оптимальный и единственный.

=0+1-4=3

=0+7-11=-4

=0+2-5=-3

=-5+2-3=-6

=-5+1-6=-10

=-5

План оптимальный и единственный ,т.к.

Затраты:

F(x*)=1310

Ответ :

Из 1 склада –из А1 отправляем в В1 =120 ед.груза и 80 ед. ост.на складе А1.Из А2 направляем в В2 =180 ед.груза и в В3 =90 ед.груза. Из А3 направляют в В3 ед.груза. Суммарные затраты составляют F(x*)=1310 (ед.)

Алгоритм –метод минимального элемента(тарифа)

1 шаг. Составление таблицы ТЗ

4.ЦФ-время ,тогда тарифы –время перевозки ,которое минимизируется (скоропор.продукты ,в основ.действия)

5.Целочисленность .Доказано ,что если ТЗ все параметры целые числа ,то и решение тоже будет целочисленно .

22.Задача о назначениях. Математическая модель и метод ее решения

Модели этих задач мы получим ,решая дом.задания (1.5 ;1.6 ;1.11 –задание 4 и 5)

О назначениях:

Задача 1.

Работодатель нанимает группу служащих .Как распр-ть их по работам ,чтобы обеспечить суммарную эффективность производительности труда (),чтобы максимизировать суммарную эффективность всех работников.

Решение :

1)Цель- максимизировать суммарную эффективность работников

2)Параметры :

m-(число работников)

n-(число рабочих мест)

-(производительность того работника на той работе)

=1 (i=1,m)

=1 (j=1,n)

3) Упр.переменные :

(см.далее формулу 3.4.)

4)Кр.эффект-ти:

F(x)= + max (1)

5)ОДР

= (2)

=1 i=1,m (3)

=1 j=1,n (4)

Особенности задачи :

1,если работник занял должность

0,если работник не занял должность

Задача решается распределительным методом

Задача 2

Решить задачу 2 ,если ,то трудоемкость i-ой работы j-тым работником.

В отличие от матем.модели задача 2:

1)Цель –минимизировать общую трудоемкость всех работ

4)ЦФ:

F(x) min

Задача решается распределительным методом

1.План минимального тарифа.

23.Задача дробно-линейного программирования. Сведение задачи дробно-линейного программирования к задаче линейного программирования

Дробно-линейное программирование (ДЛП) – математическая дисциплина, посвящённая теории и методам решения задач об экстремумах отношений линейных функций на множествах N-мерного векторного пространства, задаваемых системами линейных уравнений и неравенств.

Рассмотрим алгоритм решения, основанный на сведении ЗДЛП к ЗЛП на примере максимизации рентабельности продукции.

1). Цель: максимизация рентабельности продукции

2). Параметры:

– цена и переменные затраты на производство продукции;

С – постоянные затраты;

- расход i-того ресурса на производство j-той продукции

i =

j =

– запас j-того ресурса.

3). Переменные: - искомое количество единиц j-той продукции.

4). Пусть ЦФ – рентабельность продукции, то есть отношение прибыли от реализации к общему объёму затрат.

Здесь - маржинальная прибыль от реализации j-той продукции.

5). ОДР:

(2)

(3)

Таким образом, имеем (1), (2), (3) – ЗДЛП.

Сведём задачу (1), (2), (3) к линейной. Обозначим знаменатель через V.

Ограничения разделим на V и введём новые переменные.

Получаем ЗЛП:

(7)

(8)

ЗЛП (6), (7), (8) имеет смешанный вид.

В последнее уравнение (7) вводим искусственную переменную , и на ЦФ (6) накладываем штраф .

Решаем ЗЛП методом искусственного базиса и получаем оптимальное решение:

Тогда искомое оптимальное решение находится по формулам:

Так как:

Значение максимальной рентабельности находится по формуле (1).

24.Модель распределительной задачи. Сведение математической модели распределительной задачи к математической модели транспортной задачи.

Это задачи распределения ресурсов по работам.

Рассмотрим классическую задачу

Распределение времени работы взаимозам. оборудование по производству изделий.

1)Постановка задачи

m-число типов станков

n-количество видов продукции

-время работы станка ()по производству пр.( )часы

t0-фонд рабочего времени станка ()

-обьем производства ()шт

-производительность ()по производству ()

–ссебестоимость работы 1-го станко-часа () по производству ()

Задача :

При заданных пар-х найти время t ,при котором суммарно достаточно по производству продукции минимальны.

2)Мат.модель РЗ

(1)F(x)= min

(2) (по строкам )

(3) * = (по столбцам)

(4)

4)Алгоритм решения

1.Выбираем станок (э),у которой средняя мощность мах

2. = ,=1

3. (=

4. =

5.Тарифы

6.Решаем ТЗ с переменными.

ТЗ (, и ) {}

7.Искомое время.

*=

8.Минимальные затраты (по ф.(1))

F(t*)= ;*(,*)

Таким образом решение РЗ на основано на сведении от к соответс-ей ТЗ.

25.Задачи целочисленного программирования. Метод Гомори

Экстремальная задача ,переменные которой принимают целочисленного решения ,наз.заданий целочисленного программирования(ЗЦП)

Алгоритм Гомори ,которое используется для решения полностью целочисленных задач линейного программирования. Он вкл. этапы:

1.Решается ЗЛП без учета целочисленности .Если ЗЛП не разрешима ,то и ЗЦЛП не разрешима .Если оптимальное решение переменных –целое ,то решение закончено .

Иначе,

2.Среди дробных чисел выбирается элемент с наибольшей дробной частью и сост-ся дополнительное ограничение (пусть это i-ое ограничение)

– (*)

Здесь :

, -дробные части свободного члена и коэф-тов i-того ограничения(сечение Гомори)

Замечание :

Целая часть числа [a]-это наибольшее число ,не превосходящее число а, а дробная часть числа –разность между числом и его дробной частью .

Например :

{}=

{-}=

Таким образом ,дробная часть числа всегда неотрицательна.

Неравенство преоб-ся в уравнение путем введения дополнительной неотрицательной переменной

3.Полученная расшир.задача решается с-методом (можно использовать двойств. с-метод )

Если оптимальные решения целые ,решение закончено .Иначе переходят к шагу 2.

Пример :

У фермера доля приобретения оборудования по сортировке сырья имеется в наличие 34 д.е..Оно может быть размещено на площади не >.Фермер может заказать оборудование:

1)Вида А стоимостью 3 д.е. ,на площади по,с производительностью 2 тонны/сутки.

2)Вида В стоимостью 4 д.е.(за шт)на площади по и с производительностью 3 тонны/сутки.

Требуется составить оптимальный план покупки оборудований ,обеспеч-щий мах общую производительность при условии ,что фермер не может купить >8 машин типа В

Решение :

1.Решаем ЗЛП

Переменные :х1 и х2 –количество машин типа А и В соответственно.

Цель :максимизация общей производительности F(x)

Тогда имеем ЗЛП в стандартном виде:

F(x)=2*x1+3*x2 max (1)

3*x1+5*x2 60

3*x1+4*x2 34 (2)

х2 8

х1 и х2>0 -целые (3)

Оптимальное решение (3-я с-таблица) х*=( ;8; 18; 0; 0)

2.Т.к. оптимальное решение не целочисленно ,то сост-ся дополнительное ограничение

Таблица с баз,баз. 0,2,3,0,0,0,Q и т.д.

Составляем дополнительное ограничение (сечение Гомори)для 2-ой строки и 3 –ей с-таблицы по ф.(*)

В дробной части :

{} - }*

{} = = , =

--

Водим дополнительную неотрицательную переменную х6.Получаем ур.отсечений.

-** -* +

Это уравнение записываем в ограничение таблицы 3(сечения Гомори)

В базис вводим переменную с наименьшим по модулю значением ср.оценки ,опред-ой как отношение -оценок к дробным элементам строки Гомори .:

(<2)- поэтому вводим в базис вместо. Ключевой элемент = -. .Делим эту строку на (-) ,ост.находим по пр. прямоугольника.

В 4-ой с –таблице все значения переменных –целые

Получено оптимальное целочислительное решение.

Х*=(2;7;19;0;1;0)

Решение:

Приобретаем 2 машины типа А и 7 машин типа В, незанятая площадь составляет 19,остаток денег 0,резерв до лимита машин В -1 машина

Суммарная производительность равна:

2*2+3*7=25(т/сутки)

26. Общая постановка векторной задачи математического программирования (ВЗМП). Примеры многокритериальных задач принятия решений.

В формальной модели ЗПР:

В условиях проблемной ситуации Sо, времени T и ресурсов Q,необходимо построить модель ситуации S, сформировать множество целей А, ограничений В и альтернативных вариантов решения Y, произвести оценку индивидуальных предпочтений Р и найти оптимальное решение Yопт, руководствуясь по критерию выбора k на основе принципа согласования L.

В формальной модели ЗПР для оптимального решения Yопт рассмотрим параметр ЗПР-принцип согласования L.

Задачи многокритериальной(векторной) оптимизации возникает в тех случаях,когда имеется несколько целей, которые не могут быть отражены 1 критерием. Задача многоцелевой оптимизации записывается как векторная задача мат. программирования(ВЗМП):

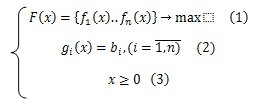
X-вектор, состоящий из n-компонентов (х1…хn) –вектор переменных, обычно неотрицательных (3)

F-множество критериев в виде векторной ЦФ,fj-частный критерии.

Ограничение (2)-функциональная взаимосвязь переменных.Заметим,что изменением знака функции всегда можно свести задачу от min к max.

Необходимо:

1)описать допустимую область(ОДР), определенную ограничениями (2),(3).

2)задать ЦФ(1)

3)указать принцип окончательного решения (L)

Особенностью задач ВЗМП является наличие ОДР области компромисса, в котором невозможно одновременное улучшение всех критериев. Принадлежащие области компромиссов планы называются эффективными или оптимальными по Парето.

В общей формулировке такие задачи могут быть приведены к ситуаций различного содержания, которые можно разделить на 4 типа:

1)задача оптимизации на множестве целей, каждой из которых должна быть учтена при выборе оптимального решения.Пример: задача составления плана работы предприятия с частным критерием-прибыль, затраты, рентабельность.

2)на множестве объектов, качество функционирования каждого из которых оценивается своим критерием. Пример: задача распределения дефицитного ресурса между предприятиями.

3)задача оптимизации на множестве условий функционирования: задан спектр условий, в котором работает объект, условие качества функционирования определяется частным критерием.

4)на множестве этапов функционирования качества управления на каждом этапе оценивается частным критерием, а на множестве этапов- векторным критерием. Пример: задача календарного планирования,задача динамичного программирования.

Обычно в задачах 2),3),4), частный критерий имеет одну размерность.

В задачах 1 типа размерности критериев разные, поэтому не приводят обычно к безразмерному виду путем нормирования критерия.

Существуют и другие классификации.

27. Оптимальность по Парето.

Введем понятие предпочтительности плана:

План х⁰ не хуже х¹, если F_k(x⁰)≥F_k(x¹), где (.Если среди этих неравенств есть хотя бы 1 строгое, то план х⁰ предпочтительнее х¹ , то есть, при переходе от х⁰ к х¹ значение их одного критерия не ухудшилось, и хотя бы 1 критерий улучшился.

План х⁰ оптимален по Парето( эффективен), если он допустим и не существует другого плана х¹ для которого выполняется строгое неравенство. Иногда это множество называется переговорным множеством.

Примеры задач см. в лекции 7.1( Оптимальность по Парето)

28. Проблемы, связанные с решением многокритериальных задач принятия решений. Лексикографическая оптимизация.

При разработке методов решения векторных задач возникают специфические проблемы:

1)Проблема нормализации, когда локальный критерии имеет различные единицы измерения и их нельзя сравнивать. Наиболее распространенным способом является замена абсолютных значений критерии их безразмерными относительными величинами (4):

-для задач оптимизации (4)

или относительными значениями отклонений от оптимальных значений критериев :

(5)

Существуют и другие подходы.

2)проблема выбора принципа оптимизации, т.е. в каком смысле оптимальное решение превосходит все остальные.

3)Проблема учета приоритета критериев ,когда локальный критерии имеет различную значимость. В частности эти коэффициенты могут быть найдены методом МПС-метод парного сравнения.

Если одни ЦФ важнее других, то критерии оптимальности можно определить по лексикографическому порядку. Предполагается, что критерии упорядочены относительно важности. На 1 шаге из множества Парето выделяются решения, имеющие max оценку по самому важному критерию, если такие решение единственное, то оно оптимальное. Если таких решений не одно, то среди них отбирают те, которые имеют max оценку по следующему критерию и т.д.

Пример 3. В подтеме 7.2 (оптимальность по Парето)

29. Методы решения ВЗМП, основанные на свёртывании критериев в единый критерий.

Свертка критериев из локальных в один:

А)аддитивный(наиболее распространенный)-линейная комбинация частных критериев.

Пусть задан вектор весовх коэффициентов α_k , причем Σα_k =1, тогда аддитивный критерии и соответствующая задача –это соотношение (6,7,8):

Здесь частные критерий f_k или имеют одну размерность тлт должны быть привидены к ней для нормализации.

Должны выполняться требования:

1)безразмерности-обеспечивается по ф.(4) или (5)(вопрос 28)

2)степень компромисса с помощью коэффициентов α, которые могут быть найдены методом парного сравнивания.

3)в целях привлечения ЦФ для улучшающих параметров ставится знак +, а для уменьшения знак -.

Пример 4(подтема 7.3,методы решения многокритериальных задач)

Б)мультипликативный – произведение частных критериев в степени α_k:

В отличие от аддитивного нулевое значение хотя бы 1 частного критерия обнуляет ЦФ F(x).

В)комплексного критерия оптимальности

Переход от векторного к скалярному в виде дроби, причем в числителях стоят величины, которые увеличивают эффект( прибыль), а в знаменателе-которые нужно уменьшить (затраты). Тогда имеем показатель рентабельности продукции.

30. Методы решения ВЗМП, использующие ограничения на критерии.

Основные подходы:

Г)метод главной компоненты(ведущего критерия и оптимальности)

Часто переговор-е множество бывает большим, тогда используются приемы, его сужающие.

Идея: все ЦФ, кроме одной переводятся в разряд ограничений. Пусть -вектор с компонентами, равными низким границам критериев, тогда задача имеет вид:

Таким образом, по главному показателю (f₁) реализуется критерий оптимальности, а по остальным-пригодности.

Пример 5 в подтеме 7.3

Д) метод последовательных уступок

Алгоритм:

1)расположить критерии по значимости (наиболее важный f₁)

2)решить задачи по этому критерию (т.е. определить f₁^*)

3)сделать уступку по первому критерию(- определяет ЛПР)

4)решить задачу по критерию

5)процесс повторения для критерия

Окончательный план будет наиболее рациональным: получено оптимальное значение наименее важного критерия при условии гарантирующих значений предшествующие критерии эффективности.

Пример 6 в лекции 7.3

31. Метод идеальной точки в пространстве критериев.

Основной метод целевого программирования – метод идеальной точки. Стремятся найти решение х из множества Паретто, чтобы как можно меньше отклонялся от оптимального значения ЦФ f_k.

В общем виде минимизируются сумма отклонений ЦФ от идеальных значений с весами d_k, т.е. решается однокритериальная задача:

d (F(x);F^--)=[∑α_k│f_k(x)-f_k^--│^p]

F^--- вектор, состоящий

α_к≥0

∑d_k=1

p€[1,∞]

p=1 или 2

d(F(x),F^--)- расстояние(отклонение)

F(x) от F

Точка F обычно не принадлежит ОДР (является внутренней точкой), поэтому её часто называют идеальной или утопической точкой.

Пример 7. Решить задачу из примера 2 методом идеальной точки.

X⁽¹⁾=(1;4) f(X⁽¹⁾)=7

X⁽²⁾=(3;3) f(X⁽²⁾)=9 = F^---(7;9;0)

X⁽³⁾=(3;1) f(X⁽³⁾)=0

Найдем оптимальное решение по каждой ЦФ (графически)

а. для функции f1 оптимальное решение – т. А(1;4). Значение функции в этой точке = 7.

б. для функции f2 оптимальное решение – т. С, т.е. X⁽²⁾=(3;3). Значение в этой точке = 9.

В. Для функции f3 оптимальное решение- т. Д, т.е X⁽³⁾=(3;1). Значение f3=0.

Идеальная точка F имеет координаты: F(7;9;0)

Возьмем р=2. Тогда:H

d=p(F(x);F)= min

Эту задачу можно решить как точку экстремума функции (d^/=0)

По- другому: использовать в EXELE «поиск решений»

Получаем решение:

X^*=(2;97;2;28)

При этом:

f1=1.59;

f2=8.22;

f3=3.87;

Расстояние(миним)

P=6,7

32. Методы решения ВЗМП, основанные на отыскании компромиссного решения.

Принцип гарантированного результата (максимален;минимален)

Рассмотри этот метод на примере 3х функций

F1(x) max

F2(x) max(1)

F3(x) max

qi(x)=bi(2)

x≥0(3)

Решаем задачу по алгоритму:

1.решаем три задачи оптимизации по частным критериям

1.F1(x) max х1* F1 max

2.F2(x) max х2* F2 max

3.F3(x) max х3* F3 max

2. сформулируем задачу минимакса: для безразмерных величин минимизировать мах отклонение 𝜉(эпсилен)

(1) F(α_к,E)=E min

(2)

н.индекс – ЦФ

верх.ин-№ решения

Решаем эту задачу относительно αк и 𝜉

3. Компромиссное решение находим по формулам:

Пояснения: смотри методику

Замечание:

Отклонение компромиссного решения от максимального F1 max не превосходит 𝜉.

Делим все слагаемые на F1 max.

Получаем уравнение 1.

33. Общая задача нелинейного программирования (ОЗНП)

НЛП - случаи математического программирования, в котором ЦФ и / или ограничения являются нелинейной функцией.

В общем случае ОЗНП состоит в определении максимального(минимального) значения функции:

F(x1….x2) (1)

При условиях:

(2)

Где f и g – известные функции

Bi- заданные числа

В результате будет найдена точка x*=(x1*…xn*), координаты которой удовлетворяют системе(2) и такая, что для любой другой точки х*=(х1….хn), удовлетворяющей(2), выполняется неравенство:

f(x1*…xn*)≥f(x1….xn)- для максимума

f(x1*…xn*)≤f(x1….xn)-[≤для минимума]

По аналогии ЗЛП пара ЦФ (1) и связи (2) однозначно определяют ОЗНП.

Если f и gi- мен. Функции, то (1),(2) является ЗЛП

Соотношение (2) могут включать и условия не отрицательности переменных.

В евклидовом пространстве система (2) определяет ОДР, причем, в отличие от ЗЛП, эта область может не выпуклой( выпуклое множество – множество точек таких, что любой отрезок, соединяющий точки, принадлежит этому множеству.

Если определена ОДР, то нахождение решения задачи (1),(2) сводится к определению такой точки этой области, через которую проходит гиперповерхность наивысшего( наинизшего – минимума) уровня.

f(x1…..xn)=h

В отличие от ЗЛП эта точка может находиться и внутри области ОДР.

Как и в ЗЛП , вектор х называется допустимым планом , если он принадлежит ОДР, а если для любого х из ОДР выполняется неравенство:

f(x*)˃f(x)

то х* называется оптимальным планом. В этом случае х* - точка глобального максимума( если выполняется неравенство в окрестности точки х*, то это локальный максимум).

«Бывают задачи линейные – они линейны все одинаково, и бывают задачи нелинейные, каждая не линейна по- своему» Л. Н. Толстой. Поэтому не существует универсального метода решения ЗЛП.

34.Свойства решения ОЗНП

1. ОДР может быть невыпуклым, имеет бесконечное число крайних точек;

2. Экстремум ЦФ может достигать не только на грани, но и внутри ОДР;

3. ЦФ в ОДР может иметь несколько локальных экстремумов.

35.Геометрический метод решения ЗНП. Алгоритм метода.

Процесс нахождения решения ЗНП(1)-(2) с использованием геометрической интерпретации включает следующие этапы:

Алгоритм геометрического метода решения ЗНП.

1.Находим ОДР из соотношений (2) (если она пуста, т.е ограничения не совместимы), то задача не имеет решения;

2.Строят гиперповерхность f(x1…..xn)=h (называют линия уровня) и определяют гиперповерхность наивысшего (наинизшего) уровня или устанавливают неразрешимость задачи из-за неограниченности функции (1) сверху (снизу- на минимум);

3. Находят точку ОДР х*, через которую проходит гиперповерхность наивысшего уровня, и определяют в ней значение функции(1), т.е. f(x*).

36. Метод множителей Лагранжа

Рассмотрим частный случай ОЗНП (1)-(2)

1)1. Система ограничений Условия

2. Содержащий только уравнения (удерживающей связи)

2) Отсутствуют условия не отрицательности переменных х

3) f(x), gi(x)- функции непрерывности вместе со своими частными производными.

Тогда имеем задачу (3)-(4)

В курсе математического анализа задача (3)-(4) называют задачей на условный экстремум или классической задачей оптимизации.

Вводят набор переменных х1,….,хn- называется множителями Лагранжа и составляют функцию Лагранжа (5)

(5) F(x1…xn,x1…xm) = f(x1….xn)-Σλ; bi-gi(xi)]

Находят частные производные и рассматривают систему (n+m) уравнений.

(6)

Любое решение системы (6) относительно х1…..хn; λ1….λm. Определяем точку х₁⁰, в котором может иметь место экстремум функции f.

В дальнейшем исследование таких точек проводится как и в случае безусловного экстремума (см. математику)

Теорема 1

Если х*- точка условного экстремума функции (3) при ограничениях (4) и ранг матрицы первых частей производных функций =m, то существует такие λi, не равные одновременно 0, при которой выполняется в этой точке условие (6). Теорема 1 дает необходимое условие экстремума.

Алгоритм метода множителей Лагранжа.

1. Составляют функцию Лагранжа

2. Находят частные производные функции Лагранжа переменным xj и λi, решают систему уравнений(6) и находят точки, в которых ЦФ может иметь экстремум.

3. Среди этих точек (подозрительных на экстремум) находят те, в которых достигается экстремум и вычисляют значение (3) в этих точках.

[2] Способ(метод множителя Лагранжа)

1. F(x1;x2…. )= 4x1+x²1+8x2+x²2+λ(180-x1-x2). Функция Лагранжа

2.

(а)-(б)

X1=91

X2=85

Точка называется стационарной, в которой градиент функции fград*=0, т.е. является подозрительной на экстремум.

Значение метода Лагранжа заключается в том, что он позволяет перейти о условной оптимизации к безусловной («+») «-» - очень мало задач на практике описываются аналитически (в виде формул). Такие модели называются непрямые. Существуют и прямые методы, основанные на итеративных процессах (см.,например, градиент. Методы в конце темы)

Замечание: Метод множителя Лагранжа можно применять и в случае, когда условия связи представляют собой неравенства (связи). Находят экстремумы функции F; затем отбирают те значения х*, которые удовлетворяют неравенствам( связям); и, наконец, определяют точки , удовлетворяющие системе(6)