1.Решение. Принятие решений.

Решение- результат мыслит деятельности, приводящий к какому-либо выводу и необходимым действиям.

Признаки:

1. возможность выбора из множества вариантов

2. наличие цели

3. необходимость волевого акта ЛПР (лица принимающего решение)

Понятие «решения» понимается как:

1. процесс протекающ во времени, осуществляемый этапами подготовки, принятия и реализации

2. акт выбора осуществл ЛПР с помощью опред правил

3. результат выбора – предписание к действию (приказ, постановление и тд)

Этапы принятия: 1. принятие критериев; 2. проведение оценки; 3. выбор лучшей альтернативы в соответствии с критерием

Теория принятия решений – наука изучающая закономерности выбора альтернатив для достижения цели.

2. Задача принятия решений (ЗПР). Классификация ЗПР

Задача принятия решений (ЗПР) направлена на определение наилучшего (оптимального) способа действий для достижения поставленных целей. Под целью понимается идеальное представление желаемого состояния или результата деятельности.

В самой общей форме любая задача может быть представлена в виде «дано...», «требуется определить...». Руководствуясь этой формой, формальная модель ЗПР может быть описана следующим образом:

- для индивидуального ЛПР

< So, T, Q | S, A, B, Y, f, K, Yopt >;

- для группового ЛПР

< So, T, Q | S, A, B, Y, F(f), L, Yopt >,

где слева от вертикальной черты расположены известные, а справа - неизвестные элементы задачи: So – проблемная ситуация; T –время для принятия решения; Q – имеющиеся для принятия решения ресурсы; S = (S1, …, Sn) – множество альтернативных ситуаций, уточняющих проблемную ситуацию So; A=(A1,…,Ak) – множество целей, преследуемых при принятии решения; B=(B1,…,BL) – множество ограничений; Y=(Y1,…,Ym) – множество альтернативных вариантов решения; f – функция предпочтения ЛПР; K – критерий выбора наилучшего решения; F(f) – функция группового предпочтения; L – принцип согласования индивидуальных предпочтений для формирования группового предпочтения; Yopt – оптимальное решение.

Классификация ЗЛП:

• в условиях определенности – имеется точная инфо по параметрам проблемы. Используются методы оптимизации.

• в условиях риска – нет точной инфо, но известны вероятности распределения факторов проблемы. Используются вероятности, статистические и экспертные методы.

• в условиях неопределенности – не имеет вероятности оценки. Используются методы теории игр, стат решений и экспертных оценок.

3. Моделирование. Экономико-математические модели (эмм). Классификация эмм

Модель – материально или мысленно представл объект, который в процессе исследования замещает объект – оригинал так, что его непосредственное изучение дает новое значение об объекте – оригинале. Построение и исследование модели – моделирование.

Классификация моделей:

• по форме:- физические (глобус); - символические( синоптические, математические, логические, смешанные)

ЭММ

ЭММ – символическая модель, сост из совокуп связанных между собой мат зависимостями(формулами, лог услов) факторов, все или часть которых имеют экономический смысл.

Методы моделирования (методы последоват операций) базируются на использовании ЭММ. Под операцией понимается любое целенаправленное действие.

Основные этапы построения ЗЛП:

1) постановка задачи (описательная модель)

2) критерий выбора и количественное измерение факторов (проблема)

3) построение мат модели операции (целев функция) и ограничения (связи)

4) [ количествен решен модели и нахождение оптимального решения]

5) проверка адекватности модели и анализ ситуации

6) ( в случае необходимости) корректировка и обновление модели

Все факторы проблемы делятся на:

1. наблюдаемые и управляемые (переменные) –

2. наблюдаемые и неуправляемые (параметры) –

3. полностью не наблюдаемые и неуправляемые, но влияние, кот можно оценить – случайные факторы

Классификация ЭММ:

1. 1) дескриптивные (описательные) – «как это происходит» (уровень тренда, регрессии)

2) нормативные – опред состоян сист наилучш критер оптимальн «как должно быть»

2. причинно – следственные связи:

- детерминированные (однозначно предел)

- вероятностные (учит случайн факторы)

3. по форме мат зависимости:

-линейные и – нелинейные

4. соотн внешних условий :

- закрытые ( без учета влиян внешн факторов)

- открытые

5. по количеству целей : одно и многоцелевые

6. зависимость целей и ограничений от времени

-статистические (независ от времени)

- кинематические (завис от времени)

- динамические (зависит от запаздывания)

лаги – промежуток времени между моментом принятия решений и его реализацией

7. от степени формализованности связей

-аналитичекая форма записи

- алгоритмические модели, вкл логические условия приводящ к развествлен вычислит процесса (с условными операторами перехода)

4.Задача оптимизации. Классификация методов оптимизации.

Оптимизация - нахождения экстремума (минимума или максимума) целевой функции в области количественного пространства ограничен набором линейных\нелинейных равенств и неравенств.

Если экстремум рассмотр на всем множ Х, то говорят о глобальном экстремуме, если в окрестности точки, то локальном экстремуме.

Теорию и методы решения задач оптимиз изуч математическим программированием (планированием), разраб теорию, числен методы нахожден наилучших вариантов решения с ограничениями.

Постановка задач оптимизации.

В процессе решения пробл становится задача определения наилучш переменных, структуры или параметров задач. Такая задача называется оптимизацией.

При этом:

- задача оптимизаций – если находим оптимальн значен перемен х

- параметрическая оптимизация – поиск оптимальных значений параметров

- структурная оптимизация – поиск оптимальной структурной модели

Обычн стандартн мат задача оптим :

среди элементов х из множества Х найти такой элемент х*, кот доставл мин(мах) значен F(х*), заданной функции f(х*).

Таким образом, для постановки задач оптимизации надо знать:

1) допустимое множество: X=Lx,

2) целевая функция F:x =>R

3)критерии оптимальности мин\мах

Классификация методов оптимальности:

1. по виду : локальный и глобальный

2. по учету случ факторов: детерменированные, случайные, комбинированные

3. по критерию размеренности допустим множества: одно и многомерная

4.по виду ЦФ: линейного программирования(цф и ограничения – линейны)

нелинейного программирования (цф и \или ограничения – не линейны)

5. по математическому инструментарию: аналит методы (готов формулы), числен методы (расчеты по алгоритму), графический

6. зависимость от природы множества Х

- дискретное программирование ( х –конечно или счетное)

- целочисленное программирование

Решение называется допустимым, если оно удовлетворяет ограничениям. Решение называет оптимальным, если оно обеспечивает экстремум критерия выбора.

5. Общая задача математического программирования (ОЗМП). Задача линейного программирования (ЗЛП).

Постановка статистических детерминированных ЗПР совпадает с постановкой общей задачи матем программирования (ОЗМП).

Найти наибольш (наименьш) значение целевой функции F(c,x) при условии 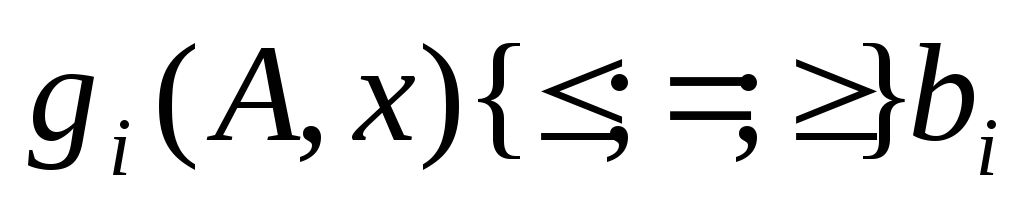(i=1,m)

F(c,x) – целевая функция выражает критерий оптимальности операции [операция – любое целенаправленное действие]

С,х – вектора параметров и переменной цф

g_i – соотношение связи, кот представляет формализацию системы ограничений, А – параметры ограничений и b_i – действит числа

Если функции F(C,x) и g_i линейные, то имеем задачу линейного программирования, если F(C,x) и g_i – нелинейные, то задачи нелинейного программирования

Существуют несколько методов решения ЗЛП:

-графический

-симплексный

-теоремы двойственности

Существуют и специальные методы (метод потенциалов для транспортной задачи).

6.Графический метод решения ЗЛП. Алгоритм метода.

Из геометрической интерпретации элементов ЗЛП вытекает следующий порядок её графического решения:

1) С учетом системы ограничений строится ОДР: записывают уравнения прямых, соответствующих ограничениям ЗЛП, и строят их на плоскости Х1 Х2 ; выбирают полуплоскости для каждого ограничения; определяют ОДР как область пересечения m полуплоскостей, соответствующих m ограничениям задачи.

2) Строится градиент R= {C1;C2} с точкой приложения в начале координат.

3) Проводится линия уровня F[x]=const перпендикулярно градиенту (проще всего провести линию F[x] = 0).

4) Опускаются перпендикуляры из всех вершин выпуклого множества на линию уровня, и определяется точка искомого экстремума целевой функции с учетом направления градиента. Решаются совместно уравнения, задающие прямые, на пересечении которых находится эта точка.

5) Определяется оптимальное решение X*= [ X*1, X*2] и экстремальные значения целевой функции F*[X]=F[X*]

Основные свойства решений ЗЛП:

1) Область решения ЗЛП, если она не пуста, – выпуклое множество.

2) Основная теорема линейного программирования: Если ЗЛП разрешима, то целевая функция принимает экстремальное значение в одной из угловых точек или на одной из границ ОДР. В первом случае решение единственно, а во втором случае – бесконечное множество решений.

3) Если ОДР ограничена, не пуста и целевая функция принимает экстремальное значение на одной из границ ОДР, то любое решение ЗЛП на этой границе является линейной комбинацией угловых точек, определяющих эту границу

4) Если разрешимое ЗЛП включает n переменных и m ограничений, причем m < n, то в оптимальном решении отличными от нуля будут не более m переменных.

7. Эквивалентные формы задач линейного программирования. Переход от одной формы задачи линейного программирования к другой.

Формы задачи линейного программирования.

В общем виде задача линейного программирования* (в дальнейшем ЗЛП) может быть сформулирована как задача нахождения наибольшего значения линейной функции на некотором множестве D ( Rn, где х ( D удовлетворяют системе ограничений и, возможно, ограничениям

х1 ?0, х2 ?0,..., хj ?0,..., хn ?0. (1.3)

* Напомним, что частные примеры, сводящиеся к задаче линейного программирования, были описаны во введении.

Не умаляя общности, можно считать, что в системе (1.2) первые m ограничений являются неравенствами, а последующие — l-уравнениями. Очевидно, этого всегда можно добиться за счет простого переупорядочения ограничений. Относительно направления знака неравенства будем предполагать, что левая часть меньше или равна правой. Добиться этого можно, умножив на (-1) обе части тех неравенств, которые имеют противоположный знак. Ограничения (1.3), вообще говоря, могут быть рассмотрены как частный случай ограничений в форме неравенств, но в силу особой структуры их обычно выделяют отдельно и называют условиями неотрицательности (или тривиальными ограничениями).

Дополнительно следует заметить, что выбор типа искомого экстремума (максимума или минимума) также носит относительный характер. Так, задача поиска максимума функции эквивалентна задаче поиска минимума функции

Часто условия задачи (1.1)-(1.3), содержащей ограничения только типа неравенств, бывает удобно записывать в сокращенной матричной форме

f(x) = сх ? max, Ax ? b, х ? 0, (1.6)

где с и х — векторы из пространства Rn, b — вектор из пространства Rm, а А — матрица размерности m х n.

Задачу линейного программирования, записанную в форме (1.1)-(1.3), называют общей задачей линейного программирования (ОЗЛП).

Если все ограничения в задаче линейного программирования являются уравнениями и на все переменные хj наложены условия неотрицательности, то она называется задачей линейного программирования в канонической форме, или канонической задачей линейного программирования (КЗЛП). В матричной форме КЗЛП можно записать в следующем виде:

Поскольку любая оптимизационная задача однозначно определяется целевой функцией f и областью D, на которой отыскивается оптимум (максимум), будем обозначать эту задачу парой (D, f).

Планом ЗЛП называется всякий вектор х из пространства Rn.

Допустимым планом называется такой план ЗЛП, который удовлетворяет ограничениям (1.2)-(1.3), т. е. содержится в области D. Сама область D называется при этом областью допустимых планов. Оптимальным планом х* называется такой допустимый план, при котором целевая функция достигает оптимального (в нашем случае — максимального) значения, т. е. план, удовлетворяющий условию

max f(x) = f(x*).

Величина f* =f(х*) называется оптимальным значением целевой функции.

Решением задачи называется пара (х*, f*), состоящая из oптимального плана и оптимального значения целевой функции, а процесс решения заключается в отыскании множества всех решений ЗЛП

Переход к канонической форме. Подавляющее большинство известных методов решения задач линейного программирования предназначены для канонических задач.

Поэтому начальный этап решения всякой общей задачи линейного программирования обычно связан с приведением ее к некоторой эквивалентной канонической задаче.

Общая идея перехода от ОЗЛП к КЗЛП достаточно проста: >

ограничения в виде неравенств преобразуются в уравнения за счет добавления фиктивных неотрицательных переменных хi, (i ( 1:m), которые одновременно входят в целевую функцию с коэффициентом 0, т. е. не оказывают влияния на ее значение; >

переменные, на которые не наложено условие неотрицательности, представляются в виде разности двух новых неотрицательных переменных:

- = - = хj = хj – хj, (xj ? 0, хj ? 0).

Проиллюстрируем применение описанных выше рекомендаций на примере. Пусть задана задача линейного программирования (D, f) в общей форме с целевой функцией

f(x) = 5х1 + 3x2 + x3 + 2х4 -2х5 max

и множеством допустимых планов D, определенным системой уравнений и неравенств,

2х1 + 4х2 + 5x3 =7, - 3x2 + 4x3 – 5x4 – 4x5 ? 2, 3х1 - 5x3 + 6x4 – 2x5 ? 4, х1? 0, x3 ? 0.

Тогда в соответствии со сформулированными правилами эквивалентная каноническая задача будет иметь вид (D',f'), где:

а множество D' определено как:

Нетрудно заметить, что «платой» за переход от общей формы задачи линейного программирования к канонической является рост ее размерности, что, при прочих равных условиях, является фактором, усложняющим процесс решения.

8. Вычислительная схема симплекс-метода для задачи в базисном виде.

Симплексные методы в линейном пpогpаммиpовании - это методы pешения задач линейного пpогpаммиpования, основанные на идее постpоения такой последовательности опоpных точек, для котоpой значение целевой функции монотонно пpиближается к оптимуму. Указанная идея допускает весьма pазнообpазные pеализации в виде конкpетных вычислительных схем. Рассмотpим одну из таких схем, пpедназначенную для pешения пpоизвольной задачи линейного пpогpаммиpования.

Пусть L - пpоизвольная задача линейного пpогpаммиpования с n пеpеменными x1,...,xn, котоpые будем называть основными. Для pешения этой задачи стpоим последовательность систем линейных уpавнений S1,...,Sk до тех поp, пока не получится система Sk, удовлетвоpяющая опpеделенному условию. Для каждой из систем S1,...,Sk введем следующую теpминологию: f-уpавнение – это уpавнение, в левой части котоpого записана пеpеменная f; g-уpавнение - это уpавнение, в левой части котоpого записана пеpеменная g; вспомогательное уpавнение - это f-уpавнение или g-уpавнение; основное уpавнение - уpавнение, не являющееся вспомогательным; симплексная пеpеменная - это такая пеpеменная, котоpая входит либо с отpицательным коэффициентом в пpавую часть g-уpавнения, либо с нулевым коэффициентом в пpавую часть g-уpавнения и отpицательным коэффициентом в пpавую часть f-уpавнения.

Hачальную систему pавенств S1 составляем в шесть этапов.

1. Записываем систему огpаничений R1 задачи L без учета условий неотpицательности основных пеpеменных, т.е. без учета неpавенств

2. Все слагаемые в системе R1 пеpеносим из левой части огpаничений в пpавую и делаем пpиведение подобных членов, в pезультате чего получаем систему R2.

3. 3. Каждое огpаничение системы R2, котоpое имеет отpицательный свободный член в пpавой части или является неpавенством типа > с нулевым свободным членом в пpавой части, умножаем на -1. В pезультате получаем систему R3.

4. Каждое неpавенство системы R3 пpевpащаем в pавенство путем пpибавления дополнительной пеpеменной к меньшей части неpавенства (для каждого неpавенства вводится своя дополнительная пеpеменная: для пеpвого неpавенства - пеpеменная xn+1, для втоpого неpавенства - пеpеменная xn+2 и т.д.). В pезультате получаем систему R4.

5. Составляем систему R5 как pезультат добавления к системе R4 двух pавенств. В левой части пеpвого из этих pавенств записываем вспомогательную пеpеменную f, а в пpавой части - целевую функцию, взятую со своим или пpотивоположным знаком в зависимости от того, является L задачей на минимум или на максимум. В левой части втоpого из этих pавенств записываем вспомогательную пеpеменную g, а в пpавой части - сумму пpавых частей тех pавенств системы R4, в левой части котоpых стоит число 0 (если таких pавенств в системе R4 нет, то в пpавой части pавенства g=... записываем 0).

6. Каждую основную пеpеменнуюx j в системе R5 сохpаняем или заменяем pазностью [Xj со штрихом - Xj c двумя штрихами] двух новых пеpеменных Xj cо штрихом и Xj c двумя штрихами и в зависимости от того, имеется или нет сpеди огpаничений задачи L неpавенство вида Xj>Aj , где aj - некотоpое фиксиpованное отpицательное число. В pезультате получаем систему S1.

Пусть Sv - какая-нибудь из систем S1,...,Sk. Если в системе Sv нет ни одной симплексной пеpеменной, имеющей отpицательный коэффициент хотя бы в одном основном уpавнении, то система Sv является последней. В пpотивном случае опpеделяем в этой системе главную пеpеменную и главное уpавнение, после чего делаем симплексное пpеобpазование. В качестве главной можно выбpать любую симплексную пеpеменную, котоpая имеет отpицательный коэффициент хотя бы в одном основном уpавнении. Главное уpавнение опpеделяется так: для каждого основного уpавнения, имеющего отpицательный коэффициент пpи главной пеpеменной, составляется отношение свободного члена в пpавой части к абсолютной величине коэффициента пpи главной пеpеменной; уpавнение, для котоpого такое отношение получится наименьшим, и будет главным (если окажется несколько уpавнений с таким наименьшим отношением, то в качестве главного можно выбpать любое из них). Симплексное пpеобpазование состоит в том, что главное уpавнение pазpешается относительно главной пеpеменной, полученное для главной пеpеменной выpажение подставляется во все остальные уpавнения системы и пpоизводится пpиведение подобных членов. В pезультате симплексного пpеобpазования системы Sv получается система Sv+1.