
- •0. Введение
- •I. Теоретический раздел
- •1. Основные определения
- •2. Геометрическое изображение комплексного числа. Понятие о модуле и аргументе
- •3. Умножение и деленин комплексных чисел в тригонометрической и покзательной форме
- •4. Возведение в степень и извлечение корня из комплексного числа
- •II. Справочный раздел
- •1. Табличные значения аргументов некоторых комплексных чисел
- •3. Формулы для степеней и корней
- •III. Практический раздел Образцы решения задач и их оформления
0. Введение
Эволюционный процесс появления комплексных чисел связан с математическими действиями. Каждому математическому действию соответствует обратное действие: сложению – вычитание, умножению – деление, возведению в целую положительную степень – извлечение корня.
Сумма любых двух
натуральных чисел является натуральным
числом. Следовательно, прямое действие
– сложение, не выводит нас за пределы
множества натуральных чисел
![]() .
Однако обратное действие – вычитание,
выводит нас за пределы этого множества.
Действительно, результаты следующих
разностей:
.
Однако обратное действие – вычитание,
выводит нас за пределы этого множества.
Действительно, результаты следующих
разностей:![]() ,
,![]() не являются натуральными числами, то
есть действие вычитание не выполнимо
в множестве натуральных чисел.
не являются натуральными числами, то
есть действие вычитание не выполнимо
в множестве натуральных чисел.
Действие вычитание
становится выполнимым, если к множеству
натуральных чисел присоединить нулевое
число и все целые отрицательные числа.
Полученное множество называется
множеством
целых чисел
![]() .
На множестве целых чисел выполнимы оба
действия: прямое – сложение и обратное
– вычитание. Таким образом, желание
выполнить действие вычитание, привело
нас к расширению множества натуральных
чисел до множества целых чисел.
.
На множестве целых чисел выполнимы оба
действия: прямое – сложение и обратное
– вычитание. Таким образом, желание
выполнить действие вычитание, привело
нас к расширению множества натуральных
чисел до множества целых чисел.
На множестве целых
чисел выполнимо также прямое действие
– умножение. Обратное действие – деление
выводит нас за пределы множества целых
чисел. Чтобы и действие деление было
возможным нужно к множеству целых чисел
присоединить все несократимые дроби.
Полученное множество называется
множеством
рациональных чисел
![]() .
Множество рациональных чисел замкнуто
относительно всех четырех арифметических
действий, то есть в результате сложения,
вычитания, умножения и деления (кроме
деления на 0) рациональных чисел, опять
получится рациональное число. Если
ограничиться этими действиями и решением
линейных уравнений и систем, то множество
рациональных чисел является полным.
.
Множество рациональных чисел замкнуто
относительно всех четырех арифметических
действий, то есть в результате сложения,
вычитания, умножения и деления (кроме
деления на 0) рациональных чисел, опять
получится рациональное число. Если
ограничиться этими действиями и решением
линейных уравнений и систем, то множество
рациональных чисел является полным.
На языке десятичных дробей рациональными числами являются такие десятичные дроби, которые либо конечные, либо бесконечные периодические.
Дальнейшее
расширение числовых множеств связано
с нелинейными уравнениями и, в первую
очередь, с квадратными. Рассмотрим
квадратное уравнение
![]() .
В множестве рациональных чисел это
уравнение не имеет решения, хотя его
дискриминант
.
В множестве рациональных чисел это
уравнение не имеет решения, хотя его
дискриминант![]() является положительным. Следующее наше
желание состоит в том, чтобы все квадратные
уравнения с положительными дискриминантами
имели решения. Это приводит нас к понятию
иррациональных чисел.
является положительным. Следующее наше
желание состоит в том, чтобы все квадратные
уравнения с положительными дискриминантами
имели решения. Это приводит нас к понятию
иррациональных чисел.
Иррациональными
числами
называются бесконечные десятичные
непериодические дроби. Множество
иррациональных чисел обозначим
![]() .
В множестве иррациональных чисел
уравнение
.
В множестве иррациональных чисел
уравнение![]() имеет решение:
имеет решение:![]() .
Это число не является рациональным.
Действительно, предполагая противное,
получим, что существует несократимая
простая дробь
.
Это число не является рациональным.
Действительно, предполагая противное,
получим, что существует несократимая
простая дробь![]() такая, что
такая, что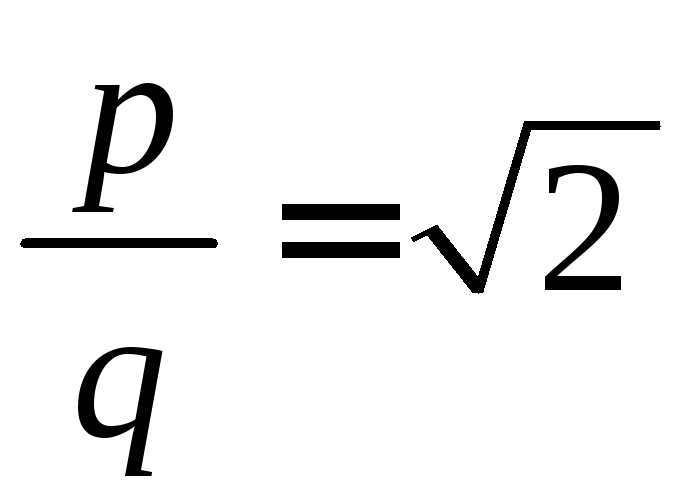 ,
где
,
где![]() и
и![]() – взаимно простые натуральные числа.
Умножив на
– взаимно простые натуральные числа.
Умножив на![]() и возведя в квадрат обе части полученного
равенства, будем иметь:
и возведя в квадрат обе части полученного
равенства, будем иметь:
![]() .
.
Правая часть
последнего равенства является четным
числом, следовательно, число
![]() – четное, то есть
– четное, то есть![]() ,
где
,
где![]() – натуральное число Тогда
– натуральное число Тогда
![]() .
.
Левая часть
последнего равенства является четным
числом, следовательно, число
![]() – четное, то есть
– четное, то есть![]() ,
где
,
где![]() – натуральное число. Тогда дробь
– натуральное число. Тогда дробь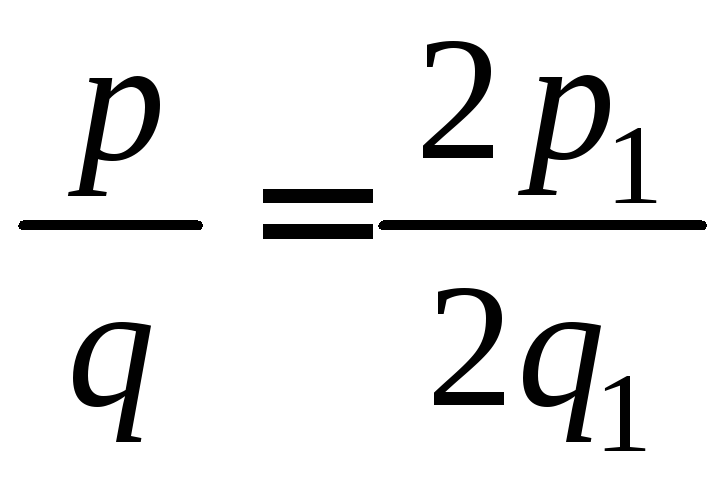 является сократимой. Это противоречит
нашему предположению, что дробь
является сократимой. Это противоречит
нашему предположению, что дробь![]() не является сократимой.
не является сократимой.
Из определения
рациональных и иррациональных чисел
следует, что множества рациональных
чисел
![]() и иррациональных чисел
и иррациональных чисел![]() не имеют общих элементов.
не имеют общих элементов.
Объединение
множества рациональных чисел с множеством
иррациональных чисел называется
множеством
вещественных
или действительных
чисел
![]() .
Следовательно, число называется
вещественным или действительным, если
оно либо рациональное число, либо
иррациональное. На множестве вещественных
чисел имеют решения все квадратные
уравнения с неотрицательными
дискриминантами. Остается рассмотреть
только один случай, а именно, случай с
отрицательным дискриминантом. Простейшим
квадратным уравнением с отрицательным
дискриминантом является
.
Следовательно, число называется
вещественным или действительным, если
оно либо рациональное число, либо
иррациональное. На множестве вещественных
чисел имеют решения все квадратные
уравнения с неотрицательными
дискриминантами. Остается рассмотреть
только один случай, а именно, случай с
отрицательным дискриминантом. Простейшим
квадратным уравнением с отрицательным
дискриминантом является![]() .
Отсюда, получаем
.
Отсюда, получаем![]() .
Так как квадрат любого вещественного
числа
.
Так как квадрат любого вещественного
числа![]() удовлетворяет неравенству
удовлетворяет неравенству![]() ,
то уравнение
,
то уравнение![]() на множестве вещественных чисел не
имеет решения. Вводится новое число
на множестве вещественных чисел не
имеет решения. Вводится новое число![]() ,
называемоемнимой
единицей и
обладающее свойством
,
называемоемнимой
единицей и
обладающее свойством
![]() .
Формально мнимая единица записывается
в виде
.
Формально мнимая единица записывается
в виде![]() .
Используя это обозначение, мы расширяем
также область определения и область
значений квадратного корня. Можно теперь
извлекать квадратный корень из любого
отрицательного числа. Например,
.
Используя это обозначение, мы расширяем
также область определения и область
значений квадратного корня. Можно теперь
извлекать квадратный корень из любого
отрицательного числа. Например,![]() .
Решение же произвольного квадратного
уравнения
.
Решение же произвольного квадратного
уравнения![]() с отрицательным дискриминантом приводит
нас к числам вида
с отрицательным дискриминантом приводит
нас к числам вида![]() ,
где
,
где![]() и
и![]() суть вещественные числа. Такие числа
называютсякомплексными.
Множество
комплексных чисел
обозначается
суть вещественные числа. Такие числа
называютсякомплексными.
Множество
комплексных чисел
обозначается
![]() .
.
В предлагаемом пособии приводятся основные понятия, связанные с комплексными числами и изучаются их основные свойства.
