Elektrichesky_privod_Kosmatov_V_I_2012

При активном моменте M с переходный процесс при <0 про-

должается уже под действием активного момента M с , время переход-

ного процесса составит tп (3 4)Т М ; при M с реактивном – про-

цесс торможения заканчивается при 0 .

7.2.3. Переходные процессы в асинхронном электроприводе с нелинейными механическими характеристиками

Зависимости f (t) или s f (t) являются нелинейными и

где M к и sк критический момент и критическое скольжение,

На рис. 7.11 представлена схема прямого пуска асинхронного двигателя с короткозамкнутым ротором и механические характеристики при пуске.

200

Рис. 7.11. Схема (а) и механическая характеристика (б), графики переходных процессов (в)

Принципиальная схема (рис. 7.11,а) содержит асинхронный короткозамкнутый двигатель М с моментом инерции J, автоматический выключатель QF, трехфазный линейный контактор KM, две кнопки SB1 (пуск) и SB2 (стоп), тепловое реле KK, плавкие предохранители FU. Контактор и тепловое реле обычно конструктивно объединены в одном аппарате – магнитном пускателе.

Нажатием кнопки SB1 при включенном QF катушка контактора KM получает питание, замыкаются контакты KM в силовой цепи статора и к обмотке статора подводится напряжение сети. Двигатель разгоня-

ется по характеристике f (М ) (рис. 7.11,б), включенный контакт

КМ заблокирует кнопку SB1, тем самым обеспечивая питание катушки КМ после отпускания кнопки SB1.

Нажатие на кнопку SB2 обесточивает катушку контактора КМ, двигатель отключается от сети и тормозится моментом статической на-

грузки M с или находится на свободном выбеге.

201

Защита от перегрузки осуществляется автоматически выключателем QF, который должен отстроен от пускового тока; от тепловой перегрузки и обрыва фазы – с помощью теплового реле КК.

Это простейшая схема, осуществляющая только пуск двигателя; в справочниках можно найти варианты этой схемы с добавленными функциями – динамического торможения, торможения противовключением и реверса.

Переходные функции f (t) , M f (t) в режимах пуска, торможения и реверса, несмотря на нелинейность f (t) , можно рассчитать и построить аналитическим методом; кроме того можно произвести анализ влияния сопротивления роторной цепи R2' на пока-

затели переходного процесса.

Для упрощения математических выкладок при решении поставленной задачи принимается, что в переходных процессах M с 0 . То-

гда уравнение движения электропривода может быть представлено в следующем виде

После интегрирования окончательное выражение для определения времени переходного процесса пуска, торможения, реверса может

быть представлено в относительных единицах

Физический смысл TM – это время, в течении которого асинхронный двигатель разгонится из неподвижного состояния до скорости 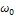под действием неизменного критического момента M к , что нагляд-

но поясняется графиками (штриховыми линиями) на рис. 7.11,б. Рассмотрим на примерах количественные соотношения в пере-

ходных процессах асинхронного электропривода без учѐта электромагнитной инерции.

Пример 1. Переходные процессы при пуске ( M c 0 )

В этом случае sнач 1, sкон 0,05 (см. рис. 7.11,б), время пуска после подстановки этих значений в уравнение (7.27) определится

skопт 0,408 .

203

После подстановки этого значения в формулу (7.28) имеем

т.е. минимальное время пуска при skопт 0,408 всего на 22% боль-

ше TM . Момент пусковой эффективный

При skопт 0,408

М Пэфmax 0,81M к .

Таким образом, для электроприводов, работающих с частыми пусками, необходимо применять асинхронные двигатели с повышен-

ным критическим скольжением ( sk 0,3 0,4 ).

Пример 2. Переходные процессы при торможении противовклю-

чением ( M c 0 ).

Для осуществления торможения противовключением необходимо изменить чередование фаз с А,В,С, например, на В,А,С . При этом момент двигателя становится тормозным

Производная от (7.30)

dtП / TM 0 dsк

позволяет определить

При sкопт 1,47

M Tээ m a x 0.98M к .

Зависимости, представленные на рис. 7.12,б и 7.12,в, соответст-

вуют 1 - sкопт = 0,408; 2 - sк =0,2; 3 - sк =0,8.

Методика расчѐта переходных процессов такая же, что и при

пуске.

Пример 3. Динамическое торможение ( M c 0 )

Как известно, для осуществления динамического торможения асинхронного электропривода статор двигателя отключается от сети переменного тока и в его обмотку подаѐтся постоянный ток.

205

где TM .T - электромеханическая постоянная времени электропривода при динамическом торможении;

sнач 1 - начальное скольжение при торможении sкон 0,05 - конечное скольжение.

Рис. 7.13. Схема (а), механические характеристики (б) и переходные процессы при sкопт 1,47 (в)

207

Окончательно время торможения определится

критическом скольжении sк.т 0,408 .

Так как критическое скольжение при динамическом торможении асинхронных двигателей с короткозамкнутым ротором значительно меньше, чем значения в двигательном режиме, можно принять, что

найти эквивалентный ток статора, который связан с величиной постоянного тока, подаваемого в статор

Кроме того, если учесть, что индуктивное сопротивление намагничивающего контура x 0 << x2' , формулу (7.35) можно представить в виде

208