
Uch_posobie_TMM
.pdf
40
систем координат в плоскости определяется уравнениями вида:
|
|
|
|
|
x0 |
= a + x1 m11 |
+ y1 m12 |
, |
|
|
|
|
|
|
y0 |
= b + x1 m21 |
+ y1 m22 |
, |
(2.15) |
где x1, y1 |
- координаты точки в системе X1Y1 ; |
|
|
||||||
x0 |
, y0 |
- координаты точки в системе X0Y0 ; |
|
|
|||||
a, |
b |
|
- координаты точки O1 в системе X0Y0 |
; |
|||||
m11 |
= cos (X0 |
^X1); |
m12 = cos (X0^Y1); m21 = cos (Y0^X1); |
||||||
m22 |
= cos (Y0 |
^Y1) |
- |
направляющие косинусы. |
|||||
Система уравнений (2.15) может быть записана в эквивалентной матричной форме:
x |
|
a |
+ |
m |
m |
|
x |
|
, |
|
0 |
|
= |
|
11 |
12 |
|
1 |
|
||
y |
|
|
|
|
m |
m |
|
y |
|
|
0 |
|
b |
|
21 |
22 |
|
1 |
|
|
|
где x0 |
|
= X0 - матрица-столбец координат точки в системе X0Y0; |
|||||
y |
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
x |
|
|
= |
X1 - |
матрица-столбец координат точки в системе X1Y1; |
||
|
1 |
|
|||||
y |
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
a |
|
= |
L10 - матрица-столбец параллельного переноса начала ко- |
||||
|
|
|
|||||
b |
|
|
|
|
|
||
ординат системы X1Y1 в начало координат системы X0Y0; |
|||||||
m |
|
|
m |
|
|
V10 – квадратная матрица поворота системы коорди- |
|
|
11 |
|
12 |
= |
|||
m |
|
|
m |
|
|
|
|
|
21 |
|
22 |
|
|
||
нат X1Y1 |
относительно системы X0Y0 . |
||||||
Получим |
|
X0 |
= L10 + V10 X1 . |
||||
В общем виде(2.16)X i - 1 = Li , i - 1 + Vi , i - 1 X i
Последовательные преобразования ряда систем координат производятся следующим образом. Пусть, например, необходимо произвести
преобразования координат точки А из системы |
X3Y3 в систему X2Y2 , |
затем в систему X1Y1 и далее в систему X0Y0 |
(рис. 2.14). |
|
|
41 |
|
|
Y0 |
|
Y3 |
|
|
|
|
|
X3 |
|
yOA |
Y2 |
|
A |
|
y |
x3A |
|
||
Y1 |
b2 |
3A |
|
|
|
O |
|
|
|
|
O |
3 |
|
|
|
X1 |
|
|
|
b1 |
2 |
a2 |
X2 |
|
b |
a1 |
|
||
O1 |
|
|
|
|
O |
a |
|
xOA |
X0 |
|
|
|||
Рис. 2.14. Схема расположения точки в координатных системах |
||||
Согласно выражению (2.16) составляем уравнение преобразования системы X3Y3 в систему X2Y2 :
X2 = L32 + V32 X3 ; |
|
|
|
|||
системы X2Y2 в систему X1Y1 |
: |
|
|
|
|
|
X1 = L21 + V21 X2 ; |
|
|
|
|||
системы X1Y1 в систему X0Y0 |
: |
|
|
|
|
|
X0 |
= L10 + V10 X1 . |
|
|
|
||
Объединив эти выражения, получим |
|
|
|
|
|
|
X0 = L10 + V10 L21 + V21 |
|
L32 + V32 X3 |
|
. |
|
|
В общем виде |
|
|
|
|
|
|
X0 = L10 + V10 … Ln-1, n-2 + Vn-1, n-2 |
|
Ln,n-1 + Vn,n-1 |
Xn |
|
. |
|
(2.17) |
|
|
|
|
|
|
Полученные результаты распространяются на замкнутые и незамкнутые кинематические цепи. Замкнутые кинематические цепи могут быть одно- и многоконтурными. Какова бы ни была одноконтурная кинематическая цепь, с каждым ее звеном связывается система координат XiYi ( i = 1, 2, 3, … , n, где n – число звеньев).
Если произвести последовательные преобразования систем координат вдоль замкнутого контура звеньев, начиная с некоторого звена или, иначе говоря, с некоторой системы координат, и вернуться к исход-
42
ному звену (к исходной системе координат), то такое преобразование будет являться тождественным. Уравнение (2.17) является уравнением замкнутости контура кинематической цепи.
В кинематических цепях плоских механизмов наибольшее распространение получили кинематические пары 5 класса: поступательные и вращательные. Рассмотрим преобразование систем координат в этих кинематических парах.
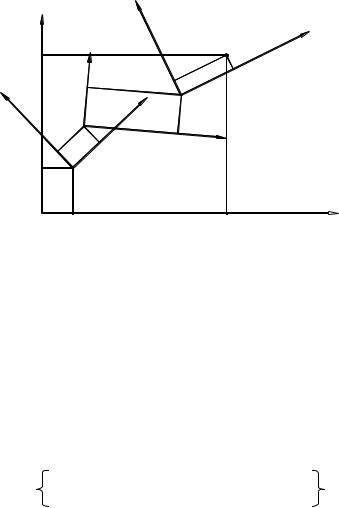
На рис. 3 представлено схематическое изображение поступательной кинематической пары, образованной звеньями i-1 и i, с которыми связаны плоские системы координат Xi-1Yi-1 и XiYi . Соответствующие координатные оси параллельны.
yi-1 |
|
y |
|
|
a |
i |
|
|
|
|
|
|
|
|
xi |
|
i-1 |
Oi |
i |
|
|
b |
|
|
|
|
|
Oi-1 |
|
xi-1 |
|
|
Рис. 2.15. Поступательная кинематическая пара |
||
Уравнение преобразования |
координат |
из |
системы |
XiYi |
в систе- |
||||||
му Xi-1Yi-1 |
будет аналогично выражению (2). Матрицы Vi,i-1 |
и Li,i-1 |
|||||||||
будут иметь следующий вид: |
|
|
|
|
|
|
|
|
|
||
|
|
cos(x |
,^x |
) |
cos(x |
,^y |
) |
|
|
||
|
Vi,i-1 |
= |
i -1 |
i |
) |
|
i -1 |
i |
|
= |
|
|
|
cos(y |
,^x |
cos(y |
,^y |
) |
|
|
|||
|
|
|
i -1 |
i |
|
|
i -1 |
i |
|
|
|
|
|
сos 0 |
cos 90o |
= |
1 |
0 |
|
|
|
||
|
= |
|
|
|
|
|
; |
|
|
|
|
|
|
|
cos 0 |
|
|
0 |
1 |
|
|
|
|
|
cos 90o |
|
|
|
|
|
|||||
43
a Li,i-1 = b .
Получаем уравнение преобразования в матричной форме:
x |
|
= |
a |
+ |
x |
= |
a xi |
|
|
i-1 |
|
|
|
i |
|
. |
|||
y |
|
|
|
|
|
y |
|
|
|
i-1 |
|
|
b |
|
i |
|
b yi |
||
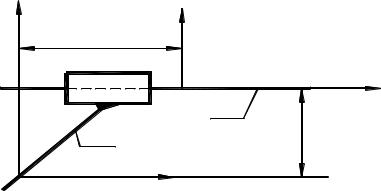
На рис. 2.16 представлено схематическое изображение вращатель-
ной кинематической пары, составленной звеньями i-1 |
и i. Со звеньями |
||
связаны системы координат Xi-1Yi-1 |
и XiYi . Оси Xi-1 |
и |
Xi направлены |
вдоль соответствующих звеньев. Начало координат Оi |
системы XiYi |
||
расположено в центре кинематической пары. |
|
|
|
yi-1 |
xi-1 |
|
|
yi-1
a
Oi-1

 yi
yi




 Oi i
Oi i
 i-1
i-1
xi
Рис. 2.16. Вращательная кинематическая пара
Угол - угол поворота в кинематической паре. Уравнение преобра-
зования координат во вращательной паре также соответствует выражению (2.16). Матрицы Vi,i-1 и Li,i-1 будут иметь следующий вид:
Vi,i-1= |
cos |
cos(270o |
) = cos |
-sin |
; |
|
cos( 90 ) |
cos |
|
sin |
cos |
|
|
|
o |
|
|
|
|
|
44
α Li,i-1 = 0 .
Получаем уравнение преобразования в матричной форме:
xi-1 |
|
|
cos |
-sin |
xi |
|
x cos - y sin |
|||||
|
|
= |
|
|
+ |
|
|
|
= |
i |
i |
|
y |
|
|
0 |
|
sin |
cos |
y |
|
|
x sin |
y cos |
. |
|
|
|
|
|||||||||
i-1 |
|
|
|
|
|
|
i |
|
i |
i |
|
|
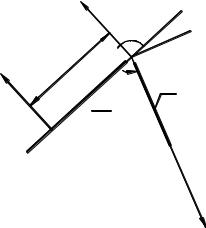
При рассмотрении вращательной пары удобно начала координат Оi-1 и Оi совмещать с центром пары (рис. 5). Тогда матрица Vi-1 будет
иметь прежний вид, а матрица Li,i-1 будет равна 0.
0 Li,i-1 = 0 .
yi-1 yi xi-1
|
Oi-1 |
(O i ) |
|
i-1
i 
 xi
xi
Рис. 2.17. Вращательная кинематическая пара (оси координат расположены в центре пары)
Уравнение преобразования в матричной форме будет определяться следующим образом:
x |
|
|
|
-sin |
|
x |
|
|
x cos - y sin |
||||
|
i-1 |
|
= cos |
|
|
|
i |
= |
i |
i |
. |
||
|
i-1 |
|
sin |
cos |
|
y |
|
x sin |
y cos |
||||
y |
|
|
|
|
|
|
|
i |
i |
|
|||
|
|
|
|
|
|
|
|
|
i |
|
|
||
2.4.2. Преобразование координат точки в пространственных механизмах
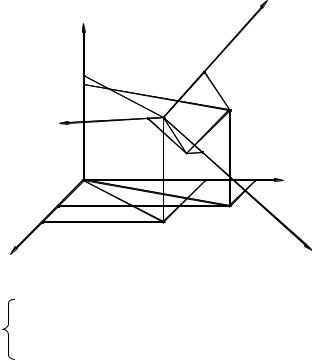
Рассмотренный выше принцип преобразования координат точки в
45
плоских системах справедлив и для пространственных механизмов. Однако, система уравнений, определяющих преобразование координат точки в пространстве из системы X1Y1Z1 в систему X0Y0Z0 (рис. 2.18) будет выглядеть следующим образом:
Z 0 |
|
|
Z1 |
|
|
|
|
c |
z1 |
|
|
|
|
|
|
z0 |
|
A |
|
X1 |
O1 |
|
|
x1 |
|
|
|
|
y1 |
y0 |
Y0 |
O |
b |
||
x0 |
|
|
|
a |
|
|
|
X 0 |
Y1 |
Рис. 2.18. Схема расположения пространственных систем координат
x0 |
= a + x1 m11 |
+ y1 m12 |
+ z1 m13 , |
y0 |
= b + x1 m21 |
+ y1 m22 |
+ z1 m23 |
z0 |
= c + x1 m31 |
+ y1 m32 |
+ z1 m33 |
, ( 2.18 )
,
где x1, y1, z1 |
- координаты точки в системе X1Y1Z1; |
|
||||||||
x0, |
y0, |
z0 |
- координаты точки в системе X0Y0Z0; |
|
||||||
a, b, c |
- координаты точки O1 |
в системе X0Y0Z0; |
||||||||
m11 |
= cos (X0 |
^X1); |
m12 |
= cos (X0 |
^Y1); |
m13 |
= cos (X0 |
^Z1); |
||
m21 |
= cos (Y0 |
^X1); |
m22 |
= cos (Y0 |
^Y1); |
m23 |
= cos (Y0 |
^Z1); |
||
m31 |
= cos (Z0^X1); |
m32 |
= cos (Z0^Y1); |
m33 = cos (Z0^Z1) - направляю- |
||||||
щие косинусы. |
|
|
|
|
|
|
|
|||
Матричная форма записи системы уравнений (2.18) имеет вид:
x |
|
|
|
|
0 |
|
|
y |
|
= |
|
|
0 |
|
|
z |
|
|
|
0 |
|
|
|
ab +c
m11m21m31
m |
m |
|
|
12 |
13 |
|
|
m |
m |
|
|
22 |
23 |
|
|
m |
m |
|
|
32 |
33 |
|
|
x1y1 ,z1
|
|
|
|
46 |
x |
|
|
|
|
|
0 |
|
|
|
где y |
|
= X0 - матрица-столбец координат точки в системе X0Y0Z0; |
||
|
|
0 |
|
|
z |
|
|
|
|
|
0 |
|
|
|
x1
y1 = X1 - матрица-столбец координат точки в системе X1Y1Z1;
z1
a
b = L10 - матрица-столбец параллельного переноса начала ко-
c
ординат системы X1Y1Z1 в начало координат системы X0Y0Z0;
m11m21m31
m12 m22 m32
m13
m23 = V10 – квадратная матрица поворота систе- m33
мы координат X1Y1Z1 относительно системы X0Y0Z0.
2.4.3. Кинематический анализ плоских рычажных механизмов 2-го класса
Рассмотрим последовательность проведения кинематического анализа плоских четырехзвенных механизмов, в состав которых входят структурные группы 2-го класса.
Четырехзвенный механизм структуры 1- 2(1):
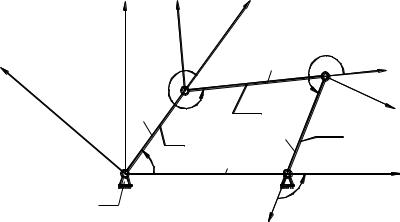
На рис. 2.19 представлена схема кривошипно-коромыслового механизма, состоящего из стойки 0, входного звена 1, звеньев 2 и 3, образующих структурную группу 2-го класса 1-го вида.
|
|
|
47 |
|
|
Y0 |
Y |
|
X1 |
|
|
2 |
|
|
|
|
|
Y1 |
|
|
l2 |
2 |
X2 |
1 |
B |
|
|||
|
|
C |
|
||
|
l1 |
|
2 |
Y3 |
|
|
|
3 |
|||
|
1 |
|
l3 |
|
|
|
|
l0 |
|
|
|
A |
0 |
|
A |
X0 |
|
|
|
|
|
|
|
O |
|
|
|
3 |
|
|
|
|
X3 |
|
|
Рис. 2.19. Кривошипно-коромысловый механизм |
|
||||
На рисунке l0, l1, l2 и l3 - размеры звеньев. Со звеньями 0, 1, 2 и 3 связаны системы координат X0Y0 , X1Y1 , X2Y2 и X3Y3 . Начала координат систем расположены в центрах кинематических пар А, В и С.
Уравнение преобразования координат для данной кинематической цепи будет иметь вид:
|
|
|
|
X0(D) |
= V10 |
|
L21 + V21 L32 + |
V32 X3(D) |
, |
|||
(2.19) |
|
|
|
|
|
|
|
|
|
|
|
|
где X3(D) |
x3(D ) |
|
= |
l |
|
- матрица-столбец координат точки D в |
||||||
= |
|
|
|
|
3 |
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
|
|
|
0 |
|
|
|
|||
|
|
|
3(D ) |
|
|
|
|
|
|
|
||
системе X3Y3; |
|
|
|
|
|
|
|
|
|
|
||
X0(D) = |
x0(D ) |
|
l |
|
- матрица-столбец координат точки D в систе- |
|||||||
|
|
|
= |
0 |
|
|||||||
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
y0(D ) |
|
|
|
|
|
|
|||||
ме X0Y0 .
Матрицы поворотов во вращательных парах и параллельных пере-
48
носов вдоль звеньев при переходе от одной системы координат к другой будут определяться следующим образом:
V32 |
= сos 2 |
-sin 2 |
; |
L32 |
= |
2 |
; |
|||||||
|
|
|
|
|
|
|
|
|
|
|
l |
|
|
|
|
|
|
|
|
cos |
|
|
|
|
|
|
0 |
|
|
|
sin |
|
|
|
|
|
|
|
|
|
|
|||
|
|
2 |
2 |
|
|
|
|
|
|
|
|
|
||
V21 |
|
|
|
|
-sin 1 |
|
|
; |
L21 |
l |
|
; |
||
= сos 1 |
|
|
= |
1 |
|
|||||||||
|
|
|
|
|
cos 1 |
|
|
|
|
|
|
0 |
|
|
|
sin 1 |
|
|
|
|
|
|
|
|
|
|
|||
V10 |
|
сos |
0 |
-sin |
0 |
|
|
|
|
|
|
|||
= |
|
|
cos |
|
. |
|
|
|
|
|||||
|
sin |
0 |
0 |
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
||||
Произведя действия над матрицами согласно выражению (2.19), получим систему уравнений:
l1cos 0 + l2cos( 0 1 ) + l3cos( 0 1 2 ) = l0 ,
l1sin 0 + l2sin( 0 1 ) + l3sin( 0 1 2 ) = 0 . (2.20)
Кроме того, необходимо учесть, что сумма внутренних углов четырехугольника равна 2· , т.е.
0 1 π 2 π 3 2 π,
или
|
|
|
2 |
4 π. |
(2.21) |
0 |
1 |
|
3 |
|
Решая систему уравнений (2.20) с учетом (2.21), получаем зависимости
|
1 = 1 ( 0 ), 2 = 2 ( 0 ) и 3 = 3 ( 0 ): |
|
||||||||
|
|
C |
|
C |
2 |
C2 D2 |
|
|
|
|
arccos |
|
|
|
|
|
|
|
, |
||
1 D2 |
1 D2 |
|||||||||
1 |
|
|
|
1 D2 |
|
|
0 |
|||
|
|
|
|
|
|
|
|
|
|
|
2 |
arccosl0 l1 cos 0 l2 cos 0 1 0 1 , |
|||||||||
|
|
|
|
l2 |
|
|
|
|
|
|

49
3 4π 0 1 2 ,
где |
С |
l2 |
l2 |
l2 l2 |
2l |
l cos |
0 |
, |
|||||
|
0 |
1 |
2 |
3 |
|
|
0 1 |
|
|
||||
|
|
|
2l l |
(cos |
0 |
|
l0 |
) |
|
|
|||
|
|
|
|
|
|
||||||||
|
|
|
|
1 2 |
|
|
|
|
l |
|
|
||
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
D |
sin 0 . |
|||
|
cos |
0 |
l0 |
|
|
|
l |
||
|
|
|
1 |
|
Дифференцированием по углу поворота входного звена 0 получим величины аналогов угловых скоростей и ускорений.
Четырехзвенный механизм структуры 1- 2(2):
Схема кривошипно-ползунного механизма, в составе которого имеется структурная группа 2-го класса 2-го вида (звенья 2 и 3), показана на рис. 2.20.
Y0 |
|
|
Y2 |
X 1 |
|
Y1 |
|
|
|
Y3 |
|
|
1 |
|
|
|
|
|
|
B |
l2 |
|
|
|
l1 |
|
|
||
|
|
2 |
C |
X 3 |
|
|
|
1 |
|||
|
|
|
|||
|
|
|
e |
2 |
|
|
|
0 |
|
||
A |
|
|
|
X 2 |
|
|
|
|
3 |
X 0 |
|
O |
|
|
|
||
|
|
|
xC |
|
|
Рис. 2.20. Кривошипно-ползунный механизм |
|
||||
Входное звено – звено 1. l1 и l2 - размеры звеньев; е – величина
