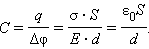10. Электроемкость. Конденсаторы.

Примеры расчета емкости конденсаторов.

• Цилиндрический конденсатор.

• Сферический конденсатор.

Электроемкость — скалярная, физическая величина характеризующая способность проводника или системы проводников накапливать электрический заряд. За величину электроемкости система проводников принимают отношение модуля заряда одного из проводников к разности потенциалов между этим проводником и соседним.       Электрической ёмкостью проводника называется отношение заряда проводника к его потенциалу. В системе СИ единица электроемкости называется фарад (Ф). Существуют такие конфигурации проводников, при которых электрическое поле оказывается сосредоточенным (локализованным) лишь в некоторой области пространства. Такие системы называются конденсаторами, а проводники, составляющие конденсатор, – обкладками. (ток от + к -)

Внутри конденсатора вектора и параллельны; поэтому модуль напряженности суммарного поля равен

Вне пластин вектора и направлены в разные стороны, и поэтому E = 0. Поверхностная плотность σ заряда пластин равна q / S, где q – заряд, а S – площадь каждой пластины. Разность потенциалов Δφ между пластинами в однородном электрическом поле равна Ed, где d – расстояние между пластинами. Из этих соотношений можно получить формулу для электроемкости плоского конденсатора:

Таким образом, электроемкость плоского конденсатора прямо пропорциональна площади пластин (обкладок) и обратно пропорциональна расстоянию между ними. Если пространство между обкладками заполнено диэлектриком, электроемкость конденсатора увеличивается в ε раз:

Сферический конденсатор – это система из двух концентрических проводящих сфер радиусов R₁ и R₂. Цилиндрический конденсатор – система из двух соосных проводящих цилиндров радиусов R₁ и R₂ и длины L.

(сферический конденсатор), 
(цилиндрический конденсатор)

11. Объемная плотность энергии электрического поля. Энергия электрического поля и работа поляризации диэлектрика.

Это физическая величина, численно равная отношению потенциальной энергии поля, заключенной в элементе объема, к этому объему. Для однородного поля объемная плотность энергии равна . Для плоского конденсатора, объем которого Sd, где S - площадь пластин, d - расстояние между пластинами, имеем

С учетом, что и

(16.4)

или

Энергия заряженного конденсатора равна работе внешних сил, которую необходимо затратить, чтобы зарядить конденсатор.

Поляризация диэлектриков — явление, связанное с ограниченным смещением связанных зарядов в диэлектрике или поворотом электрических диполей, обычно под воздействием внешнего электрического поля, иногда под действием других внешних сил или спонтанно.

сли поле однородно (что имеет место в плоском конденсаторе при расстоянии d много меньшем, чем линейные размеры обкладок), то заключенная в нем энергия распределяется в пространстве с постоянной плотностью w. Тогда объемная плотность энергии электрического поля равна

C учетом соотношения можно записать

В изотропном диэлектрике направления векторов D и E совпадают и

Подставим выражение , получим

Первое слагаемое в этом выражении совпадает с плотностью энергии поля в вакууме. Второе слагаемое представляет собой энергию, затрачиваемую на поляризацию диэлектрика. Покажем это на примере неполярного диэлектрика. Поляризация неполярного диэлектрика заключается в том, что заряды, входящие в состав молекул, смещаются из своих положений под действием электрического поля Е. В расчете на единицу объема диэлектрика работа, затрачиваемая на смещение зарядов q_i на величину dr_i, составляет

Выражение в скобках есть дипольный момент единицы объема или поляризованность диэлектрика Р. Следовательно, .

Вектор P связан с вектором E соотношением . Подставив это выражение в формулу для работы, получим

Проведя интегрирование, определим работу, затрачиваемую на поляризацию единицы объема диэлектрика

.