1.4 Методы определения динамической адсорбции

_{В основе расчета процессов очистки и рекуперации, осуществляемых с помощью твердых сорбентов, лежат закономерности динамики адсорбции. Динамика сорбционных процессов рассматривает пространственно-временные распределения компонентов между фазами системы (одна из которых – твердая), возникающие при перемещении этих фаз относительно друг друга [27].}

_{Рассматривается случай модельный случай изотермической адсорбции, не осложненной тепловыми эффектами. Изотерма адсорбции поглощаемого компонента (адсорбтива) имеет выпуклую форму (например, типа изотермы Ленгмюра), которая характерна для мелкопористых адсорбентов [28]. Через слой адсорбента длиной L проходит раствор исходного вещества с адсорбтивом. Концентрацию поглощаемого вещества на входе в слой обозначена как c0. Указанные значения в ходе эксперимента поддерживаются постоянными. Концентрация адсорбата в адсорбенте до начала процесса равна нулю. Оценка изменяется концентрации адсорбтива c(L, t) и его содержание в адсорбированном состоянии a ((L, t) по длине слоя L в зависимости от времени t представлена на рисунке 7.}

_{Рисунок 7 - Схема перемещения фронта адсорбции по слою адсорбента:}

_{В начальный момент времени при t < t0, где t0 – некоторое характерное время, происходит насыщение лобового слоя длиной Lф в нестационарном режиме (позиция 1 на рисунке 7). При t > t0 в слое L > Lф устанавливается стационарный режим с показанным на рисунке. 7 изменением профиля концентраций, который называют фронтом сорбции. В стационарном режиме этот фронт перемещается по длине слоя с постоянной скоростью , где c0 – концентрация на входе; a0 – равновесная этой концентрации величина адсорбции; δ – насыпная плотность адсорбента, ω – линейная скорость, приведенная к диаметру аппарата. На указанной стадии в слое адсорбента можно выделить три характерные зоны: зону работающего слоя L0 (обозначена на рисунке как MTZ), в которой простирается фронт адсорбции и концентрация адсорбтива снижается от c0 до примерно нулевого значения c; зону уже отработавшего слоя, в котором концентрация адсорбтива равна c0, и зону, которая еще не участвует в процессе (еще не работающий слой) [29].}

_{На рисунках 7 и 8 показаны последовательные стадии перемещения фронта сорбции по слою адсорбента. В момент, когда этот фронт достигает конца, концентрация адсорбтива в потоке на выходе из слоя начинает увеличиваться от c ≈ 0 до c0.}

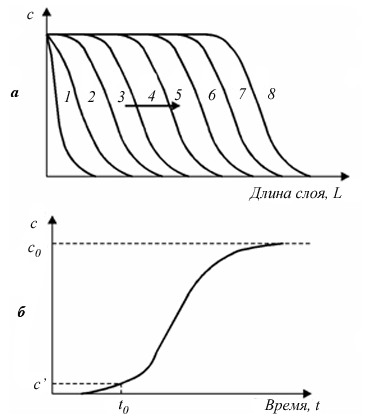
_{Рисунок 8 - Распределение концентраций в различные моменты времени 1 – 8 (а) и изменения концентрации за слоем (б)}

_{График изменений концентрации адсорбтива на выходе из слоя в зависимости от времени t называется выходной кривой или кривой проскока (рисунок 8 б).}

_{Время до появления заданной концентрации адсорбтива c’ за слоем называют временем до проскока или временем защитного действия t(cп) слоя L данного адсорбента до заданного проскока [30]. Реализуемая за время до проскока величина адсорбционной емкости называется динамической емкостью, которая всегда несколько ниже равновесной емкости в статических условиях из-за неполной отработки замыкающего слоя. Зависимость времени защитного действия от длины слоя адсорбента обычно описывается в хорошем приближении уравнением Н.А. Шилова:}

_{, (9)}

_{где , (10)}

_{U – скорость перемещения фронта адсорбции в стационарной области, a0– равновесная этой концентрации величина адсорбции; δ– насыпная плотность адсорбента. Параметр может быть назван временем потери защитного действия, связан с начальным периодом формирования работающего фронта.}

_{В более современной трактовке параметр апроксимируется как}

_{, (11) в результате , (12) или , (13) где (14)}

_{– длина слоя формирования стационарного режима (Lф≈L0); - функция фиксированных значений проскоковых концентраций за слоем [29].}

_{Динамическая адсорбционная емкость поглотителя меньше его равновесной адсорбционной емкости, поскольку в рабочих условиях при непродолжительном контакте твердой и газовой фаз адсорбционное равновесие не может установиться [31].}

_{ад = а∞ η, (15)}

_{где η – степень использования равновесной (статистической) адсорбционной емкости.}

_{При следующих условиях проведения процесса адсорбции Hа = 0,3…0,5 м; w = 0,3…0,5 м/с; С0 = (1…20) · 10}^-3 _кг/м³ _{степень использования равновесной адсорбционной емкости η равна 0,8…0,9. Таким образом, коэффициент запаса – величина, обратная степени использования равновесной адсорбционной емкости} k_з = = , _{равен 1,1...1,2 [32].}

_{Динамическая сорбционная емкость (активность) ад – количество адсорбтива, поглощенного слоем сорбента до момента его появления за слоем (проскока),кг/м}²

_.

_{ад = С0∙w∙τз, (16)}

_{где С0 – начальная концентрация адсорбтива в газовом потоке, кг/м}³_;

_{w – скорость газового потока, м/с;}

_{τз – время защитного действия слоя адсорбента, с. Это время, прошедшее от начала пропускания парогазовой смеси через слой адсорбента до момента появления (проскока) адсорбтива за слоем адсорбента [33].}

_.