5. Линейные и квадратичные формы. Дифференцирование матриц и функций от векторов по скалярным и векторнЫм переменным

Определение 5.1 (О5.1). Пусть каждому вектору линейного действительного пространстваставится в соответствие вполне определенное число из. Тогда говорят, что в линейном пространстве определенаскалярная функция от вектора .

Определение 5.2 (О5.2). Функция , областью определения которой является линейное пространство , а областью значений – совокупность действительных чиселR, называется действительной линейной формой (линейным функционалом), если выполняется соотношение

(5.1)

для любых векторов ии любых действительных чисели.

Пусть – естественный базис в пространстве,– вектор-столбец координат векторав этом базисе, тогда любая линейная форма может быть представлена в следующем виде:

, (5.2)

где . Наоборот, при любых действительных числах выражение (5.2) определяет некоторую линейную форму в .

Определение 5.3 (О5.3). Множество всех векторов , для которых , называется ядром линейной формы (функционала) и обозначается :

. (5.3)

Линейную форму (5.2) можно записать в как скалярное произведение

, (5.4)

где .

Определение 5.4 (О5.4). Пусть – некоторое подпространство пространства. Выберем впроизвольный векторu, тогда множество векторов z=u+v, где vL, называют плоскостью в пространстве . Векторu называется вектором сдвига, а подпространство L – направляющим подпространством этой плоскости.

Определение 5.5 (О.5). Гиперплоскостью H в пространстве называется плоскость размерностьюn–1. Если L^ – ортогональное дополнение направляющего подпространства L гиперплоскости H и N – любой его базисный вектор, то уравнение гиперплоскости можно записать в следующем виде:

, (5.5)

где вектор NL^ есть нормаль к гиперплоскости H, b – действительное число.

Определение 5.6 (О5.6). Квадратичной формой от n действительных переменных называется функция вида

, (5.6)

где – действительные числа.

Если составить симметричную матрицу A из коэффициентов , называемую матрицей квадратичной формы, и рассматривать величиныкак координаты векторав некотором ортонормированном базисе (например, естественном), то квадратичная форма может быть записана какскалярное произведение или квадрат евклидовой векторной нормы с весом :

(5.7)

Рангом квадратичной формы называется ранг ее матрицы. При замене переменныхформастановиться квадратичной формойновых переменных, причем матрицаэтой форме связана с матрицейсоотношением

, (5.8)

при этом если матрица неособенная, то ранг квадратичной формыне меняется.

Любую квадратичную форму рангаможно неособым линейным преобразованием привести кканоническому виду.

, (5.9)

где – все отличные от нуля числа. Канонический вид называетсянормальным видом, если все коэффициенты в (5.9) равны 1 или –1. Число положительных коэффициентов в выражении (5.9) называется положительным индексом инерции, число отрицательных коэффициентов – отрицательным индексом инерции, а разность между ними – сигнатурой квадратичной формы.

Симметричная матрица A квадратичной формы имеет ортонормированную систему собственных векторов в евклидовом пространстве , соответствующих собственным значениямматрицы, которые все являются действительными числами. Поэтому матрицаквадратичной формыортогонально подобна матрице с действительными собственными значениями матрицы :

, (5.10)

где – ортогональная матрица, составленная из столбцов координат ортонормированных собственных векторов матрицыв том же базисе, в котором задана.

Определение 5.7 (О5.7). Квадратичная форма называетсяположительно определенной, если при, инеотрицательно определенной если при любых. Аналогично определяютсяотрицательно определенная и неположительно определенная квадратичные формы. Если форма принимает разные знаки при некоторых, то она называетсянеопределенной. Для того, чтобы квадратичная форма была положительно определенной, необходимо и достаточно, чтобы все главные миноры матрицы этой формы были положительны (критерий Сильвестра).

Пусть– собственные значения положительно определенной матрицы, тогда для всех векторовсправедливы неравенства

. (5.11)

Определение 5.8 (О5.8). Если все собственные значения матрицы квадратичной формы имеют одинаковый знак, то форма называется эллиптической, а уравнение , где, определяет в пространствегиперэллипсоид постоянного значения (уровня).

Рассмотрим основные правила дифференцирования функций от векторов и матриц по скалярным и векторным переменным.

1. Пусть – матрица, элементы которой суть функциискалярной переменной.Тогда производнойот матрицыпоявляется матрица, составленная из производныхее элементов по переменной, что может быть записано в форме

.

Для производной от суммы и произведения матриц, зависящих от скалярной переменной по этой переменной справедливы представления

Для степенной матричной функции от квадратной– матрицы, где– целое положительное число, производная по скалярной переменнойвычисляется в силу соотношения

.

Примечание 5.1 (ПР5.1). Если , то.

Для вычисления производной от обратной матрицы сформулируем и докажем следующее утверждение.

Утверждение 5.1 (У5.1). Производная от обратной матрицыпо скалярной переменнойвычисляется по формуле

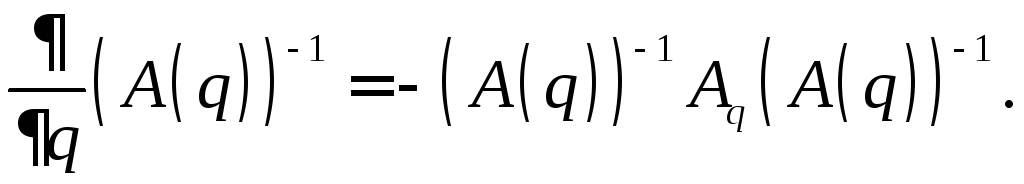□(5.12)

Доказательство утверждения строится на дифференцировании по скалярному параметру матричного уравнения, где– единичная матрица, в результате которого получим

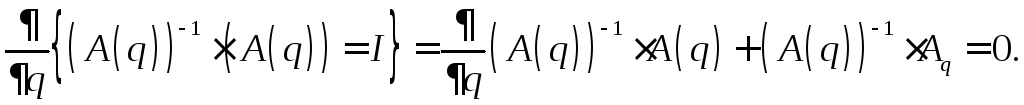
Разрешение полученного матричного уравнения относительно производной приводит к (5.12). ■

2. Пусть –скалярная функция векторного аргумента . Тогда, обозначив символомоператор градиента, дляпроизводной от этой функции по векторному аргументу и градиента можно записать следующие представления:

–вектор–столбец;

–вектор–строка;

––матрица.

3. Пусть – вектор–столбец скалярных функций отвектора (векторная функция от векторного аргумента), тогда

. (5.13)

– матрица размерами . Аналогично определяется производная

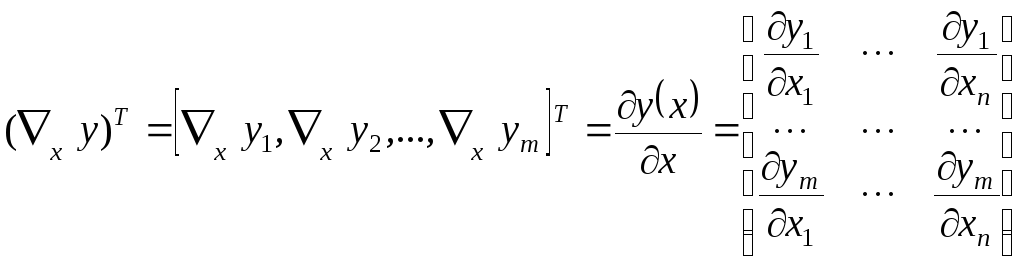. (5.14)

4. Пусть и– векторы–столбцы размерности, и– вектор-столбец размерности. Тогда производная поот скалярного произведения векторови(градиент скалярного произведения) определяется следующим образом:

. (5.15)

Решение вариантов задач

Задача 5.1. Записать квадратичную форму с симметричной матрицей этой формы.

Решение 1. Запишем квадратичную форму в форме, в результате для матрицыполучаем представление

Решение 2. Матрица исходной формыимеет вид. Любая действительная матрица может быть представлена в виде:, где– симметричная матрица,– кососимметричная матрица. Поскольку для любого вектора, то, поэтому имеем, гдев данном случае равна.

Задача 5.2. Привести матрицу квадратичной формы ортогональным преобразованиемк каноническому виду.

Решение. Матрица есть матрица собственных векторов единичной нормы. Вычисление корней характеристического уравнениядает следующие собственные значения матрицыквадратичной формы:.

Решив систему уравнений , получим два ортонормированных собственных вектора, соответствующих собственному значению:.

Решив систему уравнений для, получим третий вектор ортонормированной системы, соответствующий этому собственному значению:. В итоге матрица ортогонального преобразованияпринимает вид

.

Матрица канонического вида формы равна так, что, при этом.

Задача 5.3. Вычислить производные от следующих скалярных функций от вектора

а) ; б); в).

Решение. По определению производной получим для случаев:

а) ; б)в)

69