
- •Министерство образования и науки Российской Федерации
- •Предисловие
- •Используемые обозначения и сокращения
- •Введение. Основные проблемы управления
- •Часть 1. Векторно-матричный формализм метода пространства состояний
- •1. Алгебраические структуры
- •Пространства
- •2.1. Метрические пространства. Примеры метрик
- •2.2. Линейные пространства и операторы. Матрицы линейных
- •3. Матричные инварианты и неинварианты. Сингулярное разложение матриц
- •4. Канонические формы матриц. Матрицы приведения подобия
- •5. Линейные и квадратичные формы. Дифференцирование матриц и функций от векторов по скалярным и векторнЫм переменным
Часть 1. Векторно-матричный формализм метода пространства состояний
1. Алгебраические структуры
Для изучения основных разделов современной теории управления, опирающейся на векторно-матричный формализм метода пространства состояний (МПС), необходимо определенное знакомство c алгебраическими структурами и пространствами. Схема их формирования, взаимной связи и изучения приведена на рисунке 1.1.

Рисунок 1.1
Определение
1.1 (О1.1).
Множеством
называется совокупность объектов любой
природы, задаваемая путем их перечисления
или указанием их характеристического
свойства
![]() :
:
![]() .
.
Последняя
запись означает, что множество
![]() есть совокупность элементов
есть совокупность элементов![]() ,
обладающих характеристическим свойством
,
обладающих характеристическим свойством![]() .
.
Мощность
множества
![]() характеризует число элементов множества
и обозначается
характеризует число элементов множества
и обозначается![]() .
.
Определение
1.2 (О1.2).
Пусть задано множество
![]() ,
будем говорить, что во множестве
,
будем говорить, что во множестве![]() определена бинарная алгебраическая
операция, если указано правило, по
которому любой паре элементов
определена бинарная алгебраическая
операция, если указано правило, по
которому любой паре элементов![]() из этого множества, взятых в определенном
порядке ставится в соответствие
единственный элемент
из этого множества, взятых в определенном
порядке ставится в соответствие
единственный элемент![]() того же множества.
того же множества.
Определение 1.3 (О1.3). Алгебраической структурой называется множество с заданными в нем алгебраической бинарной операцией (или несколькими операциями) и свойствами элементов относительно этой бинарной операции.
Ниже изучаются следующие алгебраические структуры: группа (подгруппа), кольцо, идеал, поле, простое и расширенное поля Галуа.
Определение
1.4 (О1.4).
Множество
![]() называютсягруппой,
если для любой пары элементов множества
называютсягруппой,
если для любой пары элементов множества
![]() определена бинарная алгебраическая
операция
определена бинарная алгебраическая
операция![]() и выполняются условия:
и выполняются условия:
Замкнутости: для
 ,
элемент
,
элемент ;
;Ассоциативности: для

 ;
;Существования нейтрального элемента (единицы группы): G содержит единственный элемент

Существования обратного элемента: для
 (единственный для
(единственный для ),
называемый элементом, обратным
),
называемый элементом, обратным ,
такой, что
,
такой, что .
.
Примечание
1.1 (П1.1):
Группа
![]() называетсякоммутативной
или абелевой группой, если выполняется
условие коммутативности: для
называетсякоммутативной
или абелевой группой, если выполняется
условие коммутативности: для
![]() .
.
Определение
1.5 (О1.5). Подмножество
![]() группы
группы![]() называетсяподгруппой,
если оно удовлетворяет всем свойствам
группы относительно бинарной алгебраической
операции *.
называетсяподгруппой,
если оно удовлетворяет всем свойствам
группы относительно бинарной алгебраической
операции *.
Определение
1.6 (О1.6).
Пусть
![]() коммутативная группа,
коммутативная группа,![]() подгруппа группы
подгруппа группы![]() .
Рассмотрим множество
.
Рассмотрим множество

где
![]() .
.
Определенные
таким образом множества называются
смежными классами группы
![]() по подгруппе
по подгруппе![]() и задают разложение группы
и задают разложение группы![]() по подгруппе
по подгруппе![]() с образующими элементамиβi,
так что
с образующими элементамиβi,
так что
![]() .
Число
.
Число![]() называется индексом подгруппы
называется индексом подгруппы![]() в группе
в группе![]() .
.
Определение
1.7 (О1.7). Пусть
имеются две группы
![]() и
и![]() с бинарными операциями «
с бинарными операциями «![]() »
и «
»
и «![]() »
соответственно одной и той же мощности
и
»
соответственно одной и той же мощности
и![]() отображение
отображение![]() в
в![]() такое, что для всех
такое, что для всех![]() имеет место равенство:
имеет место равенство:![]() .
.
Отображение
![]() ,
обладающее таким свойством, называетсяизоморфным.
Если между двумя группами
,
обладающее таким свойством, называетсяизоморфным.
Если между двумя группами
![]() и
и![]() можно
установить изоморфизм
можно
установить изоморфизм![]() ,
то группы
,
то группы![]() и
и![]() называютсяизоморфными.
называютсяизоморфными.
Определение 1.8 (О1.8). Множество R называется кольцом, если на нем определены бинарные алгебраические операции сложения и умножения и выполняются следующие условия:
Множество R является коммутативной группой относительно бинарной операции сложения;
Замкнутости относительно бинарной операции умножения: для
 R
элемент
R
элемент
 R;
R;Ассоциативности относительно бинарной операции умножения: для
 R
R
 ;
;Дистрибутивности относительно бинарных операций сложения и умножения: для
 R
R

 .
.
Примечание
1.2 (П1.2).
Кольцо R
называется коммутативным,
если выполняется условие:
![]() R
R
![]() .
.
Определение
1.9 (О1.9).
Подгруппа J
аддитивной группы
R
называется
идеалом,
если для
![]() R
и
R
и
![]() элемент
элемент![]() .
.
Примечание
1.3 (П1.3). Идеал,
состоящий из всех элементов, кратных
некоторому элементу
![]() кольцаR,
называется главным
идеалом. Кольцо, в котором каждый идеал
главный, называется кольцом
главных идеалов.
Элемент
кольцаR,
называется главным
идеалом. Кольцо, в котором каждый идеал
главный, называется кольцом
главных идеалов.
Элемент
![]() называетсяобразующим
(или порождающим)
элементом идеала.
называетсяобразующим
(или порождающим)
элементом идеала.
Поскольку
для кольца R
справедливы все свойства группы, а для
идеала
![]() все свойства подгруппы относительно
бинарной операции сложения, то кольцоR
можно разложить подобно группе на
смежные классы по идеалу
все свойства подгруппы относительно
бинарной операции сложения, то кольцоR
можно разложить подобно группе на
смежные классы по идеалу
![]() .
.
Определение
1.10 (О1.10). Коммутативное
кольцо
![]() называетсяполем,
если выполняются следующие условия:
называетсяполем,
если выполняются следующие условия:
Кольцо
 содержит нейтральный элемент 1
относительно бинарной операции умножения
такой, что для
содержит нейтральный элемент 1
относительно бинарной операции умножения
такой, что для
 ;
;Для
 ,
, существует обратный элемент
существует обратный элемент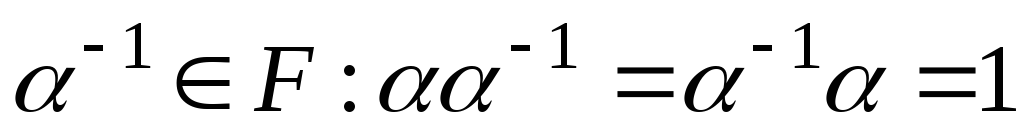 ;
;Если
 то
то или
или
Определение
1.11 (О1.11).
Если
![]() – простое число, то кольцо чисел по
модулюp
(
– простое число, то кольцо чисел по
модулюp
(
![]() )
называетсяпростым
полем Галуа
и обозначается
)
называетсяпростым
полем Галуа
и обозначается
![]() .
.![]() состоит из элементов
состоит из элементов![]() ,
таким образом
,
таким образом![]() .
.
Примечание
1.4 (П1.4). Определим
на множестве
![]() две бинарные операции – сложения по
две бинарные операции – сложения по![]() ,
обозначив его
,
обозначив его![]() ,
и умножения по
,
и умножения по![]() ,
обозначив его
,
обозначив его![]() :
:
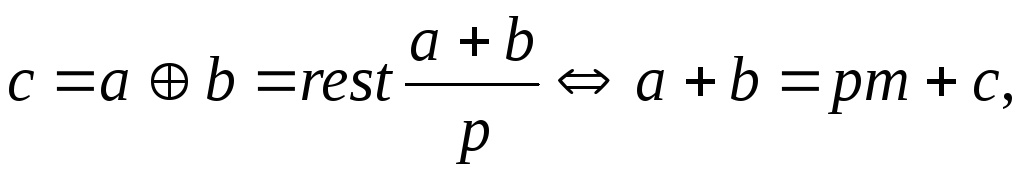 где
где
 – целое;
– целое; ,
где
,
где
 – целое.
– целое.
При
этом
![]() и
и![]() называютсявычетами.
называютсявычетами.
Определим
понятия сравнимости по
![]() .
Два целых числа
.
Два целых числа![]() и
и![]() сравнимы по
сравнимы по![]() :
:
![]() где
где
![]() –
целое.
–
целое.
Определение
1.12 (О1.12).
Полином
![]() называетсяполиномом
над полем
называетсяполиномом
над полем
![]() или модулярным,
если его коэффициенты
или модулярным,
если его коэффициенты
![]() принадлежат простому полю
принадлежат простому полю![]() .Степенью
полинома
.Степенью
полинома
![]()
![]() называется наибольшее число
называется наибольшее число![]() .
.
Примечание
1.5 (П1.5).
Сравнение модулярных полиномов
![]() и
и![]() по модулю модулярного полинома
по модулю модулярного полинома![]() ,
производится аналогично сравнению
целых чисел по
,
производится аналогично сравнению
целых чисел по![]()
![]() ,
,
где
![]()
![]() .
.
Аналогично
можно ввести операции суммирования
(вычитания), умножения по модулю
модулярного полинома, при этом приведение
подобных членов производится по
![]() .
Так,
.
Так,
![]() ,
,
где
![]() .
При этом
.
При этом![]() называетсявычетом
по
называетсявычетом
по
![]() .
.
Определение
1.13 (О1.13)
Полная система вычетов по двойному
модулю
![]() образует конечное поле, содержащее
образует конечное поле, содержащее![]() элементов, которое обозначается
элементов, которое обозначается![]() и называетсярасширенным
полем Галуа.
и называетсярасширенным
полем Галуа.
В
отличие от простого поля
![]() элементами расширенного поля
элементами расширенного поля![]() являются уже не числа, а модулярные
полиномы степени не выше
являются уже не числа, а модулярные
полиномы степени не выше![]() с коэффициентами из простого поля
с коэффициентами из простого поля![]() .
.
Решения вариантов задач.
Задача 1.1. Определить, относительно какой бинарной операции – умножения или сложения – следующие числовые множества образует группу, или не образует ее вовсе:
а)
Множество всех вещественных чисел
![]() .
.
б) Множество вещественных чисел отличных от нуля.
в) Множество положительных вещественных чисел.
г) Множество всех комплексных чисел.
д) Множество комплексных чисел, отличных от нуля.
е) Множество комплексных чисел с модулем равным единице.
ж) Множество комплексных чисел с модулем большем единицы.
з)
Множество чисел, представляющих собой
целые положитель-
ные степени
числа 2
![]() .
.
и)
Полное множество чисел
![]() ,
где
,
где![]() .
.
Решение.
В
соответствие с определением группы
![]() при заданной бинарной операции необходимо
выполнение условий аксиом:
при заданной бинарной операции необходимо
выполнение условий аксиом:
замкнутости;
ассоциативности;
существования нейтрального элемента (единицы группы;
существования обратного элемента.
Тогда имеем в вариантах задачи:
а) Группу относительно сложения и умножения. Действительно:
![]()
![]()
нейтральный элемент
 относительно сложения и
относительно сложения и относительно умножения;
относительно умножения;обратный элемент

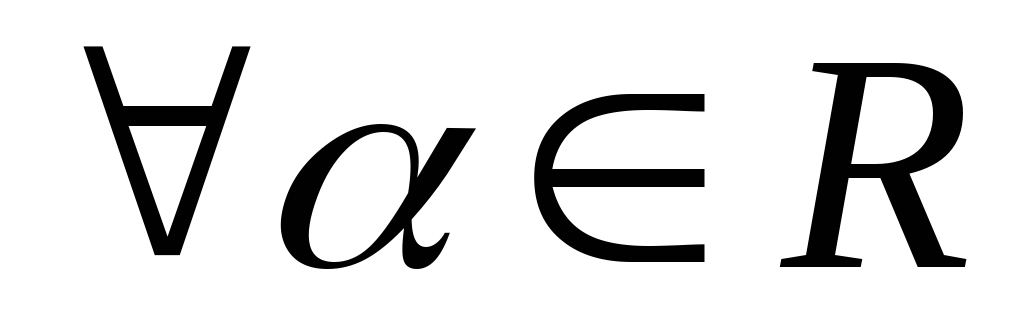
 относительно сложения
относительно сложения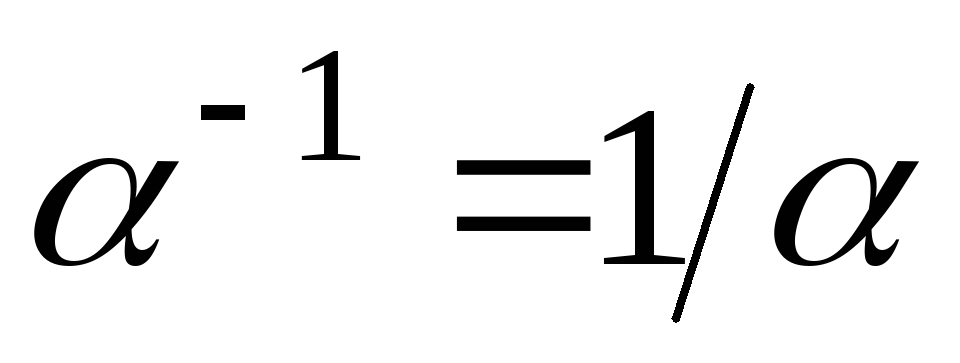 относительно умножения, при этом
относительно умножения, при этом
б) Группу относительно умножения
в) Группу относительно умножения
г)
Группу относительно сложения и умножения.
Действительно:
![]() где
где![]() – множество комплексных чисел
воспользуемся декартовой и полярной
формами представления чисел, так, что
– множество комплексных чисел
воспользуемся декартовой и полярной
формами представления чисел, так, что

нейтральный элемент
 относительно сложения и
относительно сложения и относительно умножения:
относительно умножения:обратный элемент
 равен:
равен: относительно сложения и
относительно сложения и относительно умножения;
относительно умножения;
д) Группу относительно умножения
е) Группу относительно умножения
ж) Не образует группы ни относительно сложения, ни относительно умножения, так как не содержит единиц группы.
з)
Не образует группы в обоих случаях, так
как относительно сложений не включаются
условия замкнутости, относительно
умножения не существует
![]() ;
;
и) Образует группы относительно умножения.
Задача 1.2. Выяснить, образуют ли кольцо следующие множества:
а) Множество четных чисел;
б) Множество нечетных чисел;
в) Множество рациональных чисел;
г) Множество вещественных чисел;
д) Множество комплексных чисел;
е)
Множество целых чисел, кратных данному
целому числу большему
![]() ;
;
ж)
Множество чисел вида
![]() ,
где
,
где![]() и
и![]() целые.
целые.
Решение. В соответствии с определением 1.8 кольца R на элементах кольца должны быть заданы бинарные операции сложения и умножения и выполняться условия (аксиомы):
коммутативности R как группы относительно сложения
замкнутости относительно умножения
ассоциативности относительно умножения
дистрибутивности.
Тогда имеем в вариантах задачи:
а)
Образует кольцо. Действительно, множество
четных чисел
![]() образует коммутативную группу относительно
сложения
образует коммутативную группу относительно
сложения
![]()
![]()
![]()
б) Не образует кольцо, так как не выполняются групповые свойства множества нечетных чисел
в) Образуют кольцо.
г) Образуют кольцо.
д) Образуют кольцо.
е)
Если считать, что ноль кратен целому
числу
![]() ,
то это множество образует кольцо.
,
то это множество образует кольцо.
ж)
Не образует кольцо, так как не выполняются
условия замкнутости по умножению.
Действительно, пусть
![]()
![]() где
где![]() целые, тогда
целые, тогда![]() ,
где
,
где![]() перестает быть целым.
перестает быть целым.
Задача 1.3. Выяснить, какие из множеств задачи 1.2 образуют поле.
Решение.
Напомним, что для того чтобы кольцо R
образовывало поле
![]() необходимо выполнение следующих условий:
необходимо выполнение следующих условий:
коммутативности кольца,
существования единиц
 ,
, ,
,существования обратного элемента

 .
.
Тогда поля будут образовывать в задаче 1.2 множества в), д), е).
