2. Пространства

Определение 2.1 (О2.1). Пространством называется множество объектов математической природы (точка, кривая, вектор, матрица, геометрическая фигура, многообразие и т.д.), именуемых элементами пространства, на которых заданы геометрические характеристики, определяющие расстояние между элементами, их размер, взаимное положение и т.д.

2.1. Метрические пространства. Примеры метрик

Определение 2.2 (О2.2). Пусть произвольные элементы x и y множества образуют пару, тогда отображение

(2.1)

во множество действительных чисел , называетсяметрикой и обозначается , если оно удовлетворяет:

1. условию неотрицательности

2. условию симметрии

3. условию неравенства «треугольника»

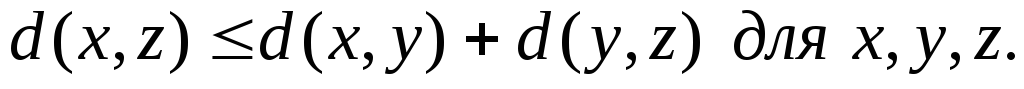
Содержательно метрика представляет собой вещественнозначную положительную величину, определяющую расстояние между элементами или степень различия элементов множества .

Определение 2.3 (О2.3). Множество с введенной в нем метрикойобразуетметрическое пространство (МП), обозначаемое в одной из форм

Примечание 2.1 (П2.1). Так как на элементах множества может быть задано бесконечное число метрик, то на нем может быть построено бесконечное число метрических пространств

Рассмотрим примеры метрик и метрических пространств.

Если – множество действительных чисел, тообразует метрическое пространствос метрикой

(2.2)

Эта метрика именуется обычной (простой) или абсолютной на .

Если , то есть оно образовано–элементными числовыми массивами (именуемыми также–ками,–кортежами,–векторами), представляемыми в виде

то на множестве может быть задана обобщенная гёльдеровская векторная метрика, определяемая выражением

(2.3)

где p – целое положительное число. Наиболее употребительными векторными метриками являются:

2.1. абсолютная векторная метрика при

; (2.4)

2.2. квадратичная векторная метрика при

; (2.5)

2.3. экстремальная метрика при

(2.6)

3. Если множество образовано-ками видагде элементыпринадлежат простому полю Галуа, то-кииименуются кодами или кодовыми векторами, при этом на множествеможет быть построена метрика Ли

(2.7)

Если так, что, то метрика Ли вырождается в метрикуХэмминга

(2.8)

где – знак операции суммирования по модулю два (). Содержательно метрика Хэмминга определяет число разрядов кодовых векторови, в которых эти векторы отличаются друг от друга. МетрикаХэмминга именуется такжекодовым расстоянием.

4. Если множество образовано множеством вещественнозначных функций времении, заданных на интервале, то на множествеможет быть задана-ичная функциональная метрика, определяемая интегральным выражением

. (2.9)

Наиболее употребительными функциональными метриками являются:

4.1. абсолютная функциональная метрика при

; (2.10)

4.2. квадратичная функциональная метрика при

; (2.11)

4.3. экстремальная функциональная метрика при

. (2.12)

Определение 2.4 (О2.4). Метрическое пространство называетсясепарабельным, если для любого существует счетная последовательностьэлементов множестватаких, чтодля некоторогои любогоX.

Определение 2.5 (О2.5). Метрическое пространство называетсякомпактным, если можно найти конечную последовательность элементов множестватаких, чтодля некоторогои любого элемента.

Решение вариантов задач

Задача 2.1.Вычислить векторную метрику Ли для векторов, элементы которых принадлежат простому полю Галуа.

Решение. В силу определения (2.7) метрики Ли можно записать

Ответ:

Задача 2.2. Вычислить векторную метрику для векторовдля значений

Решение. В силу определения (2.4), (2.5), (2.6) метрики для значенийполучим: