5 курс / евстрапов / 0364109_90FD6_evstrapov_a_a_nanotehnologii_v_ekologii_i_medicine_kurs_lekc

А.А. Евстрапов. Курс лекций «Нанотехнологии в экологии и медицине»

порядка 1000 (в некоторых работах принято ~2450). Кроме того, кинематическая вязкость ν = ηρ имеет порядок 10-2 см2/сек.

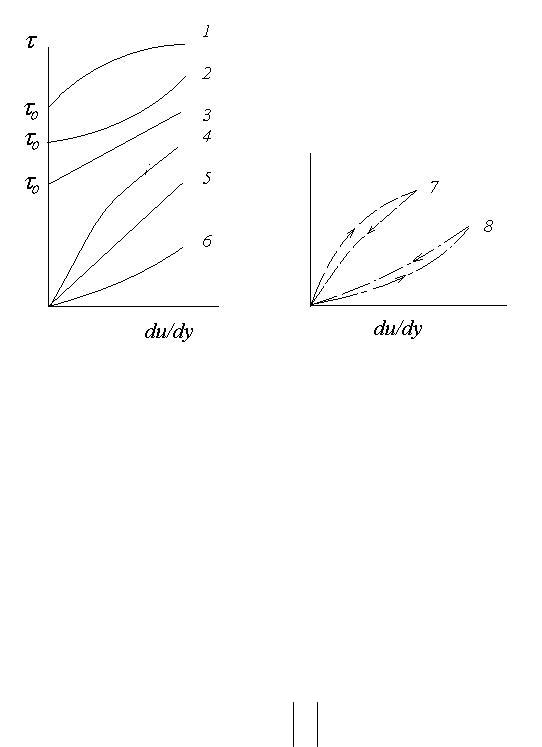
Рисунок 3.1.4. Зависимость касательного напряжения от скорости сдвига для жидкостей: а – жидкости с независящими от времени свойствами 1, 2 – жидкости с пределом текучести и нелинейной кривой течения, 3 – пластическая жидкость Бингама, 4 – псевдопластическая жидкость (с разрежением сдвига), 5 – ньютоновская жидкость,

6 – дилатантная жидкость (со сгущением сдвига). Б – жидкости с зависящими от времени свойствами: 7 – тиксотропная жидкость, 8 - реопектическая жидкость.

Удобной реологической моделью для жидкостей, не имеющих предельного напряжения сдвига и с независящими от времени свойствами является модель степенной жидкости Оствальдаде Вилля (Оствальда), хорошо зарекомендовавшая себя на практике. Она характеризуется эмпирическими параметрами: m (консистентность смеси или коэффициент совместимости) и N (параметр неньютоновости или показатель степени жидкости). N характеризует отклонение от ньютоновской жидкости (вода, N =1): для дилатантных жидкостей (концентрированной суспензии) N >1, а для псевдопластичных жидкостей (полимеров) N<1. При таком подходе связь между касательными напряжениями τ в среде и скоростью

конвективного движения имеет вид: τ m ∂u ∂u N −1 .

∂z ∂z

Вязкость жидких сред во многом определяет режимы их течения и возникающие при этом сопротивления, что играет важную роль при лабораторных исследованиях проточных систем, при экспресс-анализе и динамических измерениях.

21

А.А. Евстрапов. Курс лекций «Нанотехнологии в экологии и медицине»

Для количественной оценки режимов движения широко используют различные безразмерные характеристики, например число Рейнольдса, о котором будет изложено в разделе 3.3.

3.1.5. Межфазовые взаимодействия

Большое значение в микрофлюидике имеют межфазовые взаимодействия жидких сред с твердыми материалами и газами (граничное натяжение, возникновение граничных слоев, электрокапиллярные, электрокинетические и другие поверхностные явления). Под действием поверхностных сил поверхности раздела между фазами стремятся к минимуму площади. Для характеристики этого явления вводится величина поверхностного натяжения σ, которая определяется работой, затрачиваемой на изотермический обратимый процесс образования единицы площади поверхности раздела двух равновесных фаз. Поверхностные (граничные) натяжения на границах жидкость-газ, как правило, бывает больше, чем на границах жидкость-жидкость. В случае многокомпонентных систем, когда возможна адсорбция компонентов Гk на межфазной границе, поверхностное натяжение определяется уравнением Гиббса:

ν−1

σ=ϕ − ∑μk Γk ,

k

где ϕ - свободная удельная поверхностная энергия, μk - химические потенциалы компонентов, k – номер границы между компонентами.

Избыток поверхностной энергии, повышенная активность молекул и различные межфазные физико-химические взаимодействия в поверхностном слое приводят к возникновению разнообразных поверхностных явлений. Тенденцией многофазных систем к уменьшению их поверхностной энергии объясняются капиллярные явления, диспергирование, коалесценция (слияние) капелек или пузырьков в эмульсиях и пенах, коагуляция частиц дисперсной фазы в суспензиях, различные виды адсорбции, приводящей к изменению химического состава поверхностного слоя, и др.

3.2.Моделирование в микро- и нанофлюидике (совместно с доктором физ-мат.

наук Буляницей А.Л.).

При моделировании процессов в микроразмерных системах основополагающим являются следующие базовые принципы:

1)гипотеза ламинарности потоков (иногда, ее полагают само собой разумеющейся, если речь идет о микрофлюидике),

2)гипотеза сплошной среды (выявление границ применимости),

3)законы формирования скоростного профиля, массопереноса, распределение электрического и теплового полей,

4)граничные условия, связанные с геометрией элементов конструкций (стенки каналов, зоны смесителей потоков и т.д.).

Поскольку рассматриваются физико-химические процессы переноса вещества и энергии, математические модели, в большинстве своем, имеют форму систем дифференциальных уравнений второго порядка в частных производных. Методы решения таких уравнений — аналитические (Фурье и его модификации, например, метод Гринберга, Галеркина, в ряде случаев, метод Даламбера и функций Грина, операторный метод Лапласа и т.д.) или численные (явные или, что более эффективно, неявные конечно-разностные схемы) — традиционны. Развитие затрагивает, в

22

А.А. Евстрапов. Курс лекций «Нанотехнологии в экологии и медицине»

основном, численные методы и идет по пути экономии использования вычислительных ресурсов и увеличения быстродействия современной вычислительной техники.

Ламинарность потока.

Ламинарный поток - состояние, в котором скорость частицы в жидком потоке - не случайная функция времени. Малые размеры микроканалов (характерные размеры от 5 до 300 мкм) и низкая шероховатость поверхности создают хорошие условия для создания ламинарного потока. Традиционно представление о характере потока дают безразмерные характеристические числа: число Рейнольдса и фактор трения Дарси. При движении жидкостей в каналах достаточно редко достигается турбулентный режим. В то же время, движение газов, как правило, турбулентное.

3.2.1. Подобие гидродинамических явлений. Характеристические числа.

При изучении сложных физико-химических процессов, например, массоперенос вещества в микроканалах при реализации сепарационных методов анализа, можно использовать т.н. теорию подобия гидродинамических явлений. В частности, это дает возможность изучения (в т.ч. методами имитационного моделирования) модельных аналогов исходной конструкции микроканала и режима (условий) анализа. Требуется равенство некоторых характеристических чисел исходного (реального) и модельного объектов. В этом случае найденные для модели закономерности обоснованно переносятся на реальный объект.

К основным характеристическим числам, связанным с процессами конвективнодиффузионного массо- и теплопереноса смесей химических и биологических веществ в микроканалах следует отнести: число Рейнольдса, число Пекле, число Фурье, число

Прандтля (Шмидта), число Боденштейна, число Кнудсена и ряд других.

Одним из базовых безразмерных параметров теории подобия является число Рейнольдса (Re), которое позволяет характеризовать поток как ламинарный (безвихревой) или турбулентный. Следует заметить, что положение о ламинарности конвективного потока вещества – ключевое для определения микрофлюидики.

значение линейной (конвективной) скорости, dc – характерный размер системы, η – динамический коэффициент вязкости (кг/мHс).

При достижении Re некоторого критического значения, поток становится турбулентным. В некоторых источниках переход от ламинарного к турбулентному режиму описывается более сложной схемой: при достижении первого критического числа происходит потеря ламинарности и наступление переходного режима, а при превышении второго критического значения поток становится турбулентным.

Рассмотрим оценки первого критического числа Рейнольдса.

А) понятие характерной скорости допускает различные толкования – средняя по сечению, максимальная, скорость на уровне толщины вытеснения (или на уровне толщины потери импульса) и т.д. Естественно, что разные варианты скорости приводят к различным оценкам критического значения числа Рейнольдса. В подавляющем большинстве случаев используется среднее значение скорости.

Б) характерный размер объекта – также по-разному трактуемое понятие. В реальных объектах следует брать, по крайней мере, два характерных размера: характерная длина (например, рабочая длина канала) и характерный размер сечения. Соответственно чисел Рейнольдса, как характеристик объекта, будет два: продольное и поперечное.

23

А.А. Евстрапов. Курс лекций «Нанотехнологии в экологии и медицине»

Понятие характерный размер сечения нуждается в пояснении. В случае круглого сечения этим размером может быть диаметр, для плоской щели размер связан с ее шириной, для коаксиала размер связан с шириной зазора и т.п.

Вводится общее понятие – гидравлический (гидродинамический) диаметр сечения,

определяемый как dc = 4PS . Здесь S и Р — площадь и периметр сечения

сепарационного канала. Нетрудно убедиться в том, что в простейших случаях сечений гидродинамический диаметр совпадает с естественно выбираемым характерным размером. Например, в случае круглого сечения gd=2r (диаметр круглого канала), плоской щели gd=2δ (удвоенная высота щели), коаксиального капилляра gd=2(r2-r1), прямоугольного сечения gd=2ab/(a+b) (гармоническое среднее ширины и высоты сечения), равностороннего треугольника gd=2ml/3, где ml — медиана (т.е. совпадает с расстоянием от вершин треугольника до его центра тяжести).

Приведем критические значения чисел Рейнольдса для некоторых систем:

•для цилиндрической трубы – от 300 до 3000 (наиболее распространенные оценки

2000-2200),

•для коаксиального капилляра – от 2000 до 7700 (при этом характерный размер во всех случаях – гидравлический диаметр сечения),

•при обтекании плоской пластины (по существу, при поиске продольного критического числа Рейнольдса) приведены оценки от 50000 до 300000,

•для плоской щели – от 1000 до 7000 (характерный размер – ширина щели),

•для прямоугольной трубы в зависимости от соотношения сторон, приведены оценки от 800 до 1400 при характерном размере – наименьшей из сторон прямоугольника. Следует обратить внимание на весьма существенное расхождение представленных эмпирических оценок.

При реализации электрофореза (и других сепарационных методов) на микрочипе

вжидкой среде, поперечные характеристические числа, как правила, не превосходят 0.1, продольные – 10-100. Таким образом в большинстве случаев условие ламинарности выполнено.

Превышение критических чисел Рейнольдса возможно для некоторых случаев использования газообразной среды разделения.

Фактор трения Дарси соотносит эффекты трения и давление в канале:

Число Фурье τ0 — это отношение времени миграции неудерживаемого вещества из капилляра t0 ко времени диффузии молекулы от стенки к стенке капилляра dc2/Dm

(т.е. среднее число столкновений со стенкой за время движения в капилляре). Можно выразить t0 = L / u , и тогда число Фурье для процесса массопереноса выразится

причем, α - коэффициент молекулярной температуропроводно-сти, t0 – постоянная времени переходных процессов.

24

А.А. Евстрапов. Курс лекций «Нанотехнологии в экологии и медицине»

определяет характер жидкости. Принято считать, что для водоподобных жидкостей это число порядка 1000. Число Прандтля – аналог числа Шмидта с учетом замены коэффициента диффузии на коэффициент температуропроводности.

Число Пекле традиционно определяют как Pe = Re/ Sc . То есть, число Пекле

— это средняя линейная скорость u, деленная на скорость ортогональной потоку диффузии Dm/dc, то есть, отношение объемного движения к радиальному массопереносу. Очевидно, что это число должно характеризовать степень размывания электрофоретических пиков компонент анализируемых смесей.

В качестве меры подобия профиля скорости и концентрации в процессах массопередачи применяют диффузионное число Прандтля:

Pr = PeRe = ρηD .

Число Боденштейна характеризует влияние продольного перемешивания на градиенты концентрации веществ в потоке. По форме аналогично числу Рейнольдса с заменой коэффициента кинематической вязкости (отношение ρ/ηm) на коэффициент продольной диффузии Dm.

Число Фруда Fr есть мера отношения сил инерции и тяжести. По-существу, определяет необходимость учета сил тяжести при анализе движения вещества. В явном виде Fr=u2/(gdc), где g – ускорение свободного падения. (Чем больше величина Fr, тем менее существенный вклад сил тяжести).

3.2.2. Гипотеза сплошной среды.

Хотя жидкости - квантованы в масштабе длины межмолекулярных расстояний (порядка 0.3 nm для жидкостей и 3 nm для газов), они предполагаются непрерывными в большинстве случаев микрофлюидики. Гипотезы континуума (непрерывности, сплошной среды) предполагает, что макроскопические свойства флюида, состоящего из молекул, те же самые, как если бы флюид был совершенно непрерывен (структурно однороден). Физические характеристики: масса, импульс и энергия, связанные с объемом флюида, содержащего достаточно большое количество молекул, должны быть приняты как сумма соответствующих характеристик всех молекул.

Гипотеза континуума ведет к концепции жидких частиц. В отличие от идеальной точечной частицы в обычной механике, жидкая частица в флюидной механике имеет конечный размер. В атомном масштабе (используя современный СЗМ) мы столкнулись бы большими флуктуациями из-за молекулярной структуры флюидов, но при увеличение объема пробы, мы достигаем уровня, где возможно получение устойчивых измерений. Такой объем пробы должен содержать достаточно большое количество молекул, для получения достоверного воспроизводимого сигнала с маленькими статистическими колебаниями. Например, если определить требуемый объем как куб со стороной 10 нм, то такой объем содержит приблизительно 4x104 молекул и определяет уровень флуктуаций порядка 0.5%.

Важнейшим положением, нуждающимся в проверке, является допустимость анализа массопереноса вещества на основе модели сплошной среды, что позволяет использовать концентрационные зависимости вместо статистического анализа

25

А.А. Евстрапов. Курс лекций «Нанотехнологии в экологии и медицине»

ансамбля отдельных частиц. Положение о модели сплошной среды рассматривается как необходимое условие микрофлюидики.

Анализ применимости гипотезы проводится на основе сравнения длины свободного пробега частицы с характерным геометрическим размером d. Отношение этих длин – число Кнудсена: Kn = λ / d , где λ – длина свободного пробега в газе или жидкости. На основе оценок числа Кнудсена определяются два важных положения: а) при Kn менее 10-3 гипотеза сплошной среды обоснована, б) при Kn до 10-1 допустимо применение условия прилипания частиц к жестким стенкам канала. Сама формулировка последнего условия также может быть различна: как в форме U=0, так и в более сложной форме, связанной с касательными напряжениями. Расчет λ можно

осуществить как λ ≈ 3 V / Na , где V - молярный объем, Na – число Авогадро. При определенных геометрических аппроксимациях частиц вещества длина свободного

пробега может быть вычислена как λ ≈1/( 2πrs2 Na ), если использовать в качестве rs

радиус Стокса, как следствие сферической аппроксимации частицы. С другой стороны, для модели жесткоцепной молекулы rs следует заменить на характерный размер

частицы – радиус инерции Rg, вычисляемый как Rg = ni 6δl . Здесь δl – длина одного

фрагмента цепочки (звена), ni – число звеньев.

Разумеется, гипотеза сплошной среды неприемлема, когда рассматриваемая система приближается к молекулярному масштабу. Это случается в нанофлюидике, например, при жидком транспорте через nano-поры в мембранах клеток или в искусственно сделанных наноканалах.

3.2.3. Базовые теоретические положения

Теоретическую основу для реализации электрофореза и других сепарационных методов составляют: а) уравнение неразрывности с системой уравнений Навье-Стокса (для ввода вещества давлением), б) система уравнений Пуассона-Больцмана для электростатического потенциала и для скоростного профиля (для электрокинетического управления потоками), в) дополнительно к предыдущему, теория двойного электрического слоя, г) при наличии нескольких источников движения потока, например, давление и электрокинетика, соответствующие конвективные скорости складываются. Такая аддитивность следует из принципа суперпозиции только при условии линейности скоростей.

При управлении давлением распределения конвективной скорости в цилиндрическом микроканале и коаксиальном капилляре определяются геометрией

Здесь r — радиальная координата сечения микроканала (коаксиала), R — радиус канала, r1,2 — внутренний и внешний радиусы коаксиала, максимальная V* и средняя <V> скорости пропорциональны градиенту давления; вспомогательные параметры

Выражение для профиля конвективной скорости в плоской щели аналогично выражению для профиля скорости в круглом капилляре с учетом замены r и R на координату сечения y и полуширину щели h соответственно.

26

А.А. Евстрапов. Курс лекций «Нанотехнологии в экологии и медицине»

Формирование скоростного профиля происходит в соответствии с уравнениями Навье-Стокса и неразрывности: система уравнений Навье-Стокса для компонент

градиента и дифференциального оператора Лапласа соответственно. В прямоугольных декартовых координатах их явные выражения

В криволинейных координатах, в т.ч. цилиндрических и сферических их вид более сложен. Соответствующие выражения можно найти в любом учебном пособии по математической физике.

Чаще всего в прямолинейных каналах микрофлюидных систем конвективная скорость имеет только одну аксиальную составляющую. Систему Навье-Стокса

традиционно дополняет уравнение неразрывности (сплошности) ρ v = 0.

Для расчета массопереноса (профиль концентраций C=C(x,y,z,t)) и теплопереноса (профиль температур Т=Т(x,y,z,t)) используется аналогичные уравнения с заменой коэффициента динамической вязкости μ на коэффициент диффузии (D) или термодиффузии (χ). В правой части уравнений производится замена «вязкого» слагаемого μ v на диффузионное D C или термодиффузионное χ T

соответственно, и также могут быть дополнительные источниковые/стоковые слагаемые, связанные с выработкой или расходованием вещества или тепла. Заметим, что такой вид имеют уравнения при предположении о постоянстве коэффициентов динамической вязкости, диффузии и термодиффузии.

Рассмотрим уравнение Пуассона-Больцмана для распределения потенциала по сечению канала в случае симметричного электролита с двумя моновалентными ионами:

Здесь li — валентность i-го иона, е — заряд электрона (1.6.10-19 Кл), F — постоянная Фарадея (9.65.104 Кл/моль), с0 — молярная концентрация ионов компонент (моль/м3), Т

— температура (К), кb — постоянная Больцмана (1.38.10-23 Дж/К), φ — потенциал, z — нормированная пространственная координата сечения, sh — функция гиперболического синуса.

На границе раздела сред жидкость-твердое тело (поверхность канала) выделяют два пристеночных слоя: слой Штерна (Stern layer) и Гоуи-Чепмена (Gouy-Chapman layer), причем толщина второго связана с Дебаевской длиной электролита λD. В большинстве случаев допускается линеаризация уравнения Пуассона-Больцмана (т.к. при малости аргумента гиперболического синуса последний заменяется аргументом, т.е. sh(x)≈x) и использование т.н. приближения Дебая-Хаскела.

распределения потенциала в канале преобразуется к уравнению гармонических

колебаний. ΔΦ = 12 Φ.

λD

27

А.А. Евстрапов. Курс лекций «Нанотехнологии в экологии и медицине»

Б) Для линеаризации требуется выполнение β =( Fξ0 ) /( RT ) <1 и sh( βξ ) ≈ βξ .

(F и R обозначают, соответственно, постоянную Фарадея и универсальную газовую постоянную). Линеаризованное уравнение Пуассона-Больцмана, описывающее

Решением должна быть комбинация вещественных экспонент или гиперболических функций. Граничные условия: симметрии ddzξ z=0 = 0 (заметим, что по форме это

условие совпадает с условием непроницаемости) и электростатического баланса ξ z=1 =1, так как на стенке потенциал совпадает с дзета-потенциалом. Параметр λ есть

обратная величина от дебаевской длины.

Распределение относительной величины потенциала описывается выражением

ξ = ch( λz ) / ch( λ ).

Следствием линеаризации уравнения Пуассона-Больцмана для потенциала будет уравнение для скорости электроосмотического потока (скоростного профиля) в форме:

канала и прилипания к стенке канала (u=0). Здесь Е=U/L – напряженность электрического поля.

Качественные закономерности формирования профиля конвективной скорости: а) поскольку вторая производная (радиус кривизны) скоростного профиля пропорциональна потенциалу, неравномерность распределения потенциала приведет к усилению неравномерности скорости по сечению канала, б) аппроксимировав профиль

выражением umax (1− z m ), где m – показатель, характеризующий клиновидность

профиля, можно связать m c заданными условиями, а именно, дзета-потенциалом ξ0, шириной канала 2h, напряженностью электрического поля Е, концентрацией буфера С0,

вычислить Дебаевскую длину в метрах.

При типичной биохимической концентрации буфера (1-10) мМоль/л, эта величина составляет несколько нм. Характерной величиной дзета-потенциала является 10-50 мВ. Толщина двойного электрического слоя (EDL) составляет несколько λD. В ряде работ говорится о четырехкратной Дебаевской длине при λD=3 нм. Количественно эта толщина при традиционных условиях анализа оценивается около 10 нм, т.е. единицыдесятки нм по сравнению с микрометровыми размерами канала. Типичным для электрофореза на микрочипе и, тем более, для его макроаналогов (капиллярного

электрофореза), является отношение λD / gd ≤10−4 . Т.о. вклад двойного

электрического слоя в формирование профиля конвективной скорости достаточно мал, и практически для всего сечения конвективная скорость постоянна (т.н. клиновидная форма профиля). В степенной аппроксимации такому профилю будет соответствовать

28

А.А. Евстрапов. Курс лекций «Нанотехнологии в экологии и медицине»

большой показатель степени m и, как следствие, максимальная скорость u* будет практически совпадать со средним значением скорости.

Некоторые решения уравнения Пуассона-Больцмана в приближении ДебаяХаскелла приведены далее. Например, для скоростного профиля в круглом

функция Бесселя нулевого порядка первого рода. Качественно схожим, будет выражение для скорости электроосмотического потока в плоской и прямоугольной

щели: u( z ) =V * 1− ch(αz ) , где коэффициент пропорциональности α выражается

ch(α )

по-разному. Например, уравнение для скоростного профиля в плоской щели примет

скоростного профиля уже для прямоугольного сечения в вертикальном (вдоль оси z)

сечения. При всем отличии механизмов формирования скоростного профиля, его аппроксимации качественно одинаковы.

Распределение концентраций в микроканалах в общем случае может описываться уравнением Навье-Стокса при условии, что гипотеза сплошной среды применима.

В некоторых простых случаях возможно получение аналитических решений для профиля концентраций при упрощающем положении о том, что конвективная скорость имеет лишь одну составляющую. Обычно это характерно для прямолинейных каналов. Решение осуществляется известными методами разделения переменных (Фурье).

Во многих случаях существует более простой подход, позволяющий получать приближенные аналитические («оценочные») решения. В качестве примера рассмотрим конвективно-диффузионный массоперенос в прямолинейном микроканале прямоугольного сечения. Сечение интерпретируем как совокупность одинаковых плоских щелей, т.е. получим плоскую пространственно двумерную задачу.

Уравнение Навье-Стокса примет вид

Здесь C=C(x,y,t) распределение концентрации вещества, U(y) – профиль аксиальной составляющей конвективной скорости (других составляющих аксиальная скорость не имеет), x – аксиальная (маршевая) координата, вдоль которой осуществляется конвективное движение вещества, y – ортогональная координата сечения, D — коэффициент диффузии.

Приближенные аналитические решения при дополнительных упрощающих предположениях, можно получить на основе метода моментов. Предполагаем, что вещество не может перемещаться на бесконечно большие расстояния по аксиальной координате.

Введем моменты порядка n, определяемые как

29

А.А. Евстрапов. Курс лекций «Нанотехнологии в экологии и медицине»

Данная формула содержит граничные условия 2-го рода, являющиеся следствиями непроницаемости стенок для вещества и симметричности канала (плоской щели). Учитывается естественное условие недоступности вещества в форме

∂pC( ±∞,y,t ) = 0; p = 0,1,2,.... Последнее условие говорит о невозможности ухода

∂x p

анализируемого вещества на бесконечное (очень большое) расстояние от зоны анализа. Начальные условия связаны с характером заполнения канала пробой и с объемом пробы.

Подобный метод решения – метод моментов, оперирует уже не концентрациями вещества, а концентрационным пиком. Нетрудно убедиться, что по аналогии с теорией вероятностей, момент μ0 имеет смысл общего количества вещества, отношение CT=μ1/ μ0 определяет центр тяжести аналитического пика, его дисперсия определяется как

σ 2 = μ2 / μ0 −CT 2 .

Здесь D* = D / h2 ,u* = u / h; h – полуширина щели, D, u – коэффициент диффузии и максимальная конвективная скорость, z=y/h – относительная координата сечения, отсчитываемая от оси (z=0 на оси щели, z=1 на стенке). Предварительно получена степенная аппроксимация профиля конвективной скорости (т.е. найден параметр m).

Исходное предположение также включало следующее начальное условие: в начальный момент времени анализируемое вещество имеет вид компактной короткой «пробки» длины 2δ или нормированной длины 0=δ/h. Очевидно, что решения μn зависят не только от времени t, но и от координаты сечения z (т.е. концентрационные пики в разных сечениях сдвинуты относительно друг друга – имеют различные центры тяжести и дисперсии, т.е., ширину).

Получены формулы для усредненных по сечению микроканала координаты центра тяжести аналитического пика компоненты и дисперсии пика:

< CT >=u* B0t

Здесь Pe=u*/D*, Bj — коэффициенты разложения конвективного скоростного профиля (1-zm) в ряд Фурье по косинусам, т.к. профиль симметричен. Обозначив

можно показать, что для профилей с большей клиновидностью (большими m) суммы S1 и S2, входящие в выражение для дисперсии уменьшаются. Для m – целых на основе таблиц можно получить следующие численные оценки:

Таблица 3.2.1 30