9.4.Модулирующие системные функции и импульсные характеристики
Следующий шаг в рассмотренииLTVканалов – представление модулирующих системных функций в терминах полосы пропускания. Напомним, что для любого комплексного сигнала u(t) ограниченного полосой пропускания W/2, модулированного реальным сигналом x(t) вокруг несущей частоты:
x(t) = u(t) exp{2πifct} + u∗(t) exp{−2πifct}.
Предположим далее, что W/2<<fc
В
условиях преобразования,
. Положительно-частотная
часть x(T)
- это просто смещенная вверх по fc(T).
Для пониманиямодуляции
и демодуляции в простейшем виде,
рассмотрим полосы комплексного
синусоидального входа e2πift
при f ∈
[−W/2, W/2] как модулированные, передающие
по каналу и демодулированные. (см. рис
9,6).Поскольку
канал может быть предметом доплеровского
сдвига, восстановленная несущая, ˜ fc,
в приемнике может отличаться от
фактической fc
несущей.Таким
образом, как показано на рисунке,
положительно частотный канал на выходе
и демодулированный сигнал
Для
произвольной полосы ограниченного
входа,
положительно частотный выходной канал
определяется как суперпозиция
.
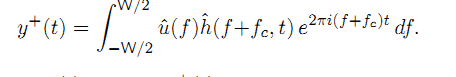Демодулированный сигнал, V (T) – это у + (T), смещенная вниз по восстановленной несущей ˜ fc, т.е.,
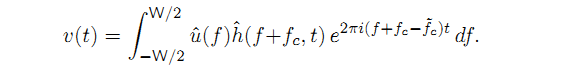
Пусть
Δ будет разницей между возвращенной и
переданной приемнику,
Тогда:
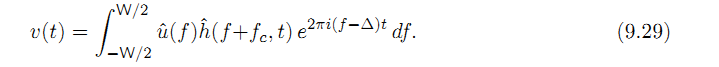
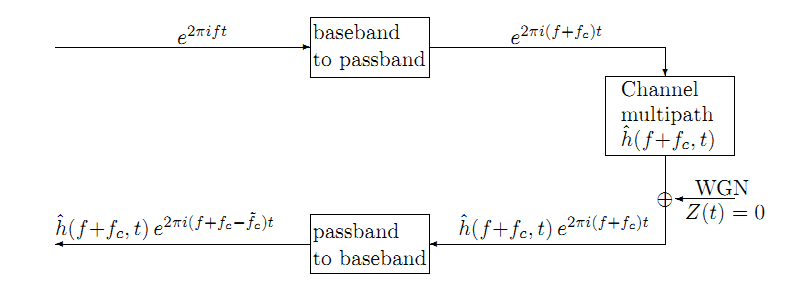
Рис. 9.6
Комплексные синусоидальные полосы,какмодулированные к полосе пропускания, проходят через многолучевой канал, и демодулируются без помех.
Модуляции образуется около несущей частоты FC и демодулируется на другой частоте ˜ fc.
Отношение
между входной u(t) и выходной v(t) в
полосе частот может быть выражено
непосредственно в терминах частотной
системной функции
,
определенной как
Тогда (9.29) становится
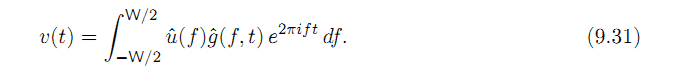
Позволяющий
быть импульсной LTV полосой, тот же аргумент, который использовался для получения уравнения свертывания полосы пропускания, приводит к
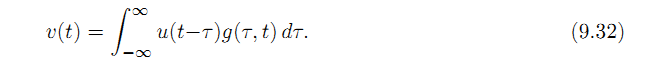
Интерпретация
этого уравнения свертывания полосы LTV
аналогично уравнению свертывания полосы
пропускания LTV (9,18). Для упрощенной
многолучевой модели,
и таким образом, системная функция полосы
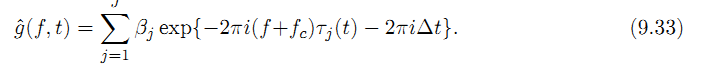
Мы можем разделить зависимость T от F, переписав это как
,
где
Взяв обратное преобразование Фурье для фиксированных t, импульс LTV полосы на выходе будет
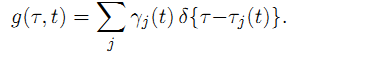
