9.3.Модель ввода/вывода беспроводных каналов связи

В этом разделе каналы связи, состоящие из произвольного набора электромагнитных путей J, рассматриваются как абстрактная модель ввода вывода. Например, при использовании отражающей поверхности существует прямой и отражённый путь, поэтому в данном примере J равен 2. В некоторых случаях может быть один прямой путь и несколько отражённых, исходящих от разных объектов. В других случаях прямой путь блокируется и существуют только косвенные.

Во многих ситуациях, складывающихся физически, основные пути сопровождаются побочными и ослабленными путями. Этом случае побочные пути исключены из модели и рассматривается только количество оставшихся основных путей.

Как и в других примерах предыдущего раздела, основной путь J имеет задержки и ослабления, происходящие из-за длины пути, характеристик антенн и отражателей. Например, в рисунке 9.5. сигналполучаемый на приёмной антенне, проделавший путь j и поданный на передающую антенну exp(2πift) вычисляется как:

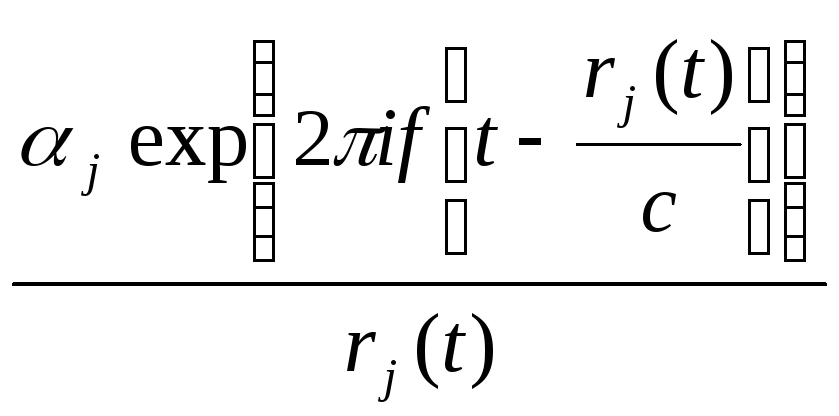
Тогда общий ответ на приёмную антенну при вводе exp(2πift):

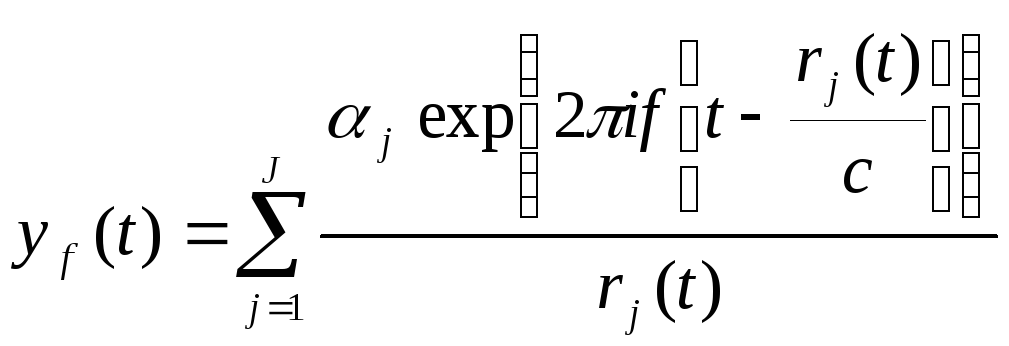
(9.11)

В примере с идеально отражающей поверхностью приёмная антенна, собирающая сигналы, получает по прямому пути α₁, которое обозначается как α в (9.9). Также приёмная антенна получает по отражённому пути α₂, которое обозначается как –α, потому что при отражении происходит смена фазы сигнала. Длина пути r₁(T) = r₀ – vtи r₂(T) = r₀ – vt делает (9.11) эквивалентно (9.9) в этом примере.

В общем случае основных путей J более удобно заменить (9.11) выражением с явным с явными ослаблениями β_j(t) и задержками τ_j(t)на каждом пути.

(9.12)

(9.13)

Уравнение (9.12) может быть также использовано для скоростей затухания, отличных от 1/r². Выражение (9.11) можно переписать также в виде:

где

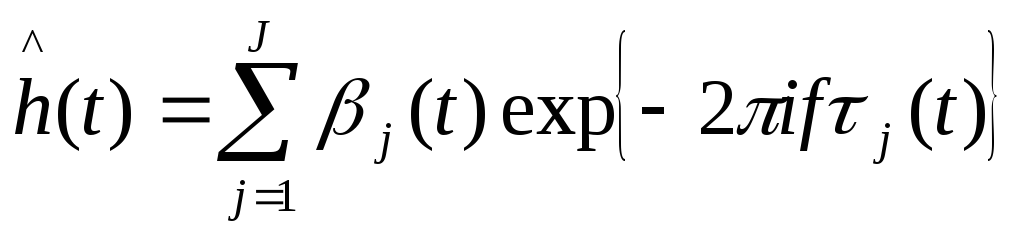
(9.14)

Функция h(f, t) аналогична функции h(t) линейной, не изменяющейся со временем системы (LTI), за исключением изменений в переменной t. h(f, t) называется функцией линейной, изменяющейся со временем системы (LTV).

Затухание β_j(t) медленно меняется со временем и частотой, но эти изменения пренебрежительно малы для данной модели. Упрощённая модель часто используется, когда затухание можно обозначить постоянной β_j._.Также в этой модели предполагается, что задержки в каждом пути меняются линейно τ_j(t) = τ_j⁰ + τ^’_jt. Функция h(f, t) в упрощённой модели может быть записана:

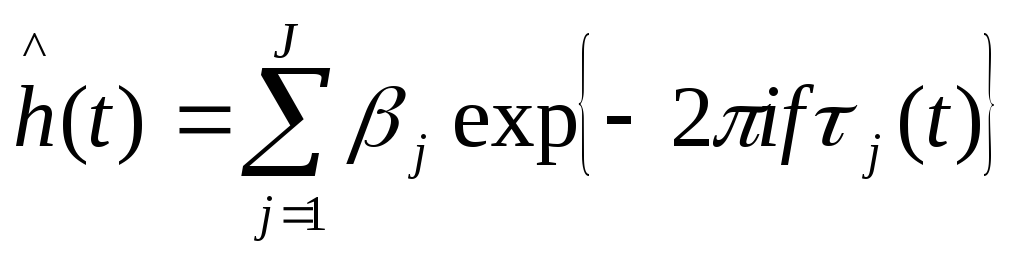где τ_j(t) = τ_j0 + τ^’_jt

(9.15)

Такая упрощённая модель может быть использована при анализе отражающей поверхности. β₁ = -β₂ = α/r₀, τ₁⁰= τ₂⁰ = r₀/cи τ^’₁ =-τ^’₂ = -v/c.

9.3.1. Системная функция и импульсный отклик в ltv системах

Системная функция LTVсистем h(f, t) в (9.14) была определена для каналов с несколькими путями и ограниченным числом путей. Упрощённая модель была определена в (9.15). Системная функция может быть также обобщена для непрерывного множества путей. В общем, если y_f(t) является результатом на ввод exp(2πift), тогда h(f, t) определяется как y_f(t)exp{-2πift}.

В этом пункте, h(f, t)exp(2πift) является результатом на ввод exp(2πift) на каждой частоте. Цель состоит в том, чтобы найти значение на ввод произвольного x(t). Для этой цели необходимо обобщить известные уравнения и перейти от случая LTI к LTV.

Ключевым предположением в этом обобщении служит линейность системы. Т.е. если y₁(t) и y₂(t) являются значениями на ввод x₁(t) и x₂(t) соответственно, то α₁y₁(t) + α₂y₂(t) является значением для α₁x₁(t) + α₂x₂(t), что следует из уравнений Максвелла.

Используя линейность, значением на наложение набора синусоид

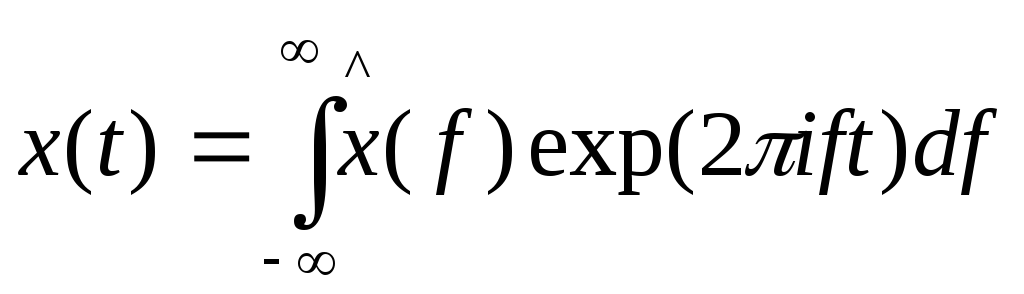служит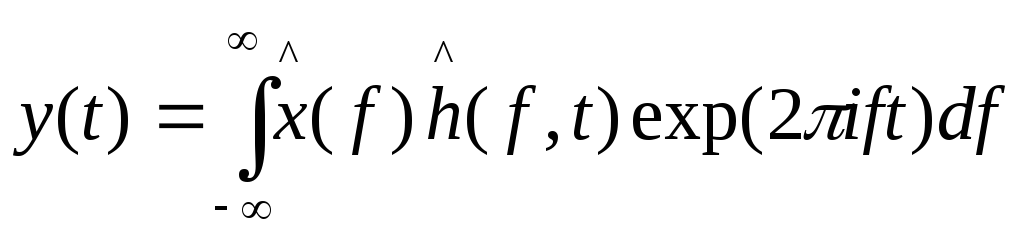

(9.16)

Здесь существует соблазн слепо подражать теории систем LTI и запутать преобразование Фурье для y(t), а именно y(f) с x(f)h(f, t). Это неверно логически и физически. Неправильно логически, потому что x(f)h(f, t) является функцией от t и f, а y(f) – только от f. Физически это неправильно, т.к. Доплеровские сдвиги приведут к значению от x(f)exp(2πift), содержащему несколько синусоид в f, а не одной синусоиды. С точки зрения получателя y(f) зависит от x(f) от f лежащего в определённом промежутке вокруг центрального значения f.

К счастью (9.16) может быть использовано для получения удовлетворительной формы импульсного отклика и уравнения характеристик импульса. Определить значение, изменяющегося во времени значение импульсаh(τ, t)поможет обратное преобразование Фурье функции h(f, t), где t рассматривается как параметр.

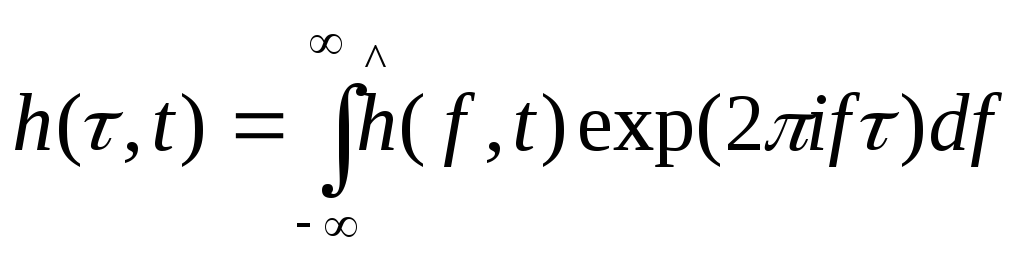
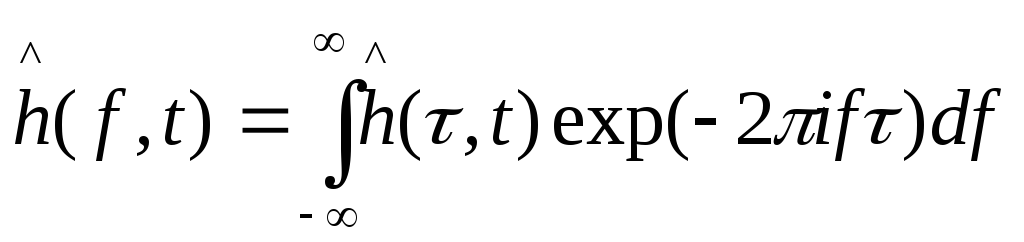
(9.17)

h(f, t) рассматривается как обычная системная функция LTIсистемы, которая постепенно изменяет своё значение от t и h(τ, t), и как значение импульса канала, изменяющегося от t. Подставляя вторую часть (9.17) в (9.16) получаем:

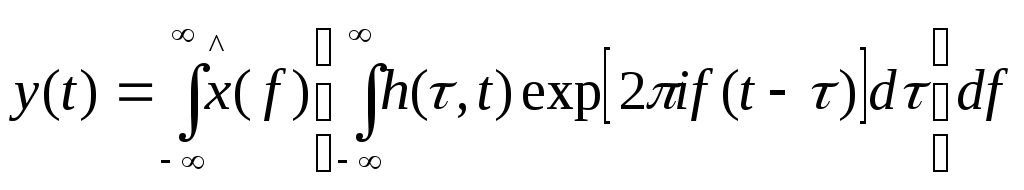
Поменяв порядок интегрирования:

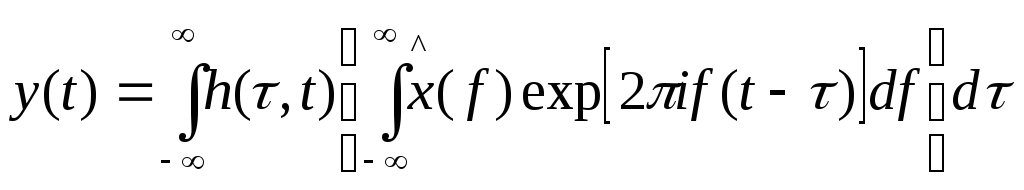
Обознача внутренний интеграл как x(t–τ), получим уравнение характеристики импульсов для LTV фильтров.

(9.18)

Это выражение говорит о том, что эффекты мобильных приёмников и передатчиков и произвольно движущихся отражателей и поглотителей имеют сложность уравнений Максвелла. И наконец можно свести ввод/вывод между передающей и принимающей антенной к уравнению характеристик импульса для LTV фильтров. Так h(τ, t) является значением импульса в момент t до импульса в момент t-τ. Если h(τ, t) не меняет значения от t, то как функция от τ, h(τ, t) является обычным значением импульса LTI.

Этот вывод относится к реальным и сложным системам. Фактические физические значения ввода x(t) должны быть реальными, как впрочем и физические значения вывода y(t). Отсюда и из (9.17) следует, что h(-f, t) = h*(f,t), которое определяет f>0;

Есть многосходств между результатами фильтров LTVи фильтров LTI. В обоих случаях выходной сигнал представляет собой изменение входного сигнала с импульсной характеристикой, в случае с LTI: y(t) = ∫ x(t − τ )h(τ )dτ, а в случае LTV y(t) = ∫ x(t − τ )h(τ, t)dτ. В обоих случаях системная функция является функцией характеристик импульса с проведённой над ней преобразованием Фурье. Для фильтров LTIh(τ) ↔ h(f), а для фильтров LTVh(τ, t) ↔ h(f, t). Т.е. для каждого tфункция h(f, t) является преобразованием Фурье функции h(τ, t) (по параметру t). Наиболее существенным отличием является то, что y(f) = h(f) x(f) в случае с LTI и обратным преобразованием Фурье h(f, t) x(f) для LTV.

Важно понимать, что сходство системной функции и функции характеристик импульса действительно для любой LTV системы и не зависит от упрощений модели с многими путями (9.15). Упрощённая модель ценна в понимании, как множество путей и изменяющееся со временем затухание влияет на передающийся сигнал.

Для упрощённой модели (9.15) h(τ, t) может быть легко выражены из h(f, t), как

↔

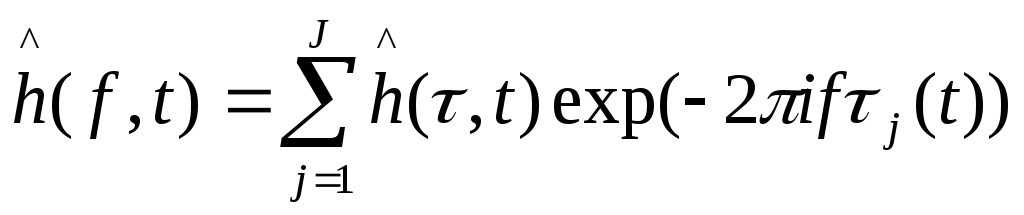_(9.19)

Где- дельта функция Дирака. Подставляя (9.19) в (9.18)

(9.20)

Данное выражение говорит о том, что вывод(отзыв) в момент tдо произвольного ввода является суммой ответов по всем путям. Вывод на путь J является тем же вводом, только с задержкой и ослаблением.Оба параметра измеряются во время замера.

Абстрактные, не физические импульсы в (9.19) возникают, потому что вводиться предположение об ослаблении и задержках, не зависящих от частоты. Как видно из (9.16) h(f, t) влияет на вывод, только в полосе частот, когда x(t) не равно нулю. Для других частот такого влияния нет. Разумное предположение для приложений работающих в узком диапазоне.

Ни общие результаты о системах LTV, ни результаты многолучевой модели (9.14) и (9.15) не дают непосредственного описания о затухании. Этот вопрос рассматривается в следующих разделах: сначала для синусоидального ввода, затем и для общего узкополосного.