19.Фракталы

Фрактальная графика основана на автоматической генерации изображений пу- тем математических расчетов. Создание фрактальных изображений основано не в рисовании, а в программировании. Фрактальная графика редко используется в печатных или электронных документах.

Фрактал— геометрическая фигура, обладающая свойством самоподобия, то есть составленная из нескольких частей, каждая из которых подобна всей фигуре целиком.

С точки зрения компьютерной графики, фрактальная геометрия незаменима при генерации облаков, гор, поверхности моря. Фактически найден способ легкого представления сложных неевклидовых объектов, образы которых весьма похожи на природные [10, 13]. Определение фрактала, данное Мандельбротом, звучит так: «Фракталом называется структура, состоящая из частей, которые в каком-то смысле подобны целому.»

Одним из основных свойств фракталов является самоподобие. В самом простом случае небольшая часть фрактала содержит информацию о всем фрактале. Фрактал можно определить, как объект довольно сложной формы, получающийся в результате выполнения простого итерационного цикла. Итерационность, рекурсивность обуславливают такие свойства фракталов, как самоподобие — отдельные части похожи по форме на весь фрактал в целом [13].

Мандельброт:zk+1 = z 2 k + z0, k = 0, 1, . . ., n

Цикл итераций для фрактала Мандельброта можно выполнять в диапазоне x = (от − 2.2 до 1), y = (от − 1.2 до 1.2). Для того чтобы получить изображение в растре, необходимо пересчитывать координаты этого диапазона в пиксельные.

Фрактал Джулия внешне совсем не похож на фрактал Мандельброта, однако он определяется итерационным циклом, почти полностью тождественным с циклом генерации Мандельброта. Формула итераций для фрактала Джулия такая:

Джулия:zk+1 = z 2 k + c,

где c — комплексная константа. Условием завершения итераций является ∣zk∣> 2 — так же, как для фрактала Мандельброта. На рис. 1.6 приведено два изображения фрактала Джулия для c = 0.36 + i⋅0.36, изображение построено в границах x∈[−1, 1], y∈[−1.2, 1.2].Нарис. 1.6,бпоказанувеличенный фрагмент фрактала. Как видим, фрактал самоподобный — при любом увеличении отдельные части напоминают формы целого.

Ньютон: zk+1 = 3z 4 k + 1 4z 3 k ,

где z — также комплексные числа, причем z0 = x + i ⋅yсоответствуеткоординатамточки изображения. Условием прекращения цикла итераций для фрактала Ньютон есть приближе- ние значений∣z 4 − 1∣кнулю.Например,изображениенарис. 1.7былополученодля∣z 4 − 1∣2 > 0.001, границы расчета x∈[−1, 1], y∈[−1, 1].

20.Фрактальное сжатие

Фракталы — удивительные математические объекты, подкупающие своей простотой и богатыми возможностями по построению объектов сложной природы при помощи всего лишь нескольких коэффициентов и простой итеративной схемы.

Именно эти возможности и позволяют использовать их для сжатия изображений, особенно для фотографий природы и прочих сложных самоподобных изображений.

Нам пригодятся следующие:

Метрика — функция, заданная на пространстве, возвращающая расстояние между двумя точками этого пространства. Например, привычная нам Эвклидова метрика. Если на пространстве задана метрика, оно называется метрическим. Метрика должна удовлетворять определенным условиям, но не будем углубляться.

Сжимающее отображение (преобразование)— функция на метрическом пространстве, равномерно уменьшающая расстояние между двумя точками пространства. Например, y=0.5x.

Сжимающие отображения обладают важным свойством. Если взять любую точку и начать итеративно применять к ней одно и то же сжимающее отображение: f(f(f...f(x))), то результатом будет всегда одна и та же точка. Чем больше раз применим, тем точнее найдем эту точку. Называется она неподвижной точкой и для каждого сжимающего отображения она существует, причем только одна.

Несколько аффинных сжимающих отображений образуют систему итерированных функций (СИФ). По сути, СИФ — это множительная машина. Она принимает исходное изображение, искажает его, перемещает, и так несколько раз.

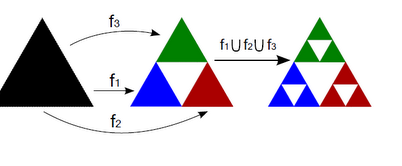
Например, вот так при помощи СИФ из трех функций строится треугольник Серпинского: