Теорема. Функция распределения случайной величины X, распределенной по равномерному закону, есть
|
0 |
|
, |
x a; |
|
x |
a |
|
|
|
|
|
||
F(x) |
|
|
, |
a x b; |
|
a |
|||
b |
|
|
||
|
1 |
|
, |
x b. |
Её математическое ожидание: |
M ( X ) a b |
||
|
|
||
и дисперсия |
|
2 |
|
|
|
||
D( X ) |
(b a)2 |
. |
|
12 |
|||
|
|
||
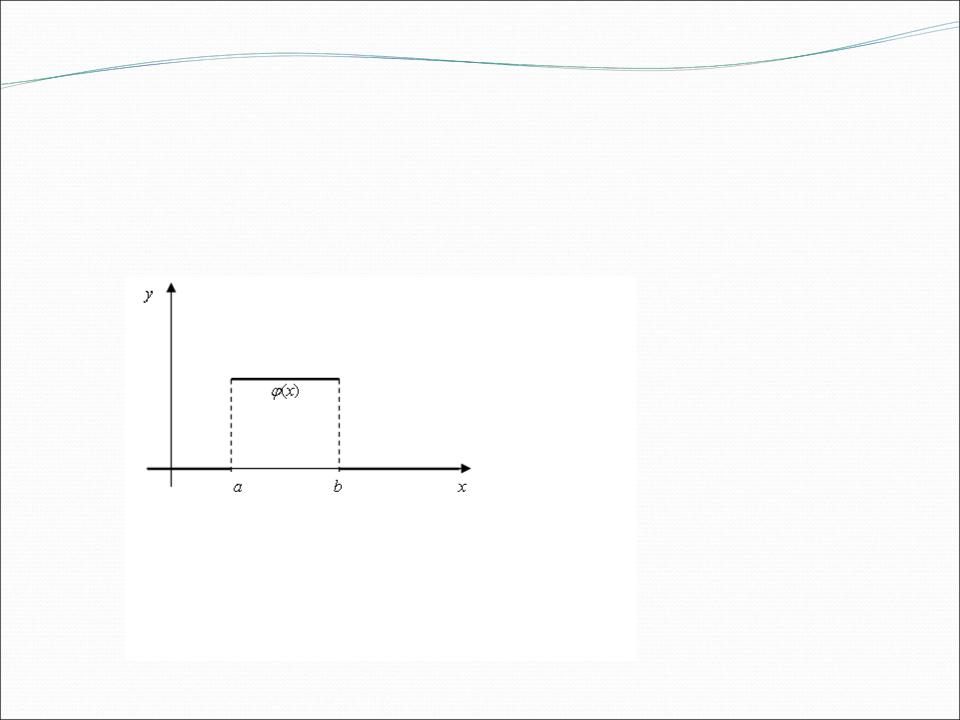
График плотности вероятности имеет вид:
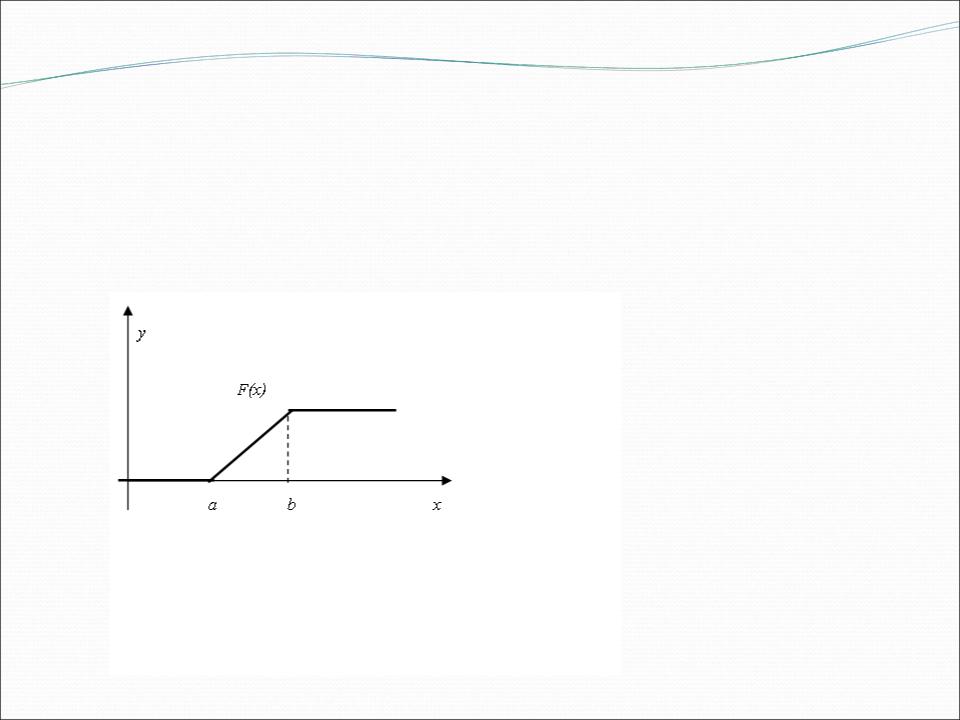
График функции распределения имеет вид:
Нормальный закон распределения
Непрерывная случайная величина X имеет нормальный закон распределения (закон Гаусса) с параметрами а и 2 , если её
плотность вероятности имеет вид:
|
|
|
|
|
|
(x a)2 |
|
1 |
|
|
2 2 |
|
|||
|
|
|
|
||||
(x) |
|
|
|
e |
|
|
, x |
2 |
|
|
|||||
Кривую нормального закона распределения, называют гауссовой кривой.
Теорема 1. Математическое ожидание случайной величины X, распределённой по нормальному закону, равно параметру а этого закона, а дисперсия параметру 2, т. е. М(Х) = a, D(X)= 2.
Функция распределении случайной величины X, распределённой по нормальному закону имеет вид:
|
|
1 |
|
x |
(t a)2 |
|
F(x) |
|
|
e |
2 2 dt. |
||
|
|
|
|
|||
|
|
|
||||
|
|
|
2 |
|
||
В частном случае, когда а=0, а 2=1 нормальное распределение называется
стандартным.
Теорема 2. Функция распределении случайной величины X, распределённой по стандартному нормальному закону, выражается через функцию Лапласа Ф0(х) по формуле
F(x) 1 |
Ф0 (x). |
|
|
|||||
|
2 |
|
|
|
|
|
|
|
где |
|
|
|
1 |
|
xe |
t2 |
|
Ф |
(x) |
|
|
2 dt. |
||||
|
|
|
||||||
|
||||||||
0 |
|
|
|
|
|
|
|
|
|
|
|
|
2 0 |
|
|
||
В общем случае |
F(x) |
1 |
Ф0 |
( |
x a |
). |
2 |
|
|||||
|
|
|
|
|
||
Свойства нормального распределения |
|
|
|
1. Вероятность попадания случайной величины X, распределённой по |
|||
нормальному закону, в интервал [х1, х2], равна |
|
||
P(x |
X x ) Ф0 (t2 ) Ф0 (t1 ) , где t1 x1 |
a , t2 |
x2 a . |
1 |
2 |
|
|
2. Вероятность того, что отклонение случайной величины X, распределенной по нормальному закону, от математического ожидания a не превысит величину > 0 , равно:
Р( Х а ) = 2Ф0 (t), t = .
По этой формуле можно рассчитать вероятности Р( Х а ), для различных значений :
= , Р( Х а ) = 2Ф(1)=0,6827;= 2 , Р( Х а ) = 2Ф(2)=0,9545;= 3 , Р( Х а ) = 2Ф(3)=0,9973.
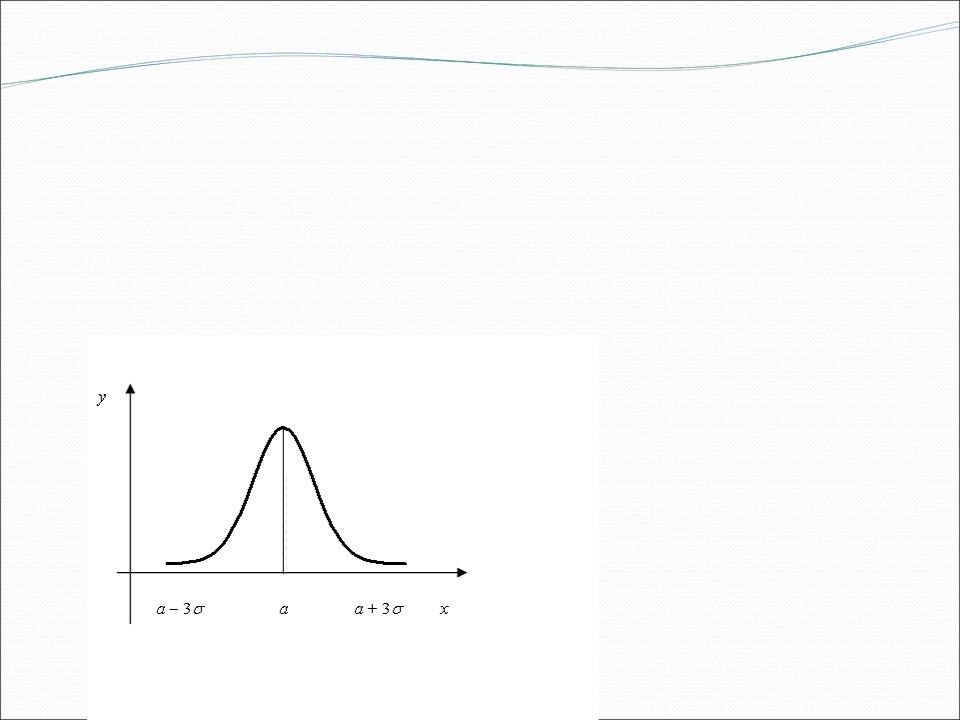
правило трех сигм
Если случайная величина распределена по нормальному закону с параметрами a и 2 , то практически достоверно, что её значения заключены в интервале от а 3 до a + 3 .