
Основы томографии
.pdf110
! $& $# $!$ $! /0 ")- ")" "& '+ -- 1&,1 !1 $, 2 $ $%$$ %" ) 1 !1 -$ ," # $) . $ , & $ 1 – -$ ," # $) . .
20 ")- ")" "& '+ -- " -,$! $! " " $,/3 !- $! " %,1 * , # $-"! "1 "! 7 "# & !", !&$ # "& ! ,/ $! " -$, 2","
--' 813 " 819 -$ , !!"(" *"" "– # [=65]: |
|
|
|
|
|
||||||||||
")- ")" "& 1 |
-- 8 13: |
|
|
|
|
|
|
|
|
|
|
|
|||
~ |
= a1x + b1, |
|
|
|
|
|
|
|
|
|
|
|
|
||
x |
|
|
|
|
|
|
|
|
|
|
(76) |
||||
~ |
|
|
|
|
2 |
|
|
3 |
|
n −2 |
|
|
, |
||
= a2 y + b2 + a3 x + a4 x |
+ a5 x |
+ + an x |
|
|
|||||||||||
y |
|
|
|
|
, |
|
|
||||||||
% n – 2"!,$ - ) $& --'; |
|
|
|
|
|
|
|
|
|
|
|
||||
")- ")" "& 1 |
-- 8 19: |
|
|
|
|
|
|
|
|
|
|
|
|||
|
~ |
= |
a2 x + b1 |
, |
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|||
|
1− a1x |
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
(77) |
||
|
|
|
a3 y + b2 + a4 x + a5 x2 + + an xn −3 |
|
|
|
|||||||||
|
~ |
= |
|
|
|
|
|||||||||
|
y |
|
|
|
|
|
|
|
. |
|
|
|
|||
|
|
(1− a1x) |
n−3 |
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||
$) $! $& '+ --, -,$! $! " )$ % #! &$& / --', !$- 1- 7 ' ! - 2"!, ')" [=65]. ,"* 6 !& % ' - ) ' .,"2 '+-- - $! ! & '+ - $ .$& "#.
6
) ! &
"% --' |
|
|
|
|
|
) |
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a1 |
|
|
a2 |
|
a3 |
|
|
|
a4 |
|
b1 |
|
b2 |
|||||
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
a |
|
b |
|
|
$"& 1 Gp |
|
det( Ap ) ≠ 0, Ap = |
1 |
|
2 |
1 |
|
|||||||||||
|
a3 |
a4 |
b2 |
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
a5 |
a6 |
1 |
|
|||
$ $,/ 1 - $"& 1 G |
|
|
|
|
|
A |
p |
AT |
|
= E |
|
|
|
|
|
|
||
op |
|
|
|
|
|
|
|
p |
|
|
|
|
|
|
|
|
|
|
((" 1 Ga |
|
|
|
|
a5 = 0 , |
a6 = 0 |
|
|
|
|
||||||||
$((" 1 G |
det(A |
|
) ≠ 0 , |
A |
|
= |
a |
a |
2 |
|
|
0 |
|
0 |
||||
|
|
|
1 |
|
|
|
|
|||||||||||
ca |
|
ca |
|
ca |
|
|
a3 |
a4 |
|
|
|
|
||||||
$ $,/ 1 ((" 1 Goa |
|
|
|
Aca AcaT |
= E |
|
|
|
|
|
|
|
0 |
|
0 |
|||
4 " Gu |
cosC |
|
|
sinC |
|
-sinC |
|
|
cosC |
|
0 |
|
0 |
|||||
")) "2$ $7 " Gs |
±1 |
|
|
0 |
|
|
0 |
|
|
|
±1 |
|
0 |
|
0 |
|||
!3 "$& " Gd |
k1 |
|
|
0 |
|
|
0 |
|
|
|
k2 |
|
0 |
|
0 |
|||
$%$" Gm |
k |
|
|
0 |
|
|
0 |
|
|
|
|
k |
|
|
0 |
|
0 |
|
$!$# !%&" -$ x Ghx |
1 |
|
|
k |
|
|
0 |
|
|
|
|
1 |
|
|
0 |
|
0 |
|
) 4 " Gc |
1 |
|
|
0 |
|
|
0 |
|
|
|
|
1 |
|
|
t1 |
|
t2 |
|
) 4 " ") !3 "$& " Gcd |
k1 |
|
|
0 |
|
|
0 |
|
|
|
k2 |
|
t1 |
|
t2 |
|||
) 4 " "-$%$" Gcm |
k |
|
|
0 |
|
|
0 |
|
|
|
|
k |
|
|
t1 |
|
t2 |
|
4 ""-$%$" Gum |
kcosC |
|
ksinC |
- ksinC |
|
|
kcosC |
|
0 |
|
0 |
|||||||
"2 ! 1Gcmu |
kcosC |
|
ksinC |
- ksinC |
|
|
kcosC |
|
t1 |
|
t2 |
|||||||

111
4.3.2. 0: 2 3 6 0 < 7
" $ ! $)$ ("2 ! ")" ".$ 7 "1)" $$ %" ' - '+$2 , - &",$, $- % ,10 !1 ! $3" $#, $ $ 1 - "&$%" $3"
- " $- % , "" - ) $& --$&$ $ - $ .$& "1 ", !, %! &" , $3" $ *"" $$ %" &! + $2 ".$ 7 "1. &"!")$! / $3" "$ *"" - $! ! & '+ "! 7 "# $2 ".$ 7 "1 (Dr) $ & ,"- 2" ' $3" " $- % , "1 $$ %" - $& (Dl) $!" - 1)$ - $-$ *"$-,/ '# + , - "2 ) $6(("*" - $-$ *"$ ,/ $! " . &"!" $ &"% --$&$ $ - $ .$& "1.
$ +$%")$ $ ) " /, 2 $ & !, 2 $%" $&$# & ,"2" ' Dr %,1 &! +- $& - " ((" $) - $ .$& "" &! $2 " ".$ 7 "1 ") 0 $%"-
$& 0 $3" $ *"" Dl, - " - $ "& $) – & ,"2" $3" " . &"- !" $ -$,$7 "1 $2 " -,$! $! ". - " Dr, - &",$, $ ,"- 2 0 !1 %,1 7%$ $ - , $ + - 1)$ - $-$ *"$ ,/ $# . &"!"- )$! " ) 7% Dr " Dl %,1 $2 -,$! $! " !$+ 1 !1.
$%' $ *"" - $! ! & '+ "! 7 "# ".$ 7 "#, $! $-
& ' &'2"!, "" - ) $& $ $ $ - $ .$& "1 -$ $$ %" )- '+ $2 , -$.&$,10 ! $)- !" $& / "! 7 "1, $-"!'& )' -$, $#((" $# " - $ "& $# -- )". . ' $2 $! / - '+ $2 -$.&$,1
. 2" ,/ $ -$&'!" / $2 $! / &'2"!, "1 - ) $& - $ .$& "1.
,1 $-"! "1 ) $%" " $ *"" - $! ! & '+ "! 7 "# &$!- -$,/. )!1 -".$ 7 "1)" ( $) , - %! &,104 $ !$ $# 3 ! / 7 ! $! -, '+ 3- "* &, . -$, '+ &$%$# [=59].
' ) ".$ 7 "1+ - ' $2 " (* ' 6, ) $& ( $) )
" $ $!" ,/ $ "+ #% ) - ) ' --$&$ $ - $ .$& "1 ( "!. 67).
'2"!, ' - ) ' - ") ") * ,/ ') $2 ) 6, ) $& ( -$) " - $& "), !$$ & ! & ," - $ .$& $ ".$ 7 " 6 ,$ -
$) ! ") . $ 3 $! / $- % , "1 $$ %" $2 D = ±0,6 )).
) )
. 67. 1 ( ) ( )
" &'2"!, "" - ) $& ((" $ $ - $ .$& "1 & 2 ! & - -'+ '," &' ' $2 " T, U, V 6 ,$ $ $ ".$ 7 "1 " !$$ & ! & 04" ") $2 " T', U', V' "! 7 $ $ ".$ 7 "1 ( "!. 68). 6 $) !, 2 !!2"-
' - ) ' ((" $ $ - $ .$& "1 % !, % 04")": a1 = 1.035,
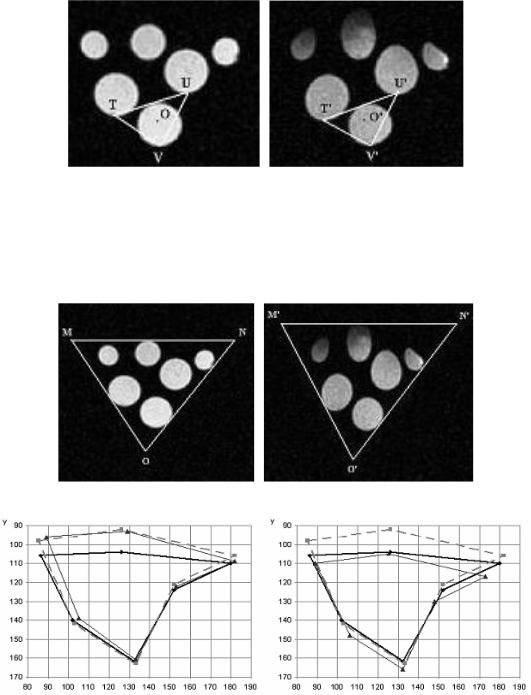
112
a2 = 0.045 , a3 = −0.065, a4 = 1.045 , b1 = −11.596 , b2 = 3.604 ( "!. 70, ).
. 68. % #
!," & 2 ! & - '+ &' / $2 " M, N, O %,1 6 ,$ $ $ ".$-
7 "1 " $2 " M', N', O' – %,1 "! 7 $ $ ( "!. 69), $ - ) ' (-
(" $# --' % % ")": a1 = 1.157 , a2 = −0.025, a3 = 0 , a4 = 1.179 , b1 = −15.46, b2 = −32.071 ( "!. 70, ).
. 69. 1
) |
) |
. 70. -
(–– –– , – – – –
, ––2–– )
,$ "2 ' &'2"!, "1 '," - $& % ' %,1 - $ "& $ $ - $ .$- & "1. ' $ 2 ' + - '+ $2 & !$$ & ! &"" ! "!. 68 -$.&$,",
$- % ," / |
!, % 04" |
- ) ' |
- $ "& $# |
--': a1 = 1.68, |
a2 = 0.463 , |
a3 = 0.04 , a4 |
= 2.118, a5 |
= 0.0008 , a6 |
= 0.003 , b1 = −88.947 , |
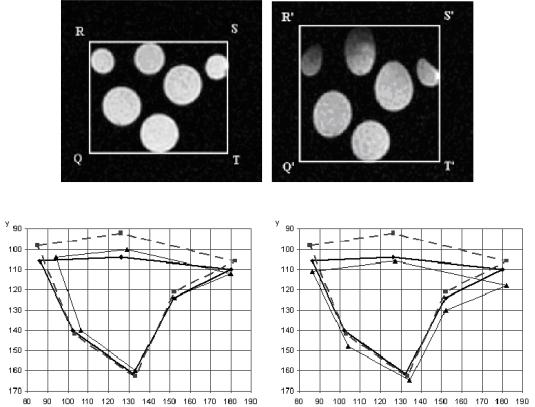
113
b2 |
= −89.384 ( "!. 72, ). " &' $ & 2 ! & - '+ $2 Q, R, S, T |
|||||||||||||
%,1 6 ,$ $ $ ".$ 7 "1 " $2 Q', R', S', T' – %,1 "! 7 $ $ ( "!. 71), |
||||||||||||||
- ) ' - $ "& $ $ - $ .$& "1 |
'," !, % 04")": a1 = 0.481, |
|||||||||||||
a |
2 |
= 2.484 ×10 |
−7 , a |
3 |
= −0.142 , |
a |
4 |
= 0.76 , |
a |
5 |
= −0.002 , |
a |
6 |
= 1.188 ×10−9 , |
|
|
|
|
|
|
|
|
|
|
|||||
b1 = 27.433 , b2 |
= 3.582 ( "!. 72, ). |
|
|
|
|
|
|
|
|
|
||||
. 71. % #
) |
) |
. 72. -
(–– –– , – – –
– , ––2–– )
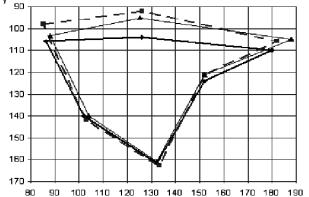
$ .$& " -,$! $! " ")- ")" "& $# --$# 819 . % !1 !"!-)$# & "# (77). %-$,$7"), 2 $ $2 " T, U, V 6 ,$ $ $ ".$ - 7 "1 !$$ & ! & 0 $2 ) T', U', V' "! 7 $ $ ".$ 7 "1 ( "!. 68).
' ) 6 " $2 " & 2 ! & - '+ " $ $!" ,/ $ "+ #% ) - -
) ' --$&$ $ ")- ")" "& $ $ - $ .$& "1 819: a1 = −3.278 ×10−3 , a2 = 1.859 , a3 = 1.523, a4 = 0.413 , b1 = −54.871, b2 = −66.298 . "!. 73 ",,0-
! " -$,$7 " * $& 6, ) $& ( $) -,$! $! " %,1 6 ,$ -$ $, "! 7 $ $ " - $ .$& $ $ ".$ 7 "#.
.,"2" - $ .$& $ $ " 6 ,$ $ $ ".$ 7 "# $ !,$&, $, &$- - &'+, ), 2 $ $$ %" ' - '+ $2 #% ' ! $3" $# ".-. - &$.)$7 $! " "+ $% $. 2 $ $ $- % , "1 - $".&$,/ $) ".$ 7 ""; &$-& $ '+, . ,/ ' $ .'& &,"1 " $3" .)'& "1 "! 7 -$ $ ".$ 7 "1.
114
. 73. -
319 (–– –– , – – – – -
, ––2–– )
", 23" . ,/ ' '," -$, 2 ' -$!, - $ .$& "1 ".$ 7 -"1 ")- ")" "& $# --$# 819, !$$ & ! & 04" 2 ' $2 " (A, D, E, F) %& + ".$ 7 "1+ !$&) ! ","!/. !$&- % " %& + $2 (B, C) $ !,$&, $ !",/ ') .)'& " ) "! 7 $ $ ".$ 7 "1. $- 6 $) " $, %$! $& ' % ' )$ ' / -$, 2 ' - " $) " *"".,"2 '+ --$&'+ - $ .$& "# %,1 . '+ 6, ) $& ".$ 7 "1.
4.4. 1 1 0 1 < 7 3 >5; 7 4-0: 7
$&' 6(( "& ' !-$!$ ' $ $ " ".$ 7 "# ! ," &$.)$7 ' !.&" " ) $ "" & #&, $&, $ $ ' -$ ! & "0 ! - $ .$& " ) -/ -$.&$,10 ! $ .%$ $,/3 # $2 $! /0 - %! &,1 / ) ,/2 #3" $!$-
$! " ( *"#, ".$ 7 "# " !" ,$&, &-,$ / %$ . '&$& - &$ $$% (! 2 $&), ! - "&1. $# "+ $ & ) " "," $$ %" ) - $! ! & .
)" «& #&, » && ," Alex Grossman " Jean Morlet & ! %" 1980-+ .
- ") " ,/ $ ,". ! #!)"2 ! "+ " ! "2 ! "+ !" ,$&. - ! $14 & )1 & #&, ' - ") 10 !1 & . % 2 + !-$. & "1 $ .$&, - " $ $ " !" . .,"2 '+ !" ,$&, - " ,". ".$ 7 "# .,"2-$# - " $%', %,1 !7 "1 $,/3"+ $ : )$& " ($ ) *"".
#&, -- $ .$& " !" , !$! $" & $ .,$7 "" -$ ."! , ! $ ! " $& $) ". $ , % 04 # $- % , ')" !&$#! & )" ( *"" (& #&, ), -$! %! &$) ) !3 '+ ".) "# " - $!$& [=38]. 7% 1 ". ( *"# 6 $ $ ."! + ". $- % , 0 - $! ! & 0
(& ) 0) 2 ! $ , " ,$ ,". *"0 & ("."2 ! $) - $! ! & (& - ) "). . ,/ -$1&,1 !1 &$.)$7 $! / ,"." $& / !&$#! & !" , $% $& ) $ & ("."2 ! $) (& )1, $$ %" ) " 2 ! $ $) - $! ! & +.
$ "" & #&, $& !" , s(t) - %! &,10 & &"% &.& 3 $# ! ))'
- $! '+ !$! &,104"+ – ."! '+ ( *"# ψ k (t) , ) $7 '+ $6(- ("*" ' Ck :
s(t) = Ckψ k (t) . |
(78) |
k |
|

115
."! ' ( *"" ψ k (t) - %-$, 0 !1 . % ')" & $- % , -
$) &"% , $ $,/ $ $6(("*" ' Ck !$% 7 " ($ ) *"0 $ $ $) !" , . ") $ .$), )$7 $ $&$ " / $ &$.)$7 $! " - %! &, "1 !" - ,$& $! $& 1%$& ! .,"2 ')" ."! ')" ( *"1)". - ") , 1% -/ "!-$,/. & 2 ! & ."! '+ ( *"# !" !$"%' " $!" !$"%'.
#&, ' + ". 0 !1 !&$")" & ) ') " 2 ! $ ') $ . )".
) $# $ . . % !1 $ $ $# ( *" # & ) " ψ (t) . 2 ! $ '#
$ . $- % ,1 !1 ( / -$ .$) ψˆ (ω) = F (ω) , $ $ '# . % |
$ "- |
04 0 !- & #&, . / -$ . $-"!'& !1 &' 7 " ) |
|
+∞ |
|
F (ω) = ψˆ (t)e−iωt dt . |
(79) |
−∞
% ". $! $&$-$, 04"+ "% # & #&, -- %! &, "1 !" ,$& . -,02 !1 & . "& !" , %& !$! &,104" – 0 ( -- $ !")"-04 0) " % ,"." 04 0 – ! -$!, % 04") "+ $2 " ) " *"$ -') ) $%$). 7%'# 3 $ $ $2 "1 !$$ & ! & $- % , $)$& 0 % $)-$."*"" " ! & *"" !" , .
$! $& - '& $ $ & #&, -- $ .$& "1 , 7" "!-$,/.$& " %& + - '& '+ " " " )'+ -$ &! # $!" t ("," ) ( *"#:
+∞
– & #&, -( *"" ψ (t) ! , &') . 2 " ) " , ( ψ (t)dt = 0 ),
−∞
$- % ,104 # % ," !" , " -$ $7% 04 # % ,"." 04" $6(("*"-
';
– ) !3 " 04 # ( *"" ϕ(t) ! %" "2 ') . 2 " ) " ,
+∞
( ϕ(t)dt = 1), $- % ,104 # $ - " ,"7 " !" , " -$ $7% 04 #
−∞
$6(("*" ' -- $ !") *"".
-- $ !")" 04" ( *"" ϕ(t) - "! 4" &! ) & #&, ), $,/ $
), $ $ ' $ $!1 !1 $ $ $ ,/ ').
,"." 04 1 ( *"1 ψ (t) !$.% !1 $! $& $# "," " $# ."!-
$# ( *"" ψ 0 (t) , $ $ 1, " ψ (t) , $- % ,1 "- & #&, . ."! 1 ( *"1 %$,7 %$&, &$ 1 / ) 7 $& "1), 2 $ " ( *"1 ψ (t) , "
$ !- 2"& / &'-$, " %& + $! $& '+ $- *"#:
–!) 4 " -$ $!" & ) " t −ψ 0 (t − b) - " b ;
–) !3 " $& " − a−1/ 2ψ 0 (at ) - " a > 0 " a + − {0}.
% a – - ) , $- % ,104"# 3" " 6 $ $ - ; b – $ -$,$7 " ., % 04 &' 7 " . % ! . %& 6 "+ !&$#! & ( *"" ψ (t) :
ψ (t) ≡ψ (a,b,t) = a −1/ 2ψ 0 (t −a b ).
116
") $ .$), %,1 . % '+ a " b ( *"1 ψ (t) " ! / & #&, . #&- , ', $ $. 2 )' ψ (t) , " $ % .'& 0 «) " ! ")" & #&, )"»,
-$! $,/ $ " -$ $7% 0 * ,'# 1% & #&, $& $- % , $ $ "- . "!-
$ & #&, -- $ .$& " ( ) !" , $- % ,1 !1 !$$ $3 " )
+∞ |
(80) |
(WΨ f )(k 2−s ,2−s ) = 2s / 2 f (t)ψ (2s t + k )dt . |
−∞
' 7 " (80) 1&,1 !1 $! $&$# %,1 & #&, - ,". !" ,$&. )." 0 !1 ) $%' (",/ *"" !" ,$&, $%" $& "1 !" ,$&, $-
) !3 $ $ ,". .
% 0 $-) !3 $ $ ,". . $ , John Mayer. - $* !!$ - $& % "1 "!!, % ) 1 ( *"1 -$%& !1 .,$7 "0 !$! &,104" ! .,"2 ') . 3 " ).
! / ( *"1 !$! $" ". ) %, $- " '! $) 104"+!1 ! ) $&.!," $ +$%")$ - %! &" / 6 ( *"0 $)- $ $% $) $& -- - $ !") *"", $ !, % "!-$,/.$& / 3 %"! ". *"" h , $- % ,1 )'# ". '! $) 104 $!1 ! ) ( *"". 9 $ - "& % $,/3 ) $,"- 2 ! & ,"3 # " ($ ) *"", $ $ 0 - "% !1 + " / " $ '& /.
%! &"& ( *"0 ! "!-$,/.$& " ) ! $,/ "+ . '+ 3 $& %"! "-
. *"", )' )$7 $ . 2" ,/ $ ) /3" / $,"2 ! &$ " ($ ) *"", $ +$- %")$ %,1 $2 $ $ &$!! $&, "1 ( *"".
! $& ')" $ , ! 1)" - ") "1 & #&, - ,". & $ $ ".$-
7 "# 1&,10 !1 (",/ *"1 " !7 " . 9 $ ) $% -$.&$,1 % ,1 / 3 ), . "& 1 . 2" ,/ $ "*' " $,/3" ! &$ ) , "+ % , #, 2 $ %,1 ) %"*" ! "+ ".$ 7 "# 1&,1 !1 & !/) & 7 ') [=25, =27]. % 1 & #&, -(",/ *"" . ,02 !1 & $), 2 $ ', - $& %1 $-) !3 $.,$7 " " -$, 2"& -- $ !") *"0 !" , " $ % ,". *"0, $ $-') $ .$) &$.% #! &$& / $6(("*" ' &'!$ $2 ! $ $# !$! &- ,104 # ( - ") , $ ," / $6(("*" ', . 2 "1 $ $ '+ "7 $ $ $- $ -$ $ ). ) - ) $ $ $ & #&, -- $ .$& "1 - $&$%1 &$!! -$&, " "!+$% $ $ !" , " -$, 2 0 $ (",/ $& $ ".$ 7 " . $% -$.&$,1 6(( "& $ -$% &,1 / 3 )' !$ !- )", $ ,"2 ')" $ ,$ $.
,1 - $& % "1 & #&, - $ *"" $ +$%")$ $- % ," / %& +) ' ) !3 ' ( *"" " %& +) ' & #&, '. ,1 ,0 $# ) !3 " 0- 4 # ( *"" ϕ " !$$ & ! & 04 $ # & #&, ψ -$! $") %& +) 0-- $ !")" 04 0 ( *"0 " " %& +) '+ & #&, , "!-$,/. 1 -
.$ $ - $".& % " :
ϕ(x, y) = ϕ(x)ϕ( y) ,
ψ H (x, y) =ψ (x)ϕ( y),
(81)
ψV (x, y) = ϕ(x)ψ ( y),
ψD (x, y) =ψ (x)ψ ( y).
117
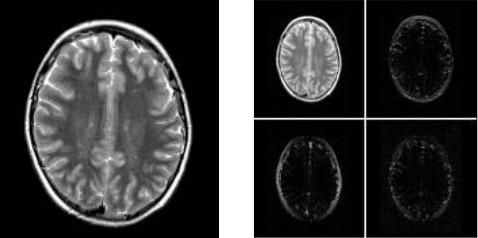
9 " & #&, ' ".) 10 & " *"" . 2 "# ( *"" – ".) "1 1 $- ! " ".$ 7 "# – -$ . ') - &, "1): ψ H ".) 1 & " *"" &%$,/ ! $, *$& (!&1. ' , - ") , ! $ ".$ ,/ ')" 1)" $ : $&), ψ V – &%$,/ ! $ (& " ,/ ' 1) " ψ D – &%$,/ %" $ , #.
$ 4 ) !, 2 & #&, - $ *"1 !$! $" ". !, % 04"+ 3 $&:
1) &' $ &'!$ $ $ $& 1 -- $ !") *"" j , $# 2 $ -- $ !") *"1 Pj (x) %$! $2 $ $2 $ $ 7 ( *"0;
2)&' $ , " ' .,$7 "1 N " +$7% " $6(("*" $& .,$- 7 "1 {cAN , cDN , cDN −1 ,..., cD1}, $- % ,104"+ - " ,"7 " ( *"" f (x) &
. % $) ) !3 ;
3)&$!! $&, " "!+$% $# ( *"" f (x) - " -$)$4" $ $ $ %"!-
$ $ & #&, -- $ .$& "1, ! "!-$,/.$& " ) -$, 2 '+ $6(("- *" $& .,$7 "1:
f (x) ≈ a j − N ,kϕ j − N ,k (x) + d j − N ,k Ψj − N ,k (x) +... + d j −1,k Ψj −1,k (x) . |
(81) |
||
k Z |
k Z |
k Z |
|
& +) $ )$7 ' / ,".$& $ ! -$)$4/0 $- *"# (",/ -*"" " - $ 7"& 04 # &' $ ". $! $,/ "!-$,/. )' ) !3 "-04 1 ( *"1 " & #&, -( *"" 1&,10 !1 .% ,")')", $ ! 2 , &'2"!,1 !1 $% $) $ '! $ & #&, -- $ .$& " ( ) -$ ! $-) $ ( *"" f(x,y), . ) &'2"!,1 !1 $% $) $ -$ ! $, * ) $ -$, 2 $ $ . ,/ .
) |
) |
. 74. 4 - : # ( ); -
' # ( )
'!$ $2 ! $ 1, "," % ,/ 1, 2 ! / + ". &'!$ $2 ! $ 0 & & " ,/ $) - &, "" !$! &,104 0 ".$ 7 "1. ". $2 ! $ 1 2 ! /, "," - " ,"7 " , !$% 7" " ($ ) *"0 $ ". "+ & & " ,/ $)- &, "" 2 ! $ +. $ ") 2 ! 1) ".$ 7 "1 . ) - ") 1 !1 - $* % (",/ *"" -$ ! $, * ) " - $ 7"& " . 9 $ % &'+$% 2 ' ".$ 7 "1 (2 ' 2 ! " "!+$% $ $ ".$ 7 "1).

118
,$ (",/ $& !" . !, 7" %,1 $ 4 "1 !!)$ $# &'3 - $* % '. $!! $&, " . ,02 !1 & $- *"" ! 4 04 # &' $ " " !& " ! %& )1 $% $) ')" (",/ )", $%" ". $ $ '+ % #! &
! $, *', % $# – ! $ ". ,$7 " -$, 2 '+ ") $ .$) -
. ,/ $& % - " ,"7 " j+1 ) !3 , -$!, 2 $ - $* % -$& $ 1-!1 %$ + -$ , -$ "!+$% $ ".$ 7 " % &$!! $&, $.
7%') & #&, $) )$7 $ !&1. / ! $,/ $ (",/ $&. " .,$7 -"" !" , ". $2 ! $ 0 " &'!$ $2 ! $ 0 !$! &,104" "!-$,/-
. 0 !1 %& (",/ .,$7 "1, $ $ ' $- % , ') $ .$) !&1. ' ! ) !3 " 04") (",/ $) W . $ ! *"" !" , 2 ! & 0 4 %& (",/ , $ $ ' 7 &'2"!,10 !1 -$ ) !3 " 04 ) (",/
W . ) !3 " 04") (",/ ) $ $!1 !1 & #&, -(",/ ' $ 3", !"), ', $#(, ', "$ $ $ ,/ ' " $ ' "$ $ $ ,/ ' !-, #-$&' (",/ ' [=42, =66]. ' $ $ $ $ & #&, &$ ) $ $) $- % ,1-!1 "!!, % )') !" ,$) " . % 2 )" ,". . 2" '& 1 + ' $!$ $! " .,"2 '+ & #&, $& &$ & ) $) " & 2 ! $ $) - $! ! - & , )$7 $ &'1&,1 / & ,"." )'+ !" , + "," " ' !&$#! & , $ $-' . ) ' "+ (" +, $!$ $ & - "! ! &"" !",/ '+ 3 )$&.!!)$ ") $!$ $! " $ $ '+ & #&, $&.
#&, > – - $! #3"# $ $ $ ,/ '# %"! '# & #&, , -$-$7% 04"# $ $ $ )" $& '# ."!. ,1 % $)-$."*"" !" , "!-$,/-
. 0 !1 %& ( *"": -- $ !")" 04 1 ( *"1, $ $ 1 & #&, > -
& 1 &! ) $)- $) $!" , , " % ,"." 04 1 ( *"1, $- -
% ,1 ) 1 !$$ $3 " )
1, |
x [0, 1 |
), |
|
|
ψ (x) = −1, |
|
2 |
|
(82) |
x [ 1 |
2 , 1), |
|||
0, |
x [0, 1). |
|
||
-- $ !")" 04 1 ( *"1 & % $) !, 2 .'& ! % "
. 2 "# !" , , % ,"." 04 1 . % -$ 1%$ - ") "1 - " 4 -
"# !" , , - "2 ) . 2 " +1 $. 2 !,$7 " , -1 – &'2" " .%$! )" & #&, > 1&,10 !1 , % $! /, . . . " "*'
& - $! ! & & ) ", &!, %! &" 2 $ &$. " 0 ! $ 2 ' '& 0- 4" «+&$! '», 7 $ ! ! &" !")) "" ($ ). !)$ 1 6 $, $ ") $)- '# $!" ,/ " $ !- 2"& &$.)$7 $! / $2 $# % $)-$-
."*"" " !" . ,0 $ $ !" , .
" ,". & #&, > )$7 -$ . /!1, 2 $ $6(("*" ' (",/ $& & #&, $& !!2" '& 0 !1 - $".&$,/ $. % $ 6 $ . 1987 . Ingrid Daubechies - %,$7", $ $ $ )" $& '# ."! & #&, $&,$ $ '# $! !1 ,02 &') " ! $% 1 %,1 ) $ "+ & #&, -- ",$7 "#.
$ ! " $& " & #&, $& $ 3" - $&$%" !1 $! $& ( *"#

119
ϕ(x) = |
2 |
hkϕ(2x − k ), |
ψ (x) = |
2 |
gkϕ(2x − k ) . |
(83) |
|
|
k |
|
|
k |
|
. $ $ $ ,/ $! " -- $ !")" 04 # " % ,"." 04 # ( *"# )$7 $ # ", 2 $ $6(("*" ' gk %,1 & #&, $& $ 3" $% $. 2 $ $--% ,10 !1 $6(("*" )" hk -- $ !")" 04 # ( *"". ,1 %$! -
$2 $ , % "+ ( *"# & #&, - $6(("*" ' $ 3" ) $ $ ) /3 & #&, - $6(("*" $& > , . . !" , )$7 $ !7 / ) $ $ !",/
- " -$)$4" & #&, $& $ 3". $! $,/ 6 " & #&, ' . ) $ $, , % " , $ $ - $ .$& " (!" .) 7 - $"!+$%" 6(( "& .
,1 - "2 ! "+ * , # ( - ") , & $ $ ".$ 7 "#) +$ ,$!/' ") / (",/ ! $ $ ')" !&$#! & )" !")) "". ".& ! $, $) !"! )' > , " 1 !"! ) ( *"# ψ ( ) " ϕ( ) )$7 $% $& -
) $ ") / $)- '# $!" ,/ " ' / !")) "2 $#. % $ )$7 $ -$- $ $& / - " ,"." /!1 !")) "". ,$ " ($ )' & #&, $ !")) "2 $# - $& 1 !1 ), ! $,/ $ !",/ $ $ ,$ 1 !1 $ ," # $#
. &"!")$! " ( . &' 7 "1 m0 (ω) = k hk exp(−ikω) . ") !")) -"2 ' & #&, ' -$, 2 0 - " )" ")". *"" 6 $# ( .'. #&, ', $ , - % 04" $ $ ')" !&$#! & )" !")) "" " -$, 2 ' ". & #&, $&$ 3", .'& 0 !"), )"., 23 1 !")) "1 & #&, ". 7 $ &, - 2 . !$ $# $, !")) "2 ' $6(("*" ' hk , $ $ $ & 7% -" &! % $ .'& !1 & '). $ % !"), ' !$&- % 0 ! & #&, )"$ 3", .,"2"1 ,0% 0 !1 ! 2 & $ $ -$ 1% .
#&, «) !" ! 1 3,1- » !")) "2 , !- & #&, - %! &-
, $,/ $ % #! &" ,/ $# 2 ! /0 " +$ $3$ ,$ ,".$& -$ 2 ! $ , , - &$# " - &'# )$) ' & #&, & ' ,0. $ % ,"." 04 1 ( *"1 ") &"%
|
2 |
|
π − |
1 |
(1− t 2 ) e− |
t 2 |
(84) |
|
ψ (t) = |
|
4 |
2 . |
|||||
|
|
|
||||||
|
|
|||||||
3 |
|
|
|
|
|
|||
- / 6 $ $ & #&, E7 , -$6 $) $ ") &'!$ $ . 3 -
" . +$ $3$ - "!-$!$ , %,1 ,". !,$7 '+ !" ,$& " & %& +) -$) !, 2 2 ! $ "!-$,/. !1 %,1 ,". ".$ $- '+ -$, #.
;" $ $ !- $! " -$, 2", & #&, $ ,
|
t} e− |
t 2 |
|
(85) |
ψ (t) = exp{ jω |
2 |
, |
||
0 |
|
|
|
|
% ω0 – %$)" 1 2 ! $ , -$.&$,104 1 & /" $& / ". " ,/ $! /
."! . 9 $ & #&, $ ,"2 $ % "+, - 7% &! $, $, 2 $ $ 1&,1 !1$)-, ! $# ( *" #, $ $ $# & 4 ! & ' " ) ")' 2 ! " – )$% - ," $& ' !!" $# )$ " ".
