Основы физической химии_Ерёмин
.pdf
258 |
Г л а в а 4. Статистическая термодинамика |
16-2. Рассчитайте поступательный вклад в энтропию газообразного кислорода при температуре –10 °С и давлении 1.1 атм.
16-3. Рассчитайте вращательный вклад в энтропию оксида углерода (II) при температуре 200 °С. Вращательная постоянная CO: B = 1.93 см–1.
16-4. Рассчитайте вращательный вклад в энтропию бромоводорода при температуре 100 °С. Вращательная постоянная B = 8.47 см–1.
16-5. Поступательный вклад в энтропию водорода при некоторых условиях равен 108.0 Дж моль–1 К–1, а в энтропию неизвестного газа при этих же условиях 147.1 Дж моль–1 К–1. Определите неизвестный газ.
16-6. Вращательный вклад в энтропию CO при некоторой температуре равен 51.5 Дж моль–1 К–1. Чему равен вращательный вклад в энтропию
O2 при этой температуре? Вращательные постоянные: CO – 1.93 см–1, O2 – 1.45 см–1.
16-7. Вращательный вклад в энтропию CO при температуре 500 К равен 51.5 Дж моль–1 К–1. Чему равен этот вклад при комнатной температуре
(293 К)?
16-8. Вращательный вклад в энтропию некоторого газа (молекула – линейная) при комнатной температуре (293 К) равен 33.7 Дж моль–1 К–1. Чему равен этот вклад при температуре 450 К?
16-9. Рассчитайте колебательный вклад в энтропию и изохорную теплоемкость газообразного фтора (ω = 917 см–1) при температурах 298 и 1273 К.
16-10. Рассчитайте молекулярную вращательную сумму по состояниям и вращательные вклады в мольные энтропию и изохорную теплоем-
кость для молекулярного фтора при 298 и 1273 K. Вращательная посто-
янная F2: B = 0.89 см–1.
16-11. Составьте программу расчета вращательной суммы по состояниям и вращательного вклада в термодинамические функции для линейной молекулы при произвольных температурах. Используя численный расчет, постройте график зависимости вращательного вклада в изохорную теплоемкость HCl (B = 10.59 см–1) от температуры и покажите, что эта функция имеет максимум.
16-12. Рассчитайте поступательную сумму по состояниям и поступательные вклады в мольные энтропию и изохорную теплоемкость для молекулярного фтора при 298 и 1273 K (давление 1 атм).
16-13. Рассчитайте мольные энтропию, внутреннюю энергию, энтальпию, энергии Гельмгольца и Гиббса газообразного аргона при T = 298 K и давлении 1 атм.

Г л а в а 4. Статистическая термодинамика |
259 |
16-14. Рассчитайте мольную энтропию H35Cl при давлении 10 атм и температуре 500 К, если rHCl = 0.127 нм, ω = 2989 см–1.
16-15. Рассчитайте мольные энтропию, внутреннюю энергию, энтальпию, энергии Гельмгольца и Гиббса газообразного молекулярного иода при T = 500 K и давлении 5 атм. Вращательная постоянная B = 0.0374 см–1, частота колебаний ω = 214 см–1.
16-16. Оцените мольные теплоемкости Cp газообразных CO и этилена при комнатной температуре.
16-17. Оцените мольные теплоемкости CV газообразных HCl и NO2 при комнатной температуре.
16-18. Сравните мольные теплоемкости газообразных воды и углекислого газа при 300 K в предположении, что вкладами электронных и колебательных движений можно пренебречь.
16-19. Не проводя вычислений, сравните теплоемкости CV оксида азота N2O и оксида углерода CO2 при 298 K с использованием следующих молекулярных постоянных:
молекула |
основное |
частоты колебаний (см–1) |
вращ. пост. |
||
состояние |
ν1 |
ν2 |
ν3 |
B (см–1) |
|
CO2 |
X 1 Σ +g |
1334 |
667(2) |
2350 |
0.390 |
N2O |
X 1 Σ +g |
1277 |
588(2) |
2223 |
0.419 |
16-20. Основной вклад в изохорную теплоемкость кристаллических веществ вносят колебания кристаллической решетки. Считая, что кристаллическое вещество представляет собой совокупность 3NA гармонических осцилляторов с одинаковой частотой ω, рассчитайте его мольную изохорную теплоемкость и энтропию при высоких температу-
рах (T >> Tкол).
16-21. Рассчитайте электронный вклад в мольную изохорную теплоемкость газообразного NO при T = 300 К. Разность энергий основного и первого возбужденного электронных состояний равна 120 см–1, статистические веса электронных состояний: g0 = 2, g1 = 4.
16-22. У какого из газов – кислорода или водорода – больше энтропия при одинаковых условиях? Объясните, почему.
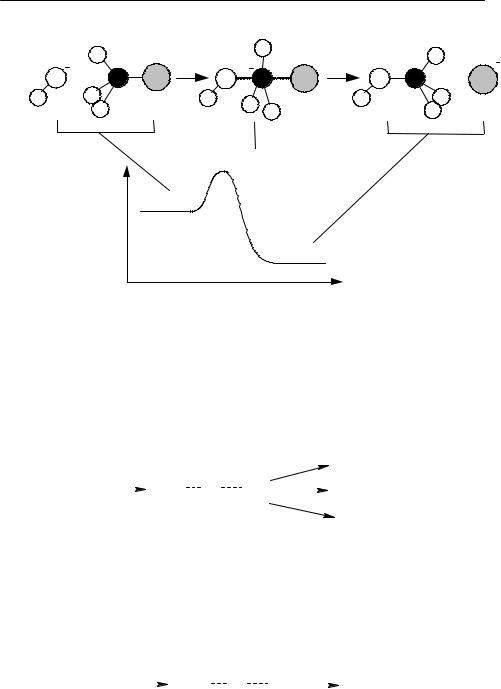
16-23. Рассчитайте константу равновесия Kp для реакции диссоциации: AlCl = Al + Cl при 2000 K. Молекулярные постоянные AlCl: ω = 479 см–1, B = 0.24 см–1, g0 = 1. Основные электронные состояния атомов алюминия и хлора двукратно вырождены. Энергия диссоциации D0 = 119 ккалмоль–1. Возбужденными электроннымисостояниямипренебречь.

260 |
Г л а в а 4. Статистическая термодинамика |
16-24. Рассчитайте константу равновесия Kp для реакции N2 + O2 = 2NO при температуре 600 K. Молекулярные постоянные:
|
ω, см–1 |
B, см–1 |
g0 |
N2 |
2358.0 |
2.00 |
1 |
NO |
1904.4 |
1,705 |
4 |
O2 |
1579.8 |
1.447 |
3 |
Теплота реакции при абсолютном нуле: ∆U0° = 180.3 кДж моль–1. Возбужденными электронными состояниями пренебречь.
16-25. Рассчитайте константу равновесия Kp для реакции
H2 + Cl = HCl + H
при T = 500 К. Молекулярные постоянные:
|
ω, см–1 |
|
B, см–1 |
g0 |
Н2 |
4405 |
60.86 |
1 |
|
HCl |
2991 |
10.59 |
1 |
|
Основное состояние атома водорода вырождено двукратно, атома хлора – четырехкратно. Теплота реакции при абсолютном нуле: ∆U0° = –184.3 кДж моль–1. Возбужденными электронными состояниями пренебречь.
16-26. Рассчитайте константу равновесия Kp для реакции
H2 (газ) + I2 (газ) = 2HI (газ)
при T = 700 К. Моменты инерции молекул H2 , I2 , HI равны соответственно 0.459 10–47, 749 10–47, 4.31 10–47 кг м2, а колебательные волновые числа – 4405, 214, 2309 см–1. Теплота реакции при абсолютном нуле: ∆U0° = –8.2 кДж моль–1. Возбужденными электронными состояниями пренебречь.
16-27. Покажите, что константа равновесия Kp для реакций изотопного обмена типа
HCl + DBr = DCl + HBr
стремится к 1 при достаточно высоких температурах.
16-28. Предполагая, что водород и гелий описываются уравнением Ван- дер-Ваальса, найдите параметры потенциала Сазерленда (при m = 6) для этих газов. Считайте, что в области притяжения |u(r)| << kT. Параметры уравнения Ван-дер-Ваальса – см. в Приложении.
16-29. Используя решение задачи 15-28, выведите термическое уравнение состояния и найдите второй вириальный коэффициент для решеточного газа с взаимодействием.
Г л а в а 4. Статистическая термодинамика |
261 |
16-30. Вычислите второй вириальный коэффициент и найдите уравнение состояния газа с межмолекулярным взаимодействием в виде прямоугольной потенциальной ямы:
∞, 0 ≤ r < σ u(r) = −ε, σ ≤ r ≤ aσ .
0, r > aσ
16-31. Пользуясь выражением (16.26), докажите, что если межмолекулярный потенциал неотрицателен, то второй вириальный коэффициент B2(T) с ростом температуры монотонно убывает.
16-32. Пользуясь выражением (16.26), докажите, что второй вириальный коэффициент B2(T) как функция температуры может иметь не более одного экстремума.
16-33. Используя статистический подход, получите уравнение изотермы адсорбции смеси двух идеальных газов на однородной поверхности (см. (10.12)).
16-34. С помощью статистической термодинамики выведите уравнение изотермы адсорбции реального, сильно разреженного газа. Воспользуйтесь конфигурационным интегралом (15.59).

Глава 5 Химическая кинетика
§ 17. Основные понятия химической кинетики
С помощью химической термодинамики можно определить направление любой химической реакции при заданных условиях. Термодинамика, однако, ничего не может сказать о том, осуществима ли данная реакция и за какое время она закончится. Например, смесь газообразных водорода и кислорода термодинамически неустойчива и должна самопроизвольно превращаться в воду, однако без внешнего воздействия и в отсутствие катализатора водород с кислородом практически не будут реагировать даже в течение миллионов лет. Время в химию вво-
дит химическая кинетика.
Химическая кинетика – раздел физической химии, изучающий скорости химических реакций. Основные задачи химической кинетики:
1)расчет скоростей реакций и определение кинетических кривых, т.е. зависимости концентраций реагирующих веществ от времени
(прямая задача);
2)определение механизмов реакций по кинетическим кривым (обрат-
ная задача).
Основные различия между химической термодинамикой и кинетикой:
1.В химической термодинамике нет времени, она предсказывает только конечный результат процесса. Химическая кинетика изучает только изменяющиеся (динамические) системы.
2.Равновесные свойства определяется состоянием как исходных веществ, так и продуктов реакции. Для термодинамики важны левая и правая части химического уравнения. Скорость реакции определяется только состоянием исходных веществ. Для кинетики важна только левая часть уравнения реакции.