
- •2.1Свойства операций над векторами.
- •2,2 Линейная зависимость и независимость векторов.
- •Геометрическая интерпретация скалярного произведения.
- •Свойства смешанного произведения:
- •Угол между двумя прямыми
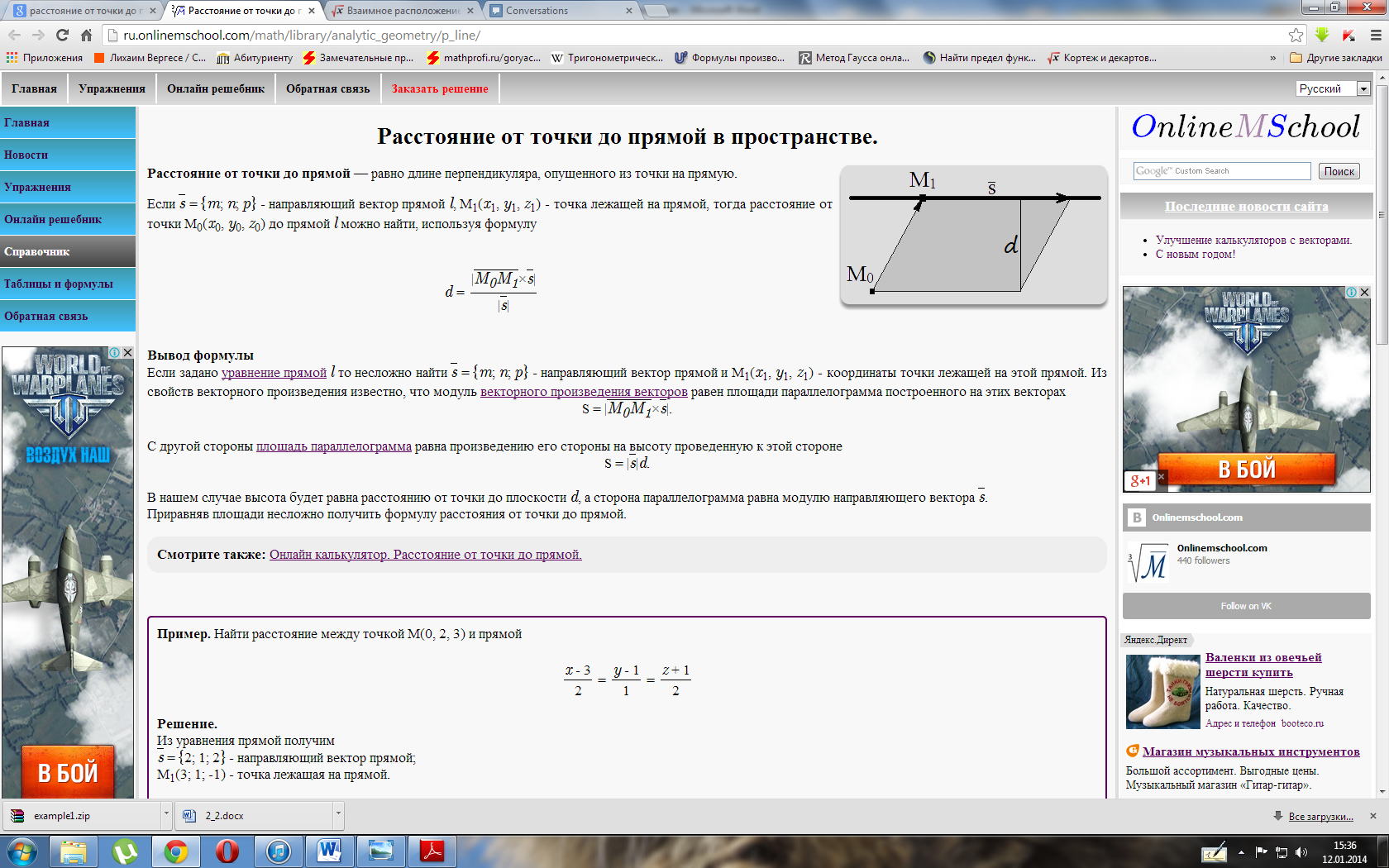
- •Расстояние от точки до прямой
- •Уравнение плоскости, проходящей через данную точку перпендикулярно данному вектору
- •Общие уравнения прямой в пространстве
- •Взаимное расположение прямой и плоскости в пространстве.
- •Проекция точки на плоскость
Общие уравнения прямой в пространстве
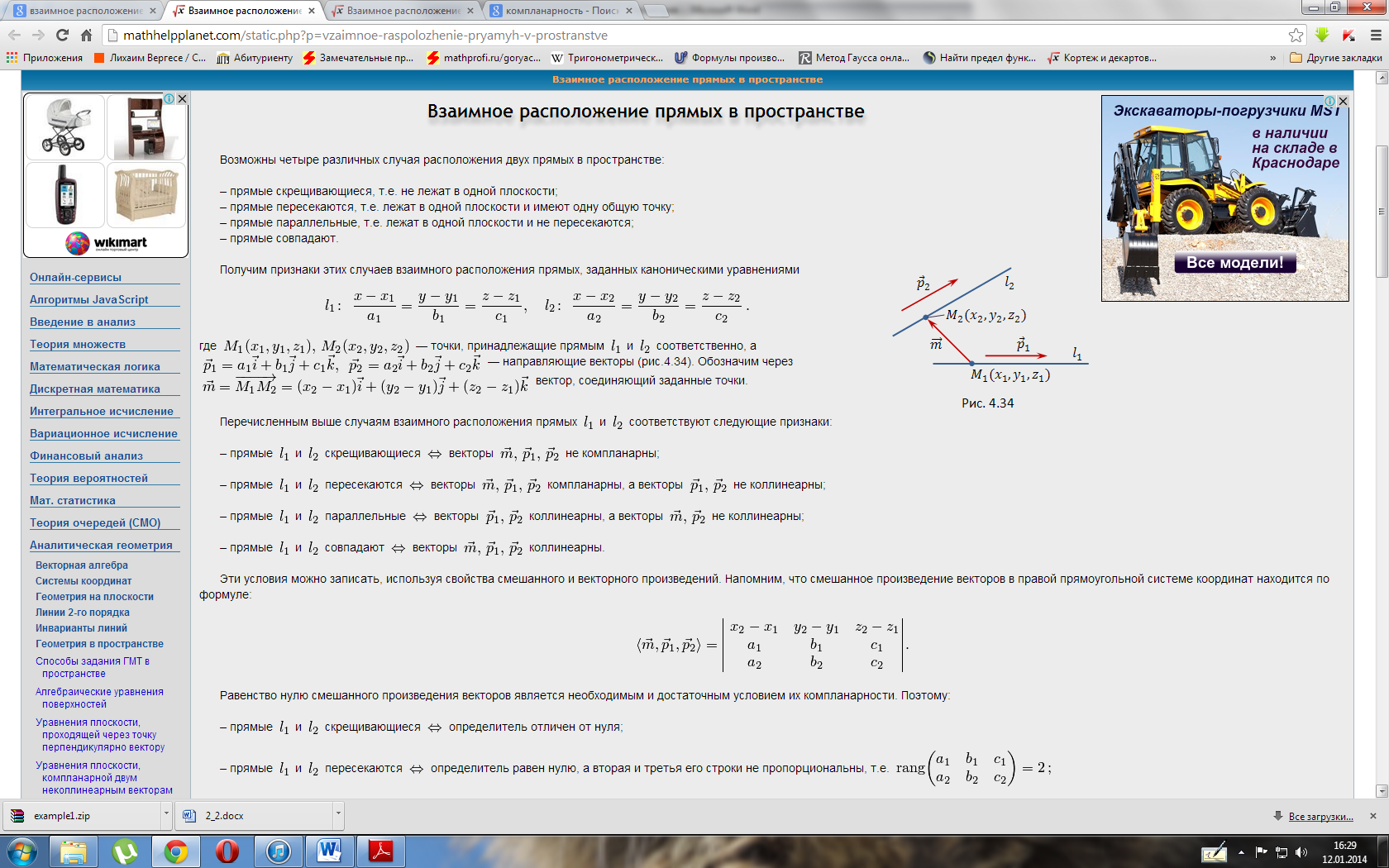
Линия в трехмерном пространстве определяется, вообще говоря, пересечением двух поверхностей, т.е. описывается системой двух уравнений.
Прямую в пространстве можно рассматривать как линию пересечения двух плоскостей и, следовательно, описывать системой двух линейных уравнений
|
|
м н о |
|
|
| ||
|
|
|
|
при условии, что эти плоскости непараллельны, т.е. их нормальные векторы неколлинеарны.
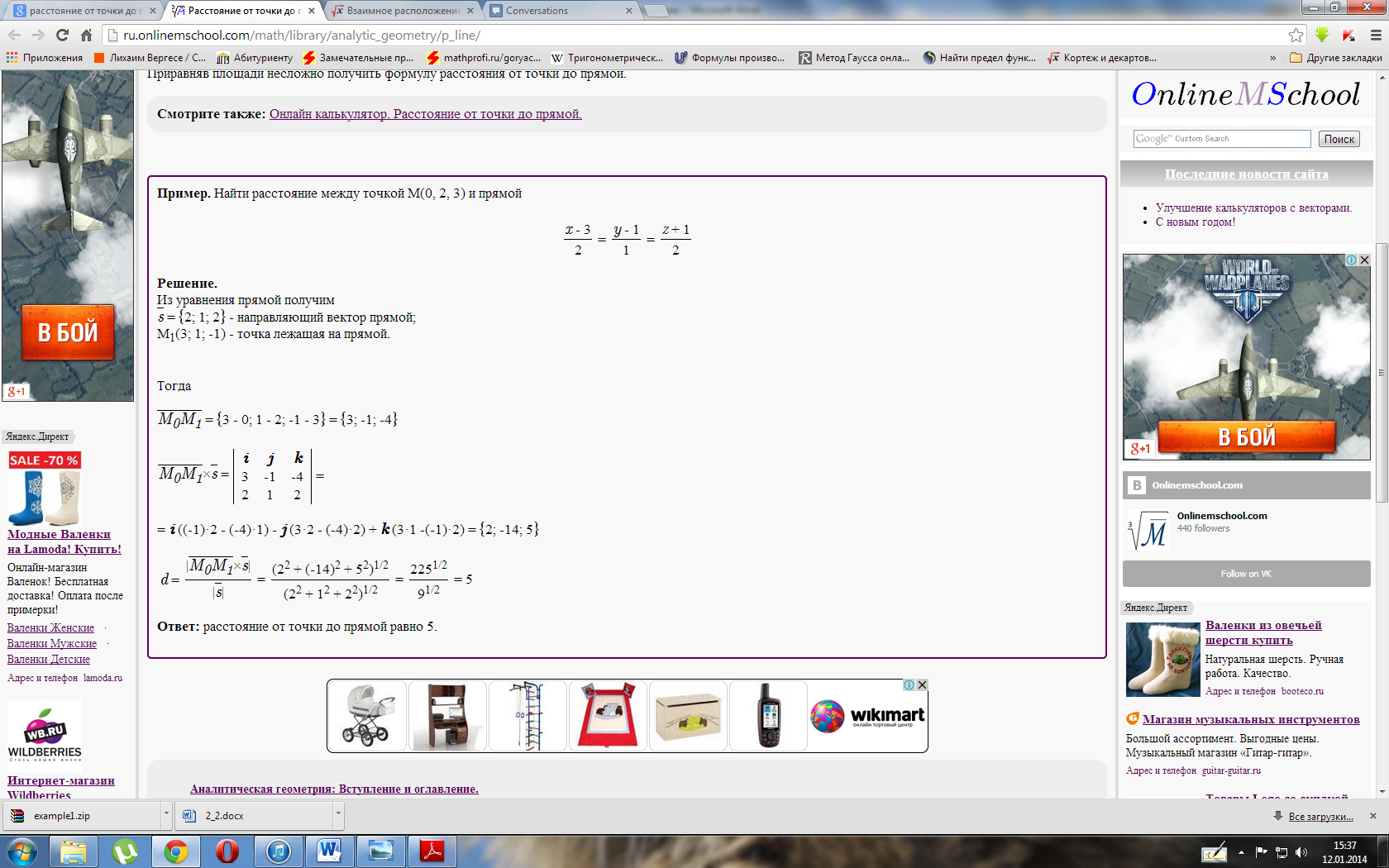
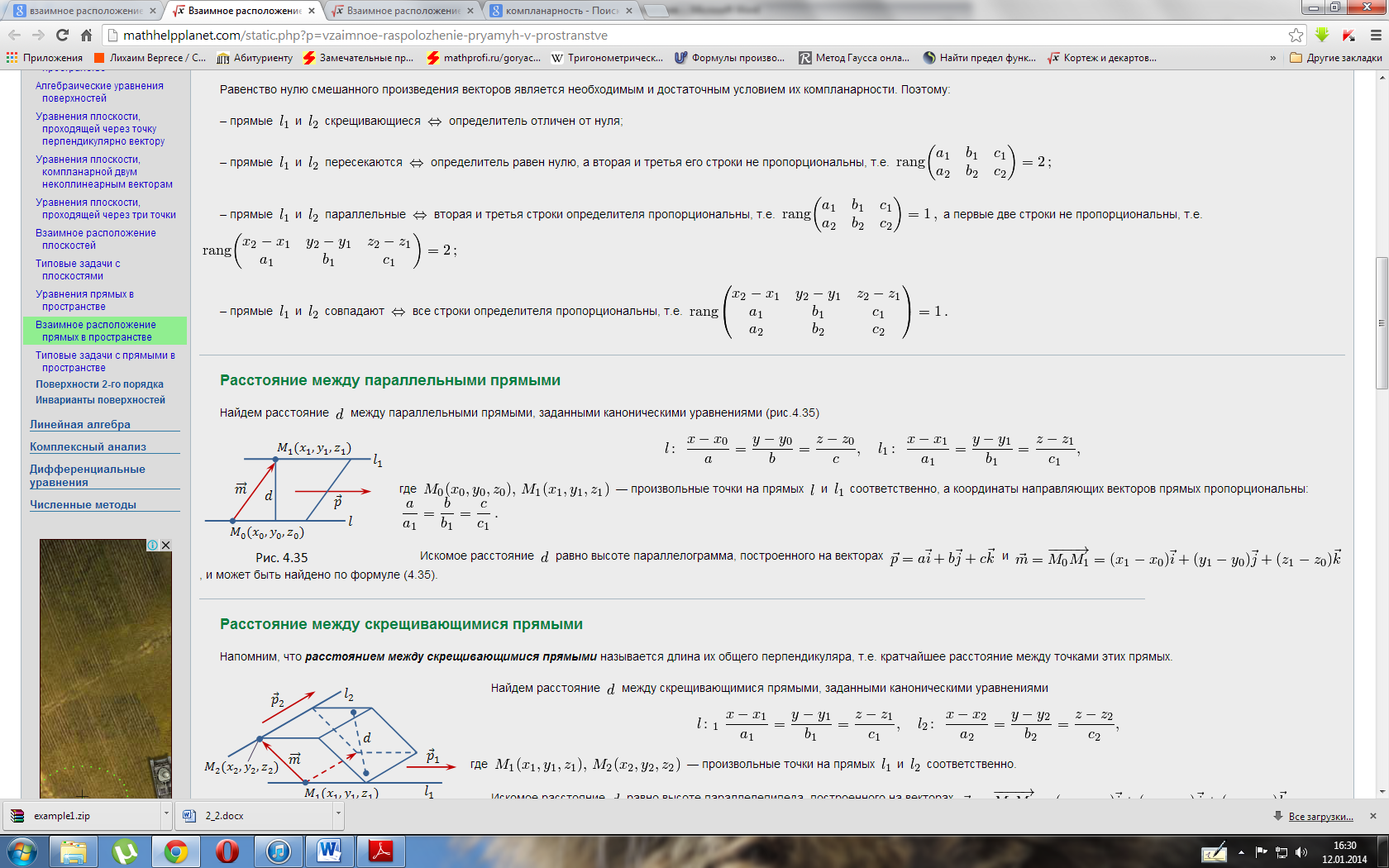
Расстояние между скрещивающимися прямыми в пространстве
В трехмерном пространстве в прямоугольной системе координат Oxyz заданы две скрещивающиеся прямые a и b. Прямую a определяют параметрические уравнения прямой в пространствевида
X=-2
Y=2t+1
Z=-3t+4
,
а прямую b – канонические
уравнения прямой в пространстве![]() .
Найдите расстояние между заданными
скрещивающимися прямыми.
.
Найдите расстояние между заданными
скрещивающимися прямыми.
Очевидно,
прямая a проходит через точку ![]() и
имеет направляющий вектор
и
имеет направляющий вектор![]() .
Прямая b проходит через точку
.
Прямая b проходит через точку![]() ,
а ее направляющим вектором является
вектор
,
а ее направляющим вектором является
вектор![]() .
.
Вычислим
векторное произведение векторов ![]() и
и![]() :
: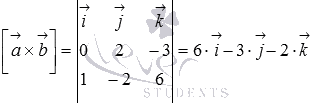
Таким
образом, нормальный вектор  плоскости
плоскости![]() ,
проходящей через прямую b параллельно
прямой a, имеет координаты
,
проходящей через прямую b параллельно
прямой a, имеет координаты![]() .
.
Тогда
уравнение плоскости ![]() есть
уравнение плоскости, проходящей через
точку
есть
уравнение плоскости, проходящей через
точку![]() и
имеющей нормальный вектор
и
имеющей нормальный вектор![]() :
:![]()
Нормирующий
множитель для общего уравнения
плоскости ![]() равен
равен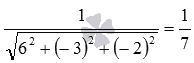 .
Следовательно, нормальное уравнение
этой плоскости имеет вид
.
Следовательно, нормальное уравнение
этой плоскости имеет вид![]() .
.
Осталось
воспользоваться формулой для вычисления
расстояния от точки ![]() до
плоскости
до
плоскости![]() :
:![]()
Это и есть искомое расстояние между заданными скрещивающимися прямыми.
Взаимное расположение прямой и плоскости в пространстве.
Теорема.
Пусть плоскость ![]() задана
общим уравнением
задана
общим уравнением
![]() ,
,
а прямая L задана каноническими уравнениями
![]()
или параметрическими уравнениями
 ,
, ![]() ,
,
в
которых ![]() – координаты нормального вектора плоскости
– координаты нормального вектора плоскости ![]() ,
, ![]() – координаты произвольной
фиксированной точки прямой L,
– координаты произвольной
фиксированной точки прямой L, ![]() –
–
координаты направляющего вектора прямой L. Тогда:
1)
если ![]() ,
то прямая L пересекает плоскость
,
то прямая L пересекает плоскость ![]() в
точке,координаты которой
в
точке,координаты которой ![]() можно
найти из системы уравнений
можно
найти из системы уравнений
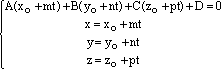 ;
(7)
;
(7)
2)
если ![]() и
и ![]() ,
то прямая лежит на плоскости;
,
то прямая лежит на плоскости;
3)
если ![]() и
и ![]() ,
то прямая параллельна плоскости.
,
то прямая параллельна плоскости.
Доказательство.
Условие ![]() говорит
о том, что вектроры
говорит
о том, что вектроры ![]() и
и ![]() не
ортогональны, а значит прямая не
параллельна плоскости и не лежит в
плоскости, а значит пересекает ее в
некоторой точке М. Координаты точки
М удовлетворяют как уравнению плоскости,
так и уравнениям прямой, т.е. системе
(7). Решаем первое уравнение системы (7)
относительно неизвестной t и затем,
подставляя найденное значение t в
остальныеуравнения системы,
находим координаты искомой
точки.
не
ортогональны, а значит прямая не
параллельна плоскости и не лежит в
плоскости, а значит пересекает ее в
некоторой точке М. Координаты точки
М удовлетворяют как уравнению плоскости,
так и уравнениям прямой, т.е. системе
(7). Решаем первое уравнение системы (7)
относительно неизвестной t и затем,
подставляя найденное значение t в
остальныеуравнения системы,
находим координаты искомой
точки.
Если ![]() ,
то это означает, что
,
то это означает, что ![]() .
А такое возможно лишь тогда, когда прямая
лежит на плоскости или параллельна ей.
Если прямая лежит на плоскости, то любая
точка прямой является точкой плоскости
икоординаты любой
точки прямой удовлетворяют уравнению
плоскости. Поэтому достаточно проверить,
лежит ли на плоскости точка
.
А такое возможно лишь тогда, когда прямая
лежит на плоскости или параллельна ей.
Если прямая лежит на плоскости, то любая
точка прямой является точкой плоскости
икоординаты любой
точки прямой удовлетворяют уравнению
плоскости. Поэтому достаточно проверить,
лежит ли на плоскости точка ![]() .
Если
.
Если ![]() ,
то точка
,
то точка ![]() –
лежит на плоскости, а это означает, что
и сама прямая лежит на плоскости.
–
лежит на плоскости, а это означает, что
и сама прямая лежит на плоскости.
Если ![]() ,
а
,
а ![]() ,
то точка на прямой не лежит на плоскости,
а это означает, что прямая параллельна
плоскости.
,
то точка на прямой не лежит на плоскости,
а это означает, что прямая параллельна
плоскости.
Угол между прямой и плоскостью в пространстве
Угол ψ между прямой K (с направляющими коэффициентами l, m, n) и плоскостью
Ах+By+Cz+D=0 находится по формуле:
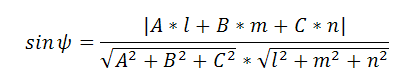
Пример.
Найти угол между прямой ![]() и
плоскостью
и
плоскостью![]() .
.
Решение.
По условию ![]() ,
,![]() ,
тогда
,
тогда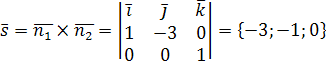 .
.
Из
уравнения плоскости имеем, что нормальный
вектор ![]() .
Следовательно
.
Следовательно![]() =
=![]()
![]() .
.
