- •Министерство образования, науки и молодежной политики Забайкальского края
- •Тематический план и график срс
- •Введение
- •Раздел 1. Развитие и понятие о числе Самостоятельная работа № 1
- •Теоритическое обоснование:
- •Текст задания:
- •Самостоятельная работа № 2
- •Теоритическое обоснование: Определение комплексного числа
- •Геометрическое изображение суммы и разности комплексных чисел.
- •Текст задания:
- •Раздел 2. Корни, степени, логарифмы. Функции, их свойства и графики.
- •Текст задания:
- •Текст задания:
- •Самостоятельная работа № 7
- •Текст задания:
- •Самостоятельная работа № 9
- •Теоритическое обоснование:
- •Текст задания:
- •Самостоятельная работа № 12
- •Теоритическое обоснование:
- •Текст задания:
- •Самостоятельная работа №13
- •Теоритическое обоснование:
- •Текст задания:
- •Раздел 5. Прямые и плоскости в пространстве Самостоятельная работа № 14
- •Теоритическое обоснование:
- •Текст задания:
- •Самостоятельная работа № 15
- •Теоритическое обоснование:
- •Текст задания:
- •Раздел 6. Многогранники Самостоятельная работа № 16
- •Теоритическое обоснование:
- •Текст задания:
- •Раздел 7. Тела и поверхности вращения Самостоятельная работа № 17
- •Текст задания:
- •Самостоятельная работа № 18
- •Теоритическое обоснование: Шар (сфера) и плоскость
- •Текст задания:
- •Раздел 8. Координаты и векторы Самостоятельная работа № 19
- •Теоритическое обоснование:
- •Текст задания:
- •Самостоятельная работа № 20
- •Теоритическое обоснование:
- •Текст задания:
- •Элементы комбинаторики, статистики и теории вероятностей
- •Определение 1. Размещением из n элементов по m в комбинаторике называется любой упорядоченный набор из m различных элементов, выбранных из генеральной совокупности в n элементов.
- •Число сочетаний из n элементов по m
- •Текст задания:
- •Самостоятельная работа № 22
- •Теоритическое обоснование:
- •Текст задания:
- •Самостоятельная работа № 23
- •Теоритическое обоснование: Связь математической статистики с теорией вероятностей.
- •Текст задания:
- •Литература
- •Содержание
- •Бронников Анатолий Павлович математика
Текст задания:
Вычислите
логарифмы с использованием следующих
формул:
![]() и
и![]()
1) ![]()
2) ![]()
3) ![]()
4) ![]()
5) ![]()
6) ![]()
7) ![]()
8) ![]()
9) ![]()
10) ![]()
11) ![]()
12) ![]()
13) ![]()
Задачи
на основное логарифмическое тождество: ![]()
1) ![]()
2) ![]()
3) ![]()
4) ![]()
5) ![]()
6) ![]()
7) ![]()
8) ![]()
9) ![]()
10) ![]()
11) ![]()
12) ![]()
13) ![]()
14) ![]()
15) ![]()
16) ![]()
17) ![]()
Задачи
на формулу перехода к новому основанию
![]()
1) ![]()
2) ![]()
3) ![]()
4) 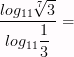
5) ![]()
6) 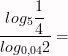
7) ![]()
8) ![]()
9) ![]()
Раздел 3. Основы тригонометрии. Функции, их свойства и графики.
Уравнения и неравенства
Самостоятельная работа № 6
Тема: Формулы половинного аргумента
Цель: закрепить знания и умения студентов применять основные тригонометрические формулы.
Теоритическое обоснование:
Формулы половинного аргумента
Синус половинного угла
![]()
Примечание: Знак перед корнем выбирается в зависимости от квадранта, в который попадает угол α/2 в левой части. Данное правило справедливо также для других формул, приведенных ниже.
Косинус половинного угла
![]()
Тангенс половинного угла
![]()
Котангенс половинного угла
![]()
Выражение синуса через тангенс половинного угла
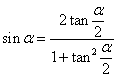
Выражение косинуса через тангенс половинного угла
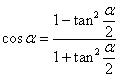
Выражение тангенса через тангенс половинного угла
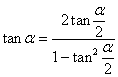
Выражение котангенса через тангенс половинного угла
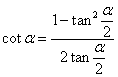
Текст задания:
1. Доказать тождества :
а). 1 + 2 cos 2α + cos 4α = 4 cos2 α cos 2α.
б). 1 — 2 cos 3α + cos 6α = — 4 sin2 3α/2 • cos 3α.
в). 1 + sin α = 2cos2 (π/4 — α/2).
г). 1— sin α = 2sin2 (π/4 — α/2).
2. Упростить
выражение ![]()
3. Найти sin α, cos α и tg α, если известно, что cos 2α = —0,6.
4. Найти sin α/2, cos α/2 и tg α/2, если известно, что | cos α | = 0,6, причем угол α, оканчивается во 2-й четверти,
5. Найти tg α, если sin 2α = 1/3.
6. Вычислить:
а). sin ( 1/2 arccos 0,8 ). в). tg [ 1/2 arcsin (— 0,8 )]
б). cos ( 1/2 arcsin 0,6 ) г). tg [ 1/2 arctg (— 0,75 )]
Самостоятельная работа № 7
Тема: Преобразование тригонометрических выражений
Цель: закрепить знания и умения студентов по освоению свойств тригонометрических функций.
Теоритическое обоснование:
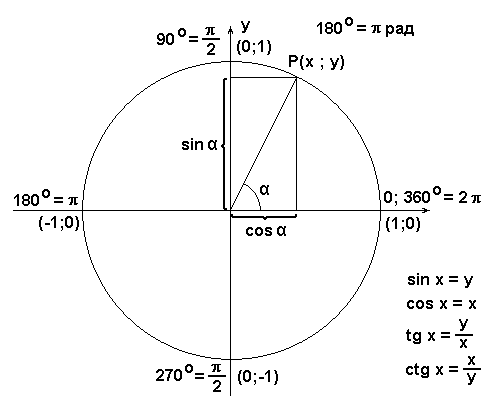
Формулы приведения:
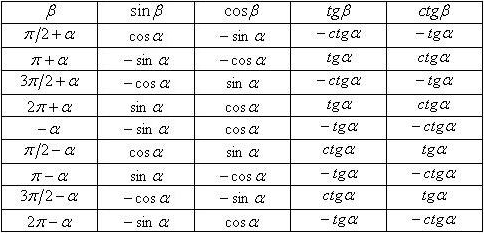

Текст задания:
1.
Найти значение выражения ![]() ,
если известно, что tg α = 1/3
,
если известно, что tg α = 1/3
2.
Найти значение выражения ![]() ,
если известно, что котангенс угла α не
определен.
,
если известно, что котангенс угла α не
определен.
3.
Найти значение выражения ![]() ,
если известно, что ctg α = ½
,
если известно, что ctg α = ½
4. Упростить выражения:

5. Доказать тождества:
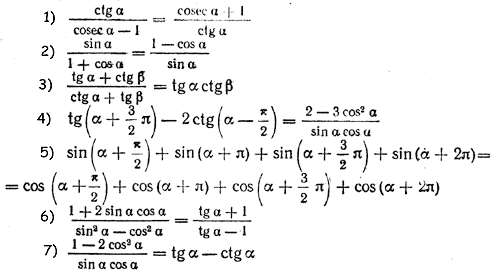
Самостоятельная работа № 8
Тема: Решение тригонометрических неравенств (синус, косинус).
Цель: закрепить знания и умения студентов по освоению методов решения тригонометрических неравенств.
Теоритическое обоснование:
Утверждение 1. Множество решений неравенства sinx > a, есть
R, если a < -1;
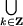 (arcsina +
2pk; p -
arcsina +
2pk),
если
-1 ≤ a <
1;
(arcsina +
2pk; p -
arcsina +
2pk),
если
-1 ≤ a <
1;Пустое множество, если a ≥ 1.
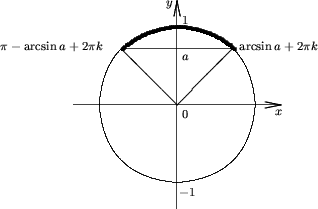
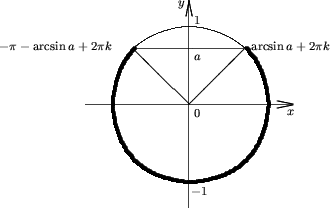
Утверждение 2. Множество решений неравенства sinx < a, есть
R, если a > 1;
 (-p -
arcsina +
2pk;
arcsina +
2pk),
если
-1 < a ≤
1;
(-p -
arcsina +
2pk;
arcsina +
2pk),
если
-1 < a ≤
1;Пустое множество, если a ≤ -1.
Утверждение 3. Множество решений неравенства cosx > a, есть
R, если a < -1;
 (2pk -
arccosa;
2pk +
arccosa),
если
-1 ≤ a <
1;
(2pk -
arccosa;
2pk +
arccosa),
если
-1 ≤ a <
1;Пустое множество, если a ≥ 1.
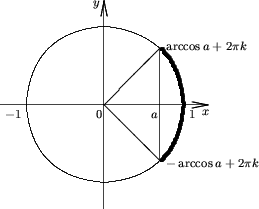
Утверждение 4. Множество решений неравенства cosx < a, есть
|
|
|
R, если a > 1;
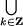 (2pk +
arccosa;
2p(k +
1) - arccosa),
если
-1 < a ≤
1;
(2pk +
arccosa;
2p(k +
1) - arccosa),
если
-1 < a ≤
1;Пустое множество, если a ≤ -1.