Теория массового обслуживания (ТМО) / Конспект лекций по ТМО / TEMA5~1

Одноканальная СМО с ожиданием и ограничением на длину очереди

Рассмотрим СМО с одним каналом (п = 1), на вход которой поступает простейший поток заявок с интенсивностью . Предположим, что поток обслуживании также простейший с интенсивностью . Это означает, что непрерывно занятый ка­нал обслуживает в среднем  заявок в единицу времени. Заяв­ка, поступившая в СМО в момент, когда канал занят, в отли­чие от СМО с отказами, не покидает систему, а становится в очередь и ожидает обслуживания.

Далее предполагаем, что в данной системе имеется ограни­чение на длину очереди, под которой, напомним, понимается максимальное число мест в очереди, а именно предполагаем, что в очереди могут находиться максимум т >= 1 заявок. Поэто­му заявка, пришедшая на вход СМО, в момент, когда в очереди уже стоят т заявок, получает отказ и покидает систему не обслуженной.

Таким образом, рассматриваемая СМО относится к систе­мам смешанного типа с ограничением на длину очереди.

Пронумеруем состояния СМО по числу заявок, находящих­ся в системе, т.е. под обслуживанием и в очереди:

s₀ — канал свободен (следовательно, очереди нет);

s₁ — канал занят и очереди нет, т.е. в СМО находится (под обслуживанием) одна заявка;

s₂ — канал занят и в очереди стоит одна заявка;

…

S_к — канал занят и в очереди k -1 заявка;

…

S_m+1 - канал занят и в очереди т заявок. Таким образом, СМО может находиться в одном из т + 2 состояний, граф которых представлен на рис. 5.1.

В каждом из состояний S_k, k == 1, ..., т + I, в системе нахо­дится, по сравнению с предыдущим состоянием S_k-1, на одну заявку больше, которая поступает во входящем потоке. Так что переходы СМО из состояния S_k-1 в состояние S_k, k = 1, ..., т + 1, (по стрелкам слева направо) происходят под воздействием входящего потока заявок. А так как этот поток имеет интенсивность, то плотности вероятностей переходов _k-1,k=, k=1,…,m+1

Переходы системы справа налево осуществляются "потоком обслуживании", поскольку в момент окончания обслуживания очередной заявки канал освобождается и либо будет простаи­вать (если в очереди нет заявок), либо примет к обслуживанию заявку из очереди; и в том, и в другом случае число заявок в системе уменьшится на единицу. Поскольку интенсивность потока обслуживании равна , то плотности вероятностей пе­реходов справа налево _k,k-1=, k=1,…,m+1

Расставив у стрелок графа плотности вероятностей перехо­дов, получим размеченный граф состояний данной СМО (см. рис. 5.1), из которого видно, что протекающий в ней процесс является процессом "гибели и размножения".

Обозначив через po(t), р1(t ), ..., pk(t)....,Pm+1(t) (t>= 0) вероят­ности соответствующих состояний системы S0, S1,...,S_k,...,S_m+1 в момент времени t, мы можем по одному из известных правил записать для них систему дифференциальных уравнений Колмогорова:

которая решается при начальных условиях

означающих, что в начальный момент времени t = 0 СМО на­ходилась в состоянии s₀, т.е. канал был свободен.

Поскольку с течением времени установится предельный ре­жим, то нас будут интересовать предельные вероятности со­стояний, которые можно получить из общих формул предельных вероятностей для процесса гибели и разложения (3.19)-(3.21), подстанавливая в них n=m+1; k=1,…,m+1. После подстановки получим:

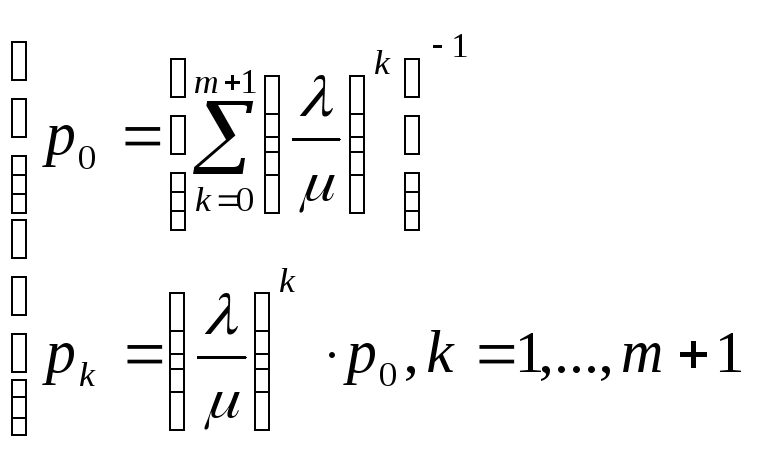
(5.1)

Найденные предельные вероятности состояний удовлетворяют нормировочному условию p0+p1+…+pm+1=1.

В самом деле,

Если , то из формул (5.1) находим, что

p0=p1=…=pm+1= (5.2)

Пусть теперь . Используя приведённую интенсивность входящего потока заявок , из системы (5.1) получим:

(5.3)

причём . Заметим, что представляет собой сумму m+2 членов геометрической прогрессии с первым членом и знаменателем . Тогда по формуле m+2 членов геометрической прогрессии будем иметь:

Подставляем полученное равенство в систему (5.3), получаем:

(5.4)

Формулы (5.2) и (5.4) можно записать в объединенной форме:

(5.5)

Предельные вероятности pk, k=0,1,…,m+1 , можно выра­зить через средний интервал времени T между поступлениями во входящем потоке двух соседних заявок и среднее время об­служивания одной заявки.

Для этого в систему уравнений (5.5) подставим , поскольку

В результате получим:

(5.6)

Найдем предельные характеристики эффективности функ­ционирования СМО:

1) вероятность отказа pотк;

2) вероятность того, что поступившая заявка будет принята в систему (т.е. не получит отказа) р_сис;

3) относительную пропускную способность СМО О;

4) абсолютную пропускную способность СМО А;

5) интенсивность выходящего потока обслуженных заявок v; _

6) среднее число заявок, находящихся в очереди, N _оч;

7) среднее число заявок, находящихся под обслуживанием,

8) среднее число заявок, находящихся в системе (как в очереди, так и под обслуживанием) N _сис;

9) среднее время ожидания заявки в очереди T_оч;

10) среднее время пребывания заявки в системе (как в оче­реди, так и под обслуживанием) Т _сис.

Поступившая на вход СМО заявка получает отказ тогда и только тогда, когда канал занят и в очереди ожидают т заявок, т.е. когда система находится в состоянии 5„+1. Поэтому вероят­ность отказа sm+1 равна вероятности состояния sm+1. Из систе­мы уравнений (5.5) получаем:

(5.7)

Событие, состоящее в том, что поступившая заявка будет принята в систему ( в очередь или под обслуживание), проти­воположно событию, состоящему в отказе заявке. Поэтому ве­роятность принятия заявки в систему p_сис дополняет вероят­ность отказа ротк единицы. Следовательно, из соотношения (5.7):

(5.8)

Так как каждая заявка, принятая в систему (т. е. поступив­шая на вход СМО и не получившая отказ), будет обслужена, то вероятность того, что заявка будет обслужена pоб, совпадает с вероятностью принятия заявки в систему р_сис.

Отметим, что при т = 0 формула (5.8) превращается в фор­мулу (3.24) для вероятности того, что поступившая заявка будет принята к обслуживанию pоб, в случае одноканальной СМО с отказами. -

Относительная пропускная способность системы Q, пред­ставляющая собой среднюю долю принятых в систему заявок среди всех поступивших, равна вероятности того, что посту­пившая заявка будет принята в систему (т.е. не получит отказ):

Абсолютная пропускная способность системы:

(5.9)

Интенсивность выходящего потока Пвых обслуженных заявок

Для нахождения среднего числа заявок, в очереди ,

введем в рассмотрение дискретную случайную величину Nоч представляющую собой число заявок в очереди.

Событие, состоящее в том, что в очереди нет заявок, т.е. что Nоч = 0, является объединением двух несовместных собы­тий: события, состоящего в том, что СМО находится в состоя­нии sо, и события, состоящего в том, что СМО находится в состоянии $1. Поэтому вероятность p(Nоч=0) того, что в очере­ди не будет заявок, равна р0 + р1. Вероятность того, что оче­редь состоит из одной заявки, равна p2 , и т.д.; вероятность наличия т заявок в очереди равна рm+1 . Таким образом, закон распределения случайной величины Nоч, будет иметь вид:

Nоч	0	1		т
р	pо + Р1	p2.	...	Рт+\

Поэтому по определению математического ожидания дискретной случайной величины N_оч с учетом формул (5.5):

(5.10)

Предположим, что р1. Очевидно имеем:

Но сумма представляет собой сумму т членов геометрической прогрессии р, р², р³,..., р^т с первым членом р и знаменате­лем р1. По формуле суммы т членов геометрической про­грессии

Тогда

и из равенства (5.11):

(5.12)

Подставив равенство (5.12) в (5.10), найдем:

или, используя выражение для р0 из системы (5.5) при р1, получим

(5.13)

Если же р = 1, то из равенства (5.10):

(5.14)

По формуле суммы т членов арифметической прогрессии

первым членом а1 = 1 и разностью d =1:

(5.15)

Подставим равенство (5.15) и значение pо при р = 1 из ра­венств (5.5) в (5.14), получим:

(5.16)

Запишем формулы (5.13) и (5.16) в объединенной форме:

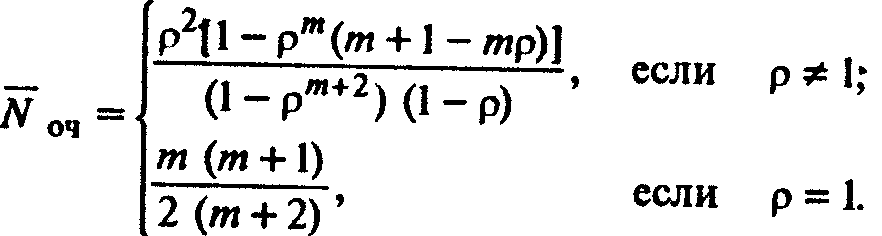
(5.17)

Итак, получено выражение для среднего числа N _оч заявок, стоящих в очереди на обслуживание. Теперь выведем формулу для среднего числа N _сис заявок, находящихся в системе (в оче­реди и под обслуживанием). Для этого рассмотрим дискретную случайную величину Nоб , представляющую собой число заявок, находящихся под обслуживанием. Вследствие того, что рас­сматриваемая СМО одноканальная, случайная величина Nоб может принимать два значения: 0 и 1. Значение Nоб⁼ 0 она принимает с вероятностью ро состояния so, в котором канал свободен. Равенство Nоб = 1 представляет собой событие, со­стоящее в том, что под обслуживанием находится одна заявка, которое противоположно событию, состоящему в том, что ка­нал свободен. Поэтому вероятность того, что Nоб = 1, равна 1 - ро . Таким образом, закон распределения случайной вели­чины Л^₀б выглядит следующим образом:

	Nоб	0	1
	р	p0	1 –p0

и математическое ожидание M|Nоб| случайной величины Nоб , представляющее среднее число заявок под обслуживанием, равно

Подставив сюда выражение ро по формуле (5.5), получим:

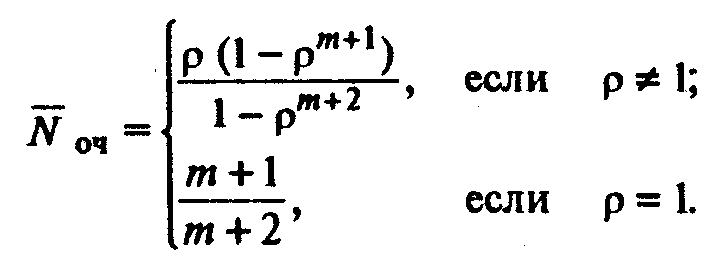
(5.18)

Из сравнения формулы (5.18) с формулами (5.8), (5.9) следует, что

(5.19)

т.е. среднее число заявок, находящихся под обслуживанием, прямо пропорционально относительной пропускной способно­сти , или что то же, вероятности принятия заявки в систему множителем пропорциональности, равным показателю нагрузки (трафику) СМО.

Случайная величина N_сис, представляющая собой число зая­вок, находящихся в СМО, является, очевидно, суммой случай­ных величин N_оч и Nоб, т. е, N_сис = Nоч+ Nоб- Тогда по теореме сложения математических ожиданий среднее число заявок в СМО

(5.20)

Если в формулу (5.20) подставить выражения N _оч и Nоб соответственно по формулам (5.17) и (5.18), то получим:

(5.21)

Важной характеристикой СМО с ожиданием является среднее время ожидания заявки в очереди . Пусть непрерывная случайная величина, представляющая собой время ожидания заявки в очереди. Рассмотрим т + 2 несовместных гипотез Hk , k = 0, 1,..., т + 1, состоящих в том, что СМО нахо­дится соответственно в состояниях sk =0, 1, ..., т + 1. Веро­ятности этих гипотез р(Нk = рk, k=0,1, ..., т+1\.

Если заявка поступает в СМО при гипотезе Но, т.е. когда СМО находится в состоянии , в котором канал свободен, то заявке не придется стоять в очереди и, следовательно, условное математическое ожидание М[Т_оч|Но] случайной величины Т_оч при гипотезе Hо, совпадающее со средним временем ожидания заявки в очереди при гипотезе Hо, равно нулю.

Для заявки, поступившей в СМО при гипотезе Н1, т.е. когда ,СМО находится в состоянии , в котором канал занят, но оче­реди нет, условное математическое ожидание М[Т_ОЧ|Н1] слу­чайной величины Tоч при гипотезе Н1, совпадающее со сред­ним временем ожидания заявки в очереди при гипотезе H1, будет равно среднему времени обслуживания одной заявки

Условное математическое ожидание М[Т_ОЧ|Н2\ случайной величины Tоч при гипотезе H2, т.е. при условии, что заявка поступила в СМО, находящуюся в состоянии , в котором ка­нал занят и в очереди уже ждет одна заявка, равно . И так далее.

Если заявка поступит в систему при гипотезе Нm, т.е. когда канал занят и в очереди ждут т-1 заявок, то М[Т_ОЧ | Hm)=.

Наконец, заявка, пришедшая в СМО при гипотезе Hm+1, т.е. когда канал занят, т заявок стоят в очереди и свободных мест в очереди больше нет, получает отказ и покидает систему. По­этому в этом случае М[Т_ОЧ |Н_т+1]=0.

Следовательно, по формуле полного математического ожи­дания (см. [9], с. 77), среднее время ожидания заявки в очереди

Подставляем сюда выражения , k=1,…,m, по формуле (5.5), получаем:

(5.22)

Если нагрузка , то из равенства (5.22) с учетом формул (5.5), (5.12) и (5.17):

Если же, то подставив в равенство (5.22) выражение р0 по формуле (5.5), значение суммы формуле (5.15), используя формулу (5.17) при и учитывая, что в данном случае будем иметь

Итак, для любого получим формулу Литтла для среднего времени пребывания заявки в очереди:

(5.23)

т.е. среднее время ожидания заявки в очереди Т_оч равно среднему числу заявок в очереди N_оч, деленному на интенсивность X входя­щего потока заявок.

Для вывода формулы среднего времени пребывания заявки в системе Т_сис (как в очереди, так и под обслуживанием) вве­дем в рассмотрение случайную величину T_сис, представляющую собой время пребывания заявки в СМО и являющуюся суммой двух случайных величин

(5.24)

где T_оч - время ожидания заявки в очереди, а - время обслуживания одной заявки.

Случайную величину рассмотрим при двух несовмест­ных гипотезах H_сис и H_отк, состоящих соответственно в том, что поступившая заявка принята в систему для обслуживания и поступившая заявка получает отказ. Вероятности этих гипотез p(Hсис)=pсис и p(Hотк)=pотк. Если заявка поступила в СМО при гипотезе H_сис, то условное математическое ожидание M[|Hсис] случайной величины при гипотезе H_сис будет равно среднему времени обслуживания заявки: М[|H_сис] = . Если же заявка пришла в СМО при гипоте­зе Hотк, то она не обслуживается и потому М[ |H_ОТК] = 0. По формуле полного математического ожидания (см. [9}, с. 77)

Так-как =1/ , и согласно формуле (5.9) p_сис =Q, то

Но из равенства (5.19): . Следовательно,

где -среднее время обслуживания одной заявки, относящееся ко всем заявкам (как обслуженным, так и полу­чившим отказов отличие от среднего времени обслуживания одной заявки =1/ относящегося только к обслуженным заявкам. Таким образом,

(5.25)

т.е. среднее время обслуживания одной заявки, относящееся ко всем заявкам, равно среднему числу заявок, находящихся под обслуживанием, , деленному на интенсивность входящего по­тока заявок.

По теореме сложения математических ожиданий, из равен­ства (5.24) получим:

(5.26)

Подставим сюда выражение и соответственно по формулам (5.23) и (5.25), и учитывая равенство (5.20), получим для рассматриваемой СМО формулу Литтла:

т.е. среднее время нахождения заявки в СМО (в очереди и под об­служиванием) Т_сис равно среднему числу заявок в системе N_сис, деленному на интенсивность входящего потока заявок.

Нетрудно проверить, что при т = 0 формулы (5.1) для ро и p1 превращаются соответственно в формулы (3.17) и (3.18) , а формулы (5.7), (5.8), (5.9) и (5.26) - соответственно в формулы (3.28), (3.24), (3.25) и (3.29) для одноканальной СМО с отказами.

В табл. 5.1. сведены параметры рассматриваемой СМО, в табл. 5.2. — предельные характеристики СМО.

Таблица 5. 1

Параметры одноканальной СМО

с ожиданием и ограничением на длину очереди

№ п/п	Параметры	Обозначения,значения, формулы
1	Число каналов обслуживания
2	Максимальная длина очереди (максимальное число мест в очере­ди)
3	Интенсивность входящего простейшего потока заявок Пвх
4	Производительность канала - ин­тенсивность простейшего потока "обслуживании" Поб (среднее чис­ло заявок, обслуживаемое каналом за единицу времени при непрерыв­ной работе)

Таблица 5.2

Предельные характеристики эффективности

функционирования одноканальной СМО с ожиданием

и ограничением на длину очереди

№ n/n	Предельные характеристики	Обозначения, формулы
1	Показатель на грузки (трафик) системы
2	Вероятности состояний СМО, выраженные через показатель нагрузки
3	Вероятности состояний СМО, выраженные через средний интервал времени между соседними поступающими заявками, и среднее время обслуживания одной заявки.
4	Вероятность отказа
5	Вероятность того, что заявка будет принята в систему(не получит отказ)
6	Относительная пропускная способность СМО
7	Абсолютная пропускная способность СМО
8	Интенсивность выходящего потока заявок
9	Среднее число заявок в очереди
10	Среднее число заявок, находящихся под обслуживанием
11	Среднее число заявок, находящихся в системе(как в очереди, так и под обслуживанием)
12	Среднее время ожидания заявки в очереди
13	Среднее время пребывания заявки в системе(как в очереди, так и под обслуживанием)