Теория массового обслуживания (ТМО) / Конспект лекций по ТМО / TEMA6~1

Однокальная СМО с ожиданием.

Проанализируем работу однокальной СМО с ожиданием без ограничений на длину очереди и на время ожидания в очереди. По прежнему будем предполагать, что входящий поток П_вх с интенсивностью λ и «поток обслуживаний» П_об с интенсивностью μ простейшие.

Такая система представляет собой предельный случай системы, рассмотренной в предыдущем параграфе, при . Таким образом, длина очереди станет бесконечной и в соответствии с этим бесконечным станет число состояний СМО. Размеченный граф состояний представлен на рис. 1.

Рис. 1.

Если , т. е. среднее число заявок, поступивших в систему за единицу времени, больше среднего числа обслуживаемых заявок за то же время при непрерывно работающем канале, то очевидно, что очередь неограниченно растет. В этом случае предельный режим не устанавливается и предельных вероятностей состояний не существует.

В случае только при условии, что входящий поток заявок П_вх и поток обслуживаний П_об регулярные (т. е. заявки поступают в СМО через раные интервалы времени, и время обслуживания одной завки является постоянным, равным интервалу времени между поступлениями заявок), очереди вообще не будет и канал будет обслуживать заявки непрерывно. Но как только входящий поток или поток обслуживаний перестает быть регулярным и приобретает элементы случайности, очередь начинает расти до бесконечности.

Выполнение неравенства означает, что СМО с ожиданием без ограничений на очередь перегружена, т. е. нагрузка на систему , и предельных вероятностей состояний не существует. Поэтому далее в этом параграфе будем предполагать, что , т. е. . При этих условиях с течением времени устанавливается предельный режим и предельные вероятности состояний существуют.

Устремляя m к бесконечности в формулах (5.5) при , получим выражение для предельных вероятностей состояний рассматриваемой СМО:

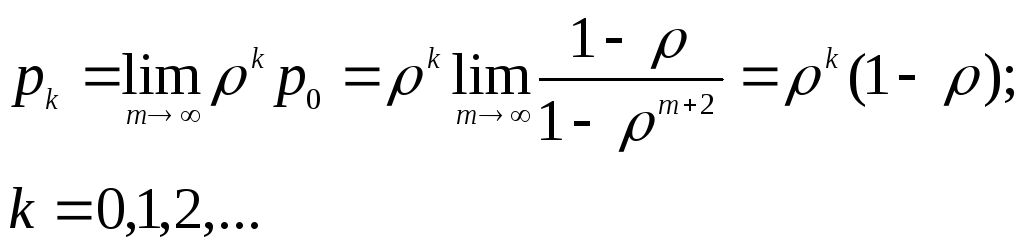(6.1)

Предельные вероятности (6.1) удовлетворяют нормировочному условию p₀ + p₁ + p₂ + … =1. действительно,

Но ряд представляет собой сумму бесконечно убывающей прогрессии с первым членом и знаменателем . По формуле суммы бесконечно убывающей геометрической прогрессии будем иметь:

и, следовательно,

При отсутствии ограничений на очередь каждая заявка, поступившая в СМО, рано или поздно будет обслужена. Поэтому вероятность отказа равна нулю: р_отк = 0.

Следовательно, вероятность того, что поступившая заявка будет принята в систему р_сис, так же как и относительная пропускная способность Q равна единице:

Тогда для абсолютной пропускной способности А и интенсивности выходящего потока П_вых будем иметь:

.

Среднее число заявок в очереди получим из формулы (5.17) при переходом к пределу при :

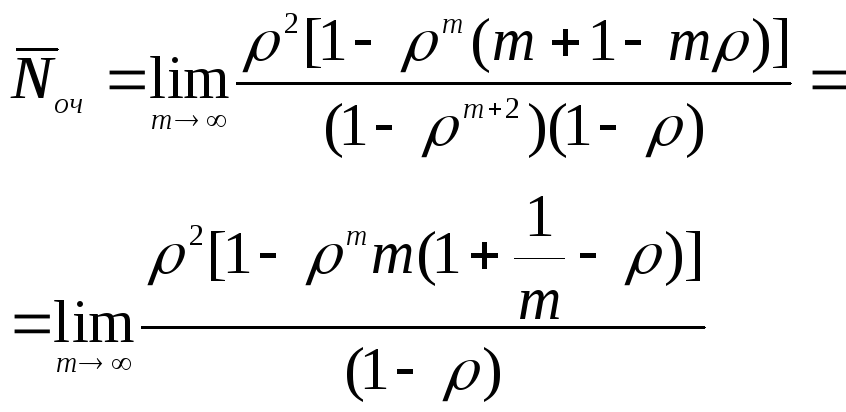
Известно, что бесконечно малая является бесконечно малой высшего порядка, чем бесконечно малая m^-1, т. е. при . Следовательно,

(6.2)

Если в формуле (5.18) при перейти к пределу при , то получим среднее число заявок , находящихся под обслуживанием:

(6.3)

Среднее число заявок в системе (т. е. в очереди и под обслуживанием) можно получить переходя к пределу при в формуле (5.21) при , либо суммируя (6.2) и (6.3):

(6.4)

В формуле Литтла (5.23) среднее число заявок в очереди зависит от длины очереди m (см. формулу (5.17)). Устремляя в формуле (5.23) m к бесконечности, получим в пределе формулу Литтла:

(6.5)

где - среднее время ожидания заявки в очереди для СМО с ожиданием без ограничений на очередь; - среднее число заявок в очереди, вычисляемое по формуле (6.2).

Полученную формулу Литтла (6.5) с учетом формулы (6.2) можно переписать и так:

(6.6)

Наконец, среднее время пребывания заявки в СМО складывается из среднего времени заявки в очереди и среднего времени обслуживания (поскольку для рассматриваемых в этом параграфе систем с ожиданием без ограничений на очередь каждая заявка, поступившая на вход СМО, рано или поздно будет обслужена, то среднее время обслуживания заявки , относящееся ко всем заявкам, совпадает со средним временем обслуживания заявки, относящимся только к обслуженным заявкам: ). Поэтому, воспользовавшись формулой (6.5) и тем, что , получим:

(6.7)

Из формул (6.7) и (6.4) получаем формулу Литтла для среднего времени пребывания заявки в системе:

Эту формулу можно получить и переходом к пределу при в формуле Литтла (5.27).

Параметры и характеристики рассмотренной в этом параграфе СМО представлены в таблице 1 и 2.

Таблица1.

Параметры однокальной СМО с ожиданием

№ п/п	Параметры	Обозначения, значения
1	Число каналов обслуживания	n = 1
2	Максимальная длина очереди (максимальное число мест в очереди)	m = +∞
3	Интенсивность входящего простейшего потока заявок Пвх	in Пвх = λ = const (λ не зависит от времени t)
4	Производительность канала – интенсивность простейшего потока «обслуживаний» Поб (среднее число заявок, обслуживаемое каналом за единицу времени при непрерывной его работе)	in Поб = μ = const (μ не зависит от времени t)
5	Соотношение между λ и μ	λ < μ

Таблица 2.

Предельные характеристики эффективности функционирования однокальной СМО с ожиданием.

№ п/п	Параметры	Обозначения, значения
1	Среднее время обслуживания одной заявки
2	Нагрузка (трафик) системы
3	Вероятности состояний
4	Вероятность отказа	ротк = 0
5	Вероятность того, что заявка будет принята в систему	рсис = 1
6	Относительная пропускная способность СМО	Q = 1
7	Абсолютная пропускная способность СМО	А = λ
8	Интенсивность выходящего потока заявок	ν = λ
9	Среднее число заявок в очереди
10	Среднее число заявок под обслуживанием
11	Среднее число заявок в системе
12	Среднее время ожидания заявки в очереди
13	Среднее время пребывания заявки в системе (как в очереди, так и под обслуживанием)