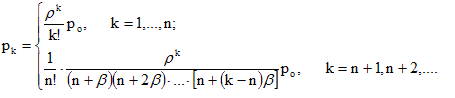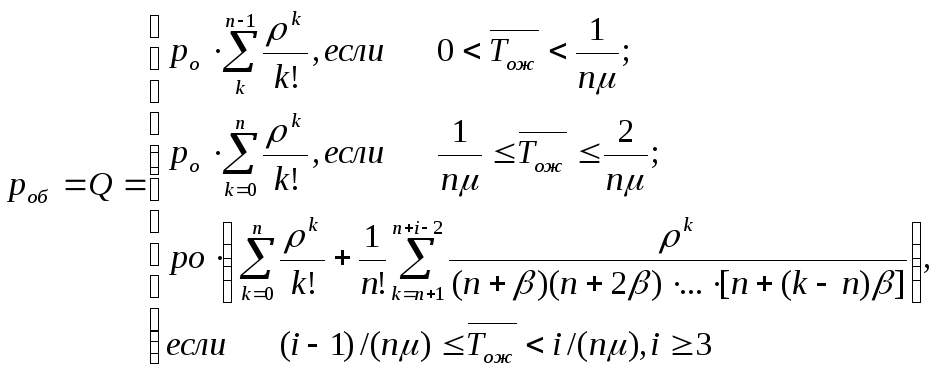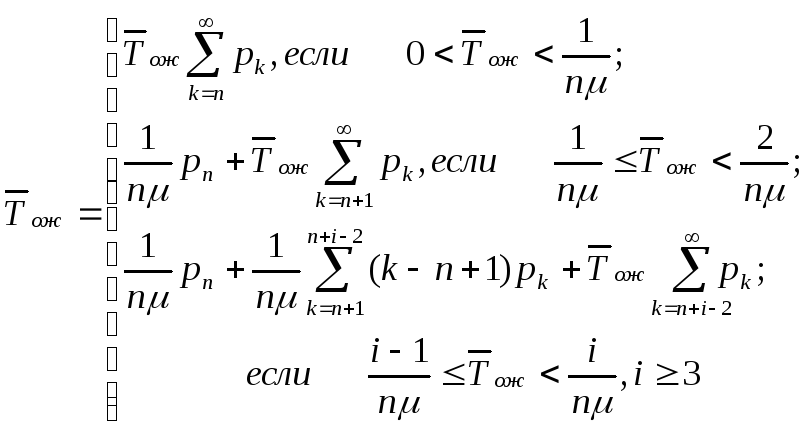Теория массового обслуживания (ТМО) / Конспект лекций по ТМО / TEMA9~1
.DOCМногоканальная СМО без ограничения на длину очереди, но с ограничением на время ожидания
Изучим работу n-канальной
(n
![]() 1) СМО с ожиданием, на вход которой
поступает простейший поток заявок Пвх
с интенсивностью X.
Поток обслуживаний Поб
каждым каналом также предполагается
простейшим с интенсивностью
1) СМО с ожиданием, на вход которой
поступает простейший поток заявок Пвх
с интенсивностью X.
Поток обслуживаний Поб
каждым каналом также предполагается
простейшим с интенсивностью
![]() .
На длину очереди никаких ограничений
не налагается, но время ожидания
каждой заявки в очереди ограничено
случайным сроком Тож
со средним значением
.
На длину очереди никаких ограничений
не налагается, но время ожидания
каждой заявки в очереди ограничено
случайным сроком Тож
со средним значением
![]() ,
после которого заявка покидает
систему необслуженной. Временной
интервал Тож
является непрерывной
случайной величиной, которая может
принимать любое положительное значение
и математическое ожидание которой
,
после которого заявка покидает
систему необслуженной. Временной
интервал Тож
является непрерывной
случайной величиной, которая может
принимать любое положительное значение
и математическое ожидание которой
![]() .
.
Теоретически удобно считать, что заявка из очереди покидает систему под воздействием на нее потока "уходов" Пух с интенсивностью
![]()
Если этот поток пуассоновский, то процесс, протекающий в СМО, будет марковским.
Такие системы часто встречаются на практике. Их иногда называют системами с нетерпеливыми заявками. Для данных систем мы не выделили сначала случай одноканальной СМО, как это делали для ранее рассмотренных систем. Все характеристики для одноканальной СМО могут быть получены из выведенных далее соответствующих " характеристик для n-канальных СМО при п=1.
Занумеруем состояния СМО по числу заявок, находящихся в системе (под обслуживанием и стоящих в очереди):
sk (k = 0, 1, …, n) – k заявок под обслуживанием (k каналов заняты, очереди нет);
sn+r (r = 1, 2, …) – n заявок под обслуживанием (все п каналов заняты) и r заявок в очереди.
Таким образом, СМО может пребывать в одном из бесконечного множества состояний.
Размеченный граф состояний указан на рис. 9.1.
So
S1
Sk
Sn
Sn+1
Sn+r
















 … … … …
… … … …

µ 2µ κµ (κ+1) µ nµ nµ+ω nµ+2ω nµ+rω nµ+(r+1 )ω
Рис.9.1
Из состояния в состояние
слева направо (без перескоков) СМО
переходит под воздействием одного и
того же входящего потока заявок Пвх
с интенсивностью
![]() .
Следовательно, плотности вероятностей
этих переходов:
.
Следовательно, плотности вероятностей
этих переходов:
![]() (9.1)
(9.1)
Переход СМО из состояния
без очереди соседнее слева состояние
sk-1
(k
= 1, …, n),
в котором sk
(k
= 1, …, n)
также не будет очереди, происходит под
воздействием суммарного потока,
слагающегося из k
потоков обслуживании
всех k
занятых каналов,
интенсивность которого, представляющая
собой сумму интенсивностей слагаемых
потоков обслуживании, равна k![]() .
Поэтому под стрелками
справа налево от состояния sn
до состояния sо
проставлены
плотности вероятностей переходов
.
Поэтому под стрелками
справа налево от состояния sn
до состояния sо
проставлены
плотности вероятностей переходов
![]() (9.2)
(9.2)
На систему в состоянии с
очередью sn+r
(r
= 1, 2, …) действует суммарный поток —
результат наложения я потоков обслуживании
и r
потоков уходов. Поэтому
интенсивность суммарного потока
равна сумме интенсивностей слагаемых
потоков
![]() .
Этот суммарный поток порождает переход
СМО справа налево из состояния
sn+r
(r
= 1, 2, …) в соседнее sn+r-1
(r
= 1, 2, …) и, таким образом,
.
Этот суммарный поток порождает переход
СМО справа налево из состояния
sn+r
(r
= 1, 2, …) в соседнее sn+r-1
(r
= 1, 2, …) и, таким образом,
![]() (9.3)
(9.3)
Итак, плотности вероятностей переходов системы по стрелкам справа налево, с учетом равенств (9.2) и (9.3) можно записать в объединенной форме
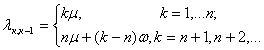 (9.4)
(9.4)
Структура графа (см. рис. 9.1) говорит о том, что процесс, протекающий в СМО, является процессом гибели и размножения.
Подставим равенства (9.1) и (9.4) для k = 1, ..., n + т в формулы (3.21), получим:
 (9.5)
(9.5)
Введем в рассмотрение величину
![]() ,
которую по аналогии с
величиной
,
которую по аналогии с
величиной
![]() можно назвать
приведенной интенсивностью
потока уходов и которая
показывает среднее число уходов из
очереди необслуженных заявок за среднее
время обслуживания одной заявки
можно назвать
приведенной интенсивностью
потока уходов и которая
показывает среднее число уходов из
очереди необслуженных заявок за среднее
время обслуживания одной заявки
![]() .
.
Подставим в равенство (9.5)
вместо отношений
![]() и
и
![]() соответственно
соответственно
![]() и
и
![]() , получим:
, получим:
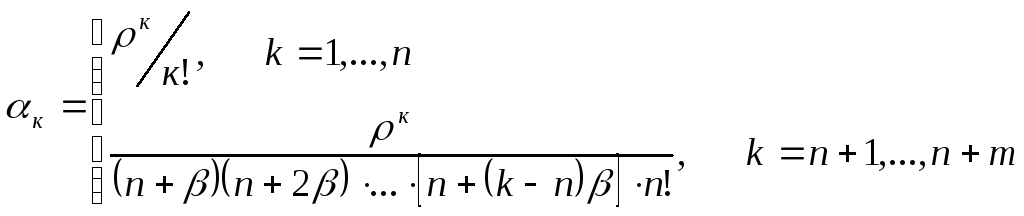 (9.6)
(9.6)
Заменяя в формулах (3.19) и
(3.20) п на
п+т, затем
подставляя в них
![]() по
формуле (9.6) и переходя к пределу при
по
формуле (9.6) и переходя к пределу при
![]() ,
найдем вероятности состояний
,
найдем вероятности состояний
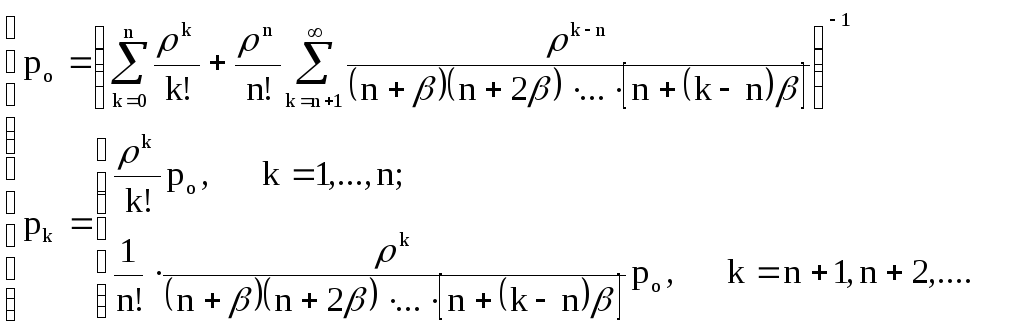 (9.7)
(9.7)
Ряд
![]() ,
(9.8)
,
(9.8)
через который выражается
вероятность
![]() о,
сходится при любых (положительных)
о,
сходится при любых (положительных)
![]() и
и
![]() .
В самом деле, члены
ряда (9.8)
.
В самом деле, члены
ряда (9.8)
![]() положительны, а потому для
доказательства его сходимости можно
применить признак Д'Аламбера. Предел
варианты Д'Аламбера Dk
= ak+1/ak
равен
положительны, а потому для
доказательства его сходимости можно
применить признак Д'Аламбера. Предел
варианты Д'Аламбера Dk
= ak+1/ak
равен
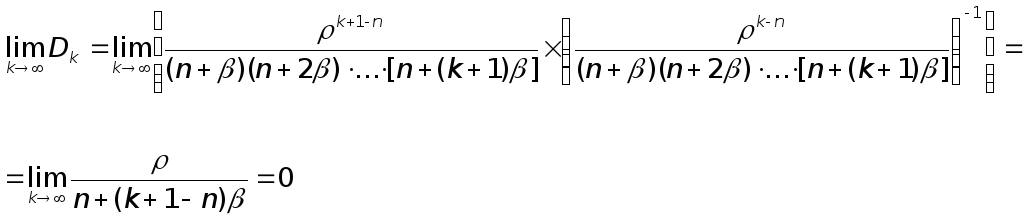
Таким образом,
![]() и
потому ряд (9.8) сходится.
и
потому ряд (9.8) сходится.
Итак, если длина очереди не
ограничена, но имеется ограничение
на время ожидания заявки в очереди (т.е.
заявки "нетерпеливы"), то со временем
(![]() )
устанавливается предельный стационарный
режим и существуют предельные вероятности
состояний (9.7) при любых (положительных)
)
устанавливается предельный стационарный
режим и существуют предельные вероятности
состояний (9.7) при любых (положительных)
![]() и
и
![]() ,
в отличие от случая неограниченной
очереди и неограниченного времени
ожидания заявок в очереди (заявки
терпеливы), в котором,
как было показано в разделе п. 8, предельный
стационарный режим и предельные
вероятности состояний существуют
только при условии
,
в отличие от случая неограниченной
очереди и неограниченного времени
ожидания заявок в очереди (заявки
терпеливы), в котором,
как было показано в разделе п. 8, предельный
стационарный режим и предельные
вероятности состояний существуют
только при условии
![]() ,
т.е. если,
,
т.е. если,
![]() или что тоже,
или что тоже,
![]() .
.
Если в формулах (9.7) перейти
к пределу при
![]() ,
т.е. при
,
т.е. при
![]() или
что то же, при
или
что то же, при
![]() ,
то при условии
,
то при условии
![]() получим формулы (8.3) и (8.4) предельных
вероятностей состояний СМО с
неограниченным временем ожидания
получим формулы (8.3) и (8.4) предельных
вероятностей состояний СМО с
неограниченным временем ожидания
![]() .
Докажем это:
.
Докажем это:
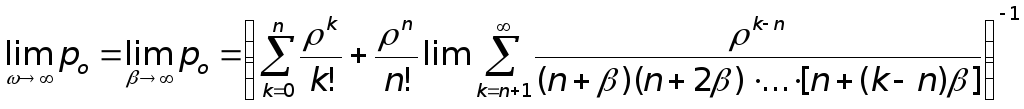 . (9.9)
. (9.9)
Обоснуем, что в ряде (9.8)
возможен почленный переход к пределу.
Члены ряда (9.8) для всех
![]() удовлетворяют
неравенствам
удовлетворяют
неравенствам
 ;
;
(в каждой скобке знаменателя
дроби в левой части неравенства заменили
![]() меньшим числом 0), а ряд
меньшим числом 0), а ряд
![]() ,
в силу условия
,
в силу условия
![]() ,
сходится, поскольку
,
сходится, поскольку
![]() — бесконечно убывающая
геометрическая профессия. Следовательно,
по признаку Вейерштрасса равномерной
сходимости рядов (см., например, [15], с.
430), ряд (9.8) в интервале
— бесконечно убывающая
геометрическая профессия. Следовательно,
по признаку Вейерштрасса равномерной
сходимости рядов (см., например, [15], с.
430), ряд (9.8) в интервале
![]() сходится равномерно относительно
сходится равномерно относительно
![]() .
Тогда (см. например, [Г5], с. 437) в ряде (9.8)
возможен почленный переход к пределу:
.
Тогда (см. например, [Г5], с. 437) в ряде (9.8)
возможен почленный переход к пределу:

Подставив это соотношение в равенство (9.9), получим формулу (8.3):
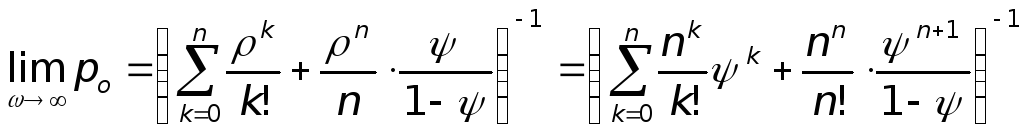
Далее из равенства (9.7):

где po определяется по формуле (8.3).
Если в формулах (9.7) перейти
к пределу при
![]() получим формулы
Эрланга (4.9) для случая n-канальной
системы с отказами.
получим формулы
Эрланга (4.9) для случая n-канальной
системы с отказами.
Так как в рассматриваемой СМО нет ограничений на длину очереди, то каждая заявка, поступившая во входящем потоке, будет принята в систему и в этом смысле отказ со стороны системы заявка не получает. Поэтому для СМО с "нетерпеливыми" заявками вероятность принятия в систему pсис=1, а вероятность отказа принятия в систему ротк=0.
Понятие отказа принятия в систему не следует смешивать с понятием отказа в обслуживании, поскольку, в силу "нетерпеливости", не каждая поступившая (принятая) в систему заявка будет обслужена. Таким образом, имеет смысл говорить о вероятности ухода заявки из очереди pух и вероятности того, что заявка будет обслужена, роб. При этом вероятность роб представляет собой относительную пропускную способность Q и рух=1-роб .
Подсчитаем среднее число заявок в очереди Nоч. Для этого рассмотрим дискретную случайную величину Nоч представляющую собой число заявок в очереди. Случайная величина Nоч может принять любое целое неотрицательное значение, а ее закон распределения имеет вид:
-
Nоч
0
1
2
…
r
…
Р
р
рn+1
рn+2
…
рn+r
…
где р=ро+р1+…+рn. Следовательно,
![]() ,
или, подставив сюда (9.7),
получим
,
или, подставив сюда (9.7),
получим
![]() . (9.10)
. (9.10)
Применяя признак Д'Аламбера, убеждаемся в сходимости ряда в правой части равенства (9.10).
На каждую заявку в очереди
действует поток "уходов" Пух
с интенсивностью
![]() .
На среднюю очередь, состоящую из
.
На среднюю очередь, состоящую из
![]() заявок, будет действовать суммарный
поток, складывающийся из
заявок, будет действовать суммарный
поток, складывающийся из
![]() потоков "уходов" и имеющий
интенсивность
потоков "уходов" и имеющий
интенсивность![]()
![]() .
Значит, из среднего
числа
.
Значит, из среднего
числа
![]() заявок в очереди в среднем будет уходить,
не дождавшись обслуживания,
заявок в очереди в среднем будет уходить,
не дождавшись обслуживания,
![]()
![]() заявок в единицу времени, а оставшиеся
заявки будут обслужены. Следовательно,
среднее число заявок, обслуженных за
единицу времени, т.е. абсолютная пропускная
способность СМО
заявок в единицу времени, а оставшиеся
заявки будут обслужены. Следовательно,
среднее число заявок, обслуженных за
единицу времени, т.е. абсолютная пропускная
способность СМО
![]() . (9.11)
. (9.11)
Тогда по определению относительной пропускной способности
![]() ,
,
где
![]() показывает среднее число уходов из
очереди не обслуженных заявок за среднее
время
показывает среднее число уходов из
очереди не обслуженных заявок за среднее
время
![]() между поступлениями
двух соседних заявок во входящем потоке
Пвх.
между поступлениями
двух соседних заявок во входящем потоке
Пвх.
Среднее число
![]() занятых каналов, или что то же, среднее
число
занятых каналов, или что то же, среднее
число![]() заявок,
находящихся под обслуживанием, можно
получить как отношение абсолютной
пропускной способности А
к производительности
одного канала
заявок,
находящихся под обслуживанием, можно
получить как отношение абсолютной
пропускной способности А
к производительности
одного канала
![]() .
Используя при этом равенство (9.11), будем
иметь:
.
Используя при этом равенство (9.11), будем
иметь:
![]() .
(9.12)
.
(9.12)
Таким образом, чтобы
подсчитать среднее число
![]() занятых каналов по формуле (9.12), нужно
предварительно вычислить
занятых каналов по формуле (9.12), нужно
предварительно вычислить
![]() по формуле (9.10). Однако,
по формуле (9.10). Однако,
![]() можно подсчитать и независимо от
среднего числа заявок в очереди
можно подсчитать и независимо от
среднего числа заявок в очереди
![]() ,
а именно как математическое ожидание
дискретной случайной величины К,
представляющей собой
число занятых каналов, закон распределения
которой имеет вид:
,
а именно как математическое ожидание
дискретной случайной величины К,
представляющей собой
число занятых каналов, закон распределения
которой имеет вид:
-
К
0
1
2
…
n-1
n
Р
po
p1
p2
…
pn-1
p
где p
= pn
+ pn+1
+ pn+2
+ … +
pn+r
+
… . Но так как событие,
состоящее в том, что все п
каналов заняты,
противоположно событию, состоящему
в том, что не все![]() каналов заняты, а
вероятность последнего события равна
(ро + р1 +
р2 + … + рn-1),
то p =
1 - (ро + р1 + р2
+ … + рn-1).
Тогда
каналов заняты, а
вероятность последнего события равна
(ро + р1 +
р2 + … + рn-1),
то p =
1 - (ро + р1 + р2
+ … + рn-1).
Тогда
 .
(9.13)
.
(9.13)
Но тогда из равенства (9.12):
![]() ,
(9.14)
,
(9.14)
где![]() определяется
формулой (9,13).
определяется
формулой (9,13).
Параметры характеристики изученной СМО представлены в табл. 9.1, 9.2
Таблица 9.1 – Параметры многоканальной СМО с ожиданием без ограничения на длину очереди и с ограничением на время ожидания в очереди
|
№ n/n |
Параметры |
Обозначения, значения |
|
1 |
Число каналов обслуживания |
|
|
2 |
Интенсивность входящего простейшего потока Пвх |
( |
|
3 |
Производительность каждого канала – интенсивность простейшего потока обслуживаний Поб каждым каналом (среднее число заявок, обслуживаемых одним каналом за единицу времени при непрерывной его работе) |
( |
|
4 |
Максимальное число мест в очереди |
|
|
5 |
Ограничение на время ожидания заявки в очереди |
Случайное время Тож |
|
6 |
Среднее значение ограничения времени заявки в очереди |
|
|
7 |
Интенсивность простейшего потока уходов из заявки из очереди Пух |
( |
Таблица 9.2 – Характеристики функционирования многоканальной СМО с ожиданием без ограничения на длину очереди и с ограничением на время ожидания в очереди
|
№ n/n |
Предельные характеристики |
Обозначения, формулы |
|
1 |
Показатель (коэффициент) нагрузки СМО (трафик) |
|
|
2 |
Показатель (коэффициент) нагрузки, приходящийся на один канал |
|
|
3 |
Приведённая интенсивность потока «уходов» |
|
|
4 |
Вероятность того, что все n каналов свободны (вероятность простаивания всей системы) |
|
|
5 |
Вероятности состояний |
|
|
6 |
Среднее число заявок в очереди |
|
|
7 |
Среднее число заявок под обслуживанием (т.е. среднее число занятных каналов) |
|
|
8 |
Среднее число заявок в системе |
|
|
9 |
Абсолютная пропускная способность |
|
|
10 |
Относительная пропускная способность |
|
|
11 |
Вероятность того, что заявка будет обслужена |
|
|
12 |
Вероятность ухода заявки из очереди не обслуженной |
рух = 1 - роб |
|
13 |
Среднее время ожидания заявки в очереди |
|
|
14 |
Среднее время пребывания заявки в системе |
|
|
15 |
Среднее время обслуживания одной заявки, относящееся ко всем заявкам – как обслуженным, так и ушедшим из очереди не обслуженными |
|
|
16 |
Среднее время обслуживания одной заявки, относящееся только к обслуженным заявкам |
|
Задания
Тесты
Тест 9.1. Приведенная интенсивность потока уходов равна результату деления интенсивности потока уходов на интенсивность
1) входящего потока
2) потока обслуживании
Тест 9.2. Приведенная интенсивность потока уходов показывает среднее число уходов из очереди необслуженных заявок за среднее время
1) ожидания заявки в очереди
2) обслуживания одной заявки
3) ожидания заявки в системе
Тест 9.3. Для СМО с "нетерпеливыми" заявками абсолютная пропускная способность равна
1) интенсивности входящего потока заявок
2) интенсивности суммарного потока уходов
3) разности интенсивности входящего потока и интенсивности суммарного потока уходов
Тест 9.4. Для n-канальной СМО с "нетерпеливыми" заявками среднее число заявок под обслуживанием
1) равно приведенной интенсивности входящего потока заявок
2) больше приведенной интенсивности входящего потока заявок
3) меньше приведенной интенсивности входящего потока заявок
Тест 9.5. Относительная пропускная способность для п-канальной СМО с "нетерпеливыми" заявками
1) больше единицы
2) меньше единицы
3) равна единице
Тест 9.6. Для n-канальной СМО с "нетерпеливыми" заявками предельный режим функционирования системы существует
1) при любом значении нагрузки системы, приходящейся на один канал
2) при значении нагрузки системы, приходящейся на один канал, меньшем единицы
3) при значении нагрузки системы, приходящейся на один канал, большем единицы
Тест 9.7. Для СМО с "нетерпеливыми" заявками среднее время пребывания заявки в системе равно сумме среднего времени ожидания заявки в очереди и
1) среднего времени обслуживания заявки одним каналом, относящегося только к обслуженным заявкам
2) среднего времени обслуживания заявки одним каналом, относящегося ко всем заявкам — как обслуженным, так и ушедшим из очереди необслуженными