Многоканальная смо с отказами

Изучим работу -канальной СМО с отказами , на вход которой поступает простейший поток заявок с интенсивностью , а время обслуживания каждым каналом одной заявки распределено по показательному закону (3.1). Тогда «поток обслуживаний» каждым каналом будет простейшим с интенсивностью , где - среднее время обслуживания одной заявки одним каналом.

Задача исследования таких СМО впервые возникла в области телефонии и была решена в 1909 г. А.К.Эрлангом.

Состояние системы занумеруем по числу занятых каналов. Для СМО с отказами это означает, что мы нумеруем состояния по числу заявок, находящихся в системе, т.е. под обслуживанием, поскольку каждый канал в любой момент времени либо свободен, либо обслуживает только одну заявку. Таким образом, СМО может находиться только в одном из следующих состояний:

- все каналов свободны,

- занят только один канал, остальные каналов свободны

…

- заняты каналов, остальные каналов свободны,

…

- заняты все каналов.

Граф состояний СМО представлен на рис. 1.

Рис. 1.

Если СМО находится в состоянии , т.е. когда каналов заняты обслуживанием заявок, а остальные каналов свободны, то перескок ее в состояние происходит при поступлении на вход новой заявки. Таким образом, по стрелкам слева направо из любого состояния в соседнее состояние справа систему переводит один и тот же входящий поток заявок с интенсивностью . Следовательно, плотность вероятности перехода из любого -го состояния в -е состояние равна :

(1)

что и проставлено над стрелками слева направо.

Так как по предположению входящий поток простейший, то он является ординарным, т.е. заявки поступают по одной. Поэтому СМО, меняя свои состояния слева направо, не может перескочить через состояние, а переходит только в соседнее справа состояние. По этой причине на графе (рис. 1) отсутствуют стрелки, перескакивающие через состояния слева направо.

Вероятность того, что одновременно, точно в один и тот же момент, освободятся более одного канала, пренебрежимо мала, т.е. такие события практически невозможны. Поэтому на графе нет стрелок, «перескакивающих» через состояние справа налево.

Выясним, каковы интенсивности потоков событий, переводящих СМО по стрелкам справа налево.

На переход занятого канала в состояние свободного действует простейший поток обслуживания с интенсивностью . Но тогда переход СМО в целом из состояния ( в котором каналов заняты, а свободны) в состояние (в котором по сравнению с предыдущим освободился один из каналов) происходит под воздействием суммарного потока обслуживания , представляющего собой результат наложения потоков обслуживания , действующих на каждый из занятых каналов. При этом интенсивность суммарного потока равна сумме интенсивностей слагаемых потоков:

.

Таким образом,

(2)

Проставим найденные плотности вероятностей переходов под стрелками справа налево.

Итак, мы получили размеченный граф состояний -канальной СМО с отказами, из которого видно, что математической моделью процесса, протекающего в этой СМО, является процесс гибели и размножения. Причем, под размножением можно понимать процесс увеличения числа занятых каналов, т.е. переходы СМО из состояния в состояние по стрелкам слева направо, а гибель интерпретировать, как уменьшение числа занятых каналов, т.е. переходы системы по стрелкам справа налево.

Пользуясь общим правилом составления дифференциальных уравнений Колмогорова, можно для вероятностей состояний , составить по графу на рис. 1 следующую систему дифференциальных уравнений:

(3)

которая в случае рассматриваемой СМО называется системой дифференциальных уравнений Эрланга.

Вероятности состояний в любой момент времени удовлетворяет нормировочному условию

. (4)

В начальный момент времени наблюдения за СМО естественно считать, что она находится в состоянии , т.е. все каналы были свободны. Поэтому начальные условия для решения системы (3) выглядят следующим образом:

Решение общих систем дифференциальных уравнений Эрланга в аналитическом виде представляет значительные трудности. На практике такие системы решаются обычно в численном виде на ЭВМ.

При достаточно длительном протекании процесса в рассматриваемой СМО устанавливается стационарный режим, характеризующийся предельными вероятностями состояний СМО:

Которые, как это следует из нормировочного условия (4), удовлетворяют нормировочному условию

. (5)

Для вычисления предельных вероятностей состояний , можно предварительно, решив систему дифференциальных уравнений Эрланга (3), найти вероятности состояний , а затем подсчитать их пределы при

Можно поступить и иначе. Сначала в каждом из дифференциальных уравнений системы Эрланга (3) перейти к пределу при . В результате из системы дифференциальных уравнений (3) можно получить однородную систему линейных алгебраических уравнений, неизвестными в которой как раз и будут предельные вероятности :

Решив эту систему, получим значения .

Но мы найдем предельные вероятности из общих формул (3.19)-(3.21), выведенных для процесса гибели и размножения, подставляя в них значения плотностей вероятностей переходов по формулам (1) и (2).

Из формул (3.21), (1) и (2) получим:

Но можно доопределить по этой же формуле и для , считая, как обычно . Таким образом, из формул (3.19) и (3.20) получаем следующие формулы для вычисления предельных вероятностей, выраженные через и :

(6)

Формулы (3.17) и (3.18) для предельных вероятностей состояний соответственно и одноканальной СМО с отказами, конечно же, следуют из формул (6) при .

Из формул (6) видно, что предельные вероятности зависят от интенсивности входящего потока и интенсивности потока обслуживаний не по отдельности, а от их отношения . Обозначим это отношение через :

. (7)

Величину называют приведенной интенсивностью входящего потока или показателем нагрузки СМО, или трафиком. Так как , то

, (8)

и таким образом приведенная интенсивность входящего потока представляет собой среднее число заявок, поступивших на вход СМО за среднее время обслуживания одной заявки одним каналом, и является показателем нагрузки системы. Единица измерения этого показателя – эрланг.

Подставив выражение (7) в систему (6), получим

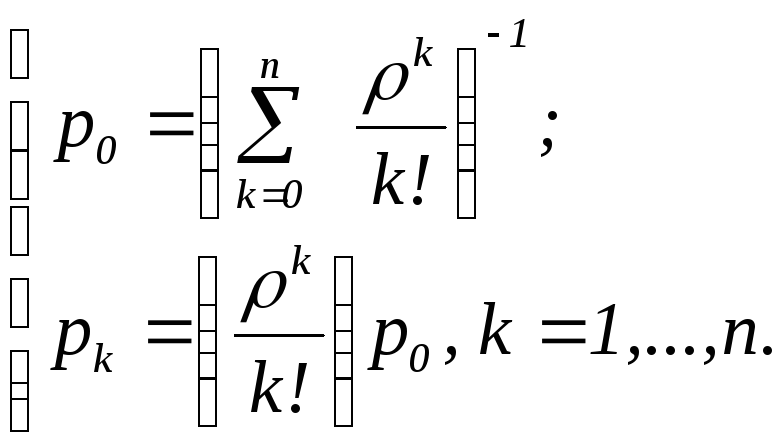(9)

Формулы (9) называются формулами Эрланга. Они выражают предельные вероятности состояний СМО через число каналов и показатель нагрузки . Предельные вероятности состояний можно выразить также и через средний интервал времени между двумя соседними заявками во входящем потоке и среднее время обслуживания одной заявки одним каналом. Для этого достаточно выразить через эти средние времена приведенную интенсивность. Подставим в равенство (8) величину :

. (10)

А теперь, подставив равенство (10) в формулы Эрланга (9), получим формулы:

(11)

Зная все предельные вероятности состояний можно найти предельные характеристики эффективности СМО.

Далее для кратности в названии «предельные характеристики» будем опускать прилагательное «предельные». Вместо «предельная вероятность отказа», «предельная вероятность обслуживания», «предельная относительная пропускная способность» и т.д. будем говорить соответственно «вероятность отказа», «вероятность обслуживания», «относительная пропускная способность» и т.д.

По определению СМО с отказами, заявка получает отказ, если поступает на вход в момент, когда все каналы заняты, т.е. когда СМО находится в состоянии . Поэтому вероятность отказа равна вероятности того, что СМО находится в состоянии . Из второй формулы системы (9) при получаем

(12)

Так как событие, состоящее в том, что пришедшая заявка получит отказ, и событие, состоящее в том, что пришедшая заявка будет принята к обслуживанию, являются противоположными, то их вероятности в сумме дают единицу. А потому вероятность того, что заявка будет обслужена, можно подсчитать по формуле:

(13)

Как было показано ранее, относительная пропускная способность равна вероятности обслуживания:

(14)

Абсолютная пропускная способность

(15)

Интенсивность выходящего потока обслуженных заявок

(16)

Для многоканальной СМО с отказами одной из важных характеристик ее эффективности является среднее число занятых каналов , или что то же, среднее число заявок под обслуживанием , которое для СМО с отказами совпадает со средним числом заявок, находящихся в системе . Величину можно подсчитать следующим образом: так как абсолютная пропускная способность есть среднее число заявок, обслуживаемых СМО в единицу времени, а один занятый канал обслуживает в среднем за единицу времени заявок, то среднее число занятых каналов будет равно отношению или, применяя (15) и (7), получим

. (17)

К формуле (17) можно было прийти и другим путем, а именно, подсчитать величину как математическое ожидание дискретной случайной величины , представляющей собой число занятых каналов. Случайная величина может принимать значения с вероятностями соответственно . Тогда, используя известную из теории вероятностей формулу для математического ожидания дискретной случайной величины формулы предельных вероятностей (9) и нормировочное условие (5), получим:

Наконец, выведем формулу для вычисления среднего времени обслуживания заявки , относящегося ко всем заявкам – как к обслуженным, так и получившим отказ. Среднее время не следует путать со средним временем обслуживания заявки , которое относится только к обслуженным заявкам. Для рассматриваемых СМО с отказами среднее время совпадает со средним временем пребывания заявки в системе .

Рассмотрим гипотез , состоящих в том, что система находится в состояниях соответственно. Вероятности этих гипотез равны . Если заявка поступает в СМО при гипотезе , т.е. когда СМО находится в состоянии , то заявка немедленно попадает под обслуживание, и потому условное математическое ожидание непрерывной случайной величины - времени обслуживания при гипотезе равно среднему времени обслуживания . Если же заявка приходит в СМО при гипотезе , т.е. когда система находится в состоянии , в котором все каналов заняты, то заявка получает отказ, и потому =0. Следовательно, по формуле полного математического ожидания:

Но в силу нормировочного условия имеем

,

и, следовательно,

(18)

Отсюда, используя формулы (7) и (7), получаем формулу Литтла:

или .

Формула Литтла показывает, что среднее время пребывания заявки в СМО равно среднему числу заявок в системе , деленному на интенсивность входящего потока заявок, или, другими словами, среднее время пребывания заявки в СМО прямо пропорционально среднему числу заявок в системе с коэффициентом прямой пропорциональности, равным обратной величине интенсивности входящего потока заявок.

Отметим, что формулы (13), (13), (14), (15), (16) и (18) при превращаются соответственно в формулы (3.28), (3.24), (3.25), (3.26), (3.27) и (3.29).

Формулу (17) при

(19)

можно интерпретировать как среднее число занятых каналов или заявок, находящихся в системе одноканальной СМО. Подставляя в (19) выражения по формуле (7) и по формуле (3.24), получим , что в сравнении с (3.28) дает , т.е. среднее число занятых каналов многоканальной СМО совпадает по значению с вероятностью отказа.

Для удобства пользования сведем исходные параметры СМО и выведенные предельные характеристики эффективности ее функционирования в табл.1 и 2.

Таблица 1