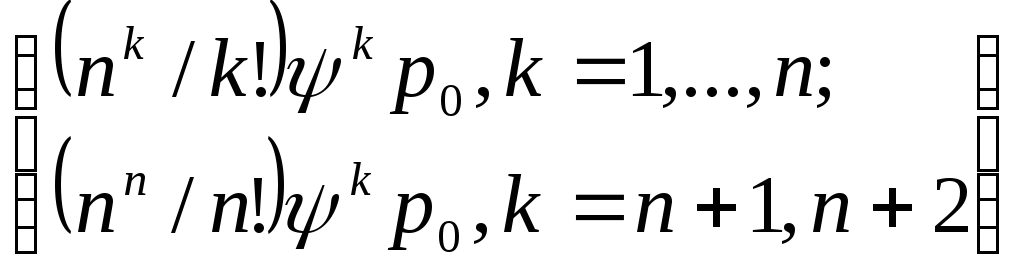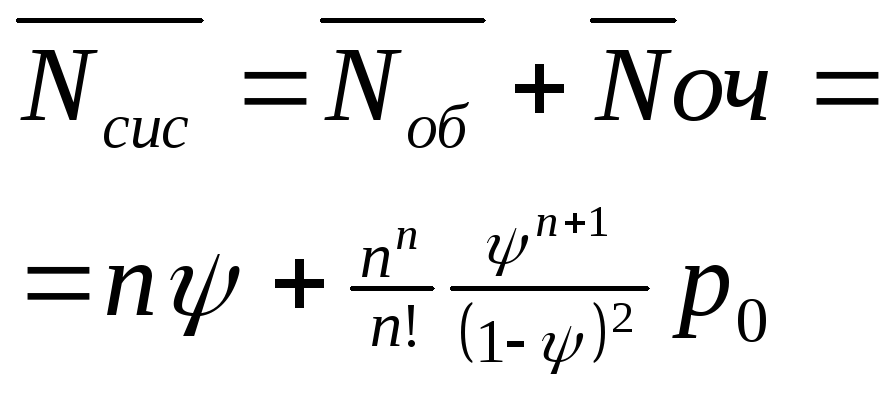Теория массового обслуживания (ТМО) / Конспект лекций по ТМО / TEMA8~1

Многоканальная СМО с ожиданием

Рассмотрим СМО, состоящую из каналов обслужива­ния, с ожиданием и без ограничения на длину очереди. Заявка, поступившая в СМО в момент, когда все и каналов заняты, становится в очередь и ожидает своего обслуживания. Любая пришедшая заявка будет обслужена. Поток заявок П_вх и поток обслуживании каждым каналом П_0б - простейшие с интенсив­ностью соответственно и. Такая система может находиться в одном из бесконечного множества состояний.

S_k (k = О, 1, ..., n) — k каналов заняты и очереди нет,

S_n+r (г = 1, 2, ...) — все n каналов заняты и в очереди r зая­вок.

Аналогично случаю n-канальной СМО с ожиданием и огра­ничением на длину очереди в разделе 7 получаем размеченный бесконечный граф рассматриваемой системы, представленный на рис. 8.1.

Предельный (стационарный) режим протекающего в СМО марковского случайного процесса будет существовать при усло­вии, что показатель нагрузки, приходящейся на один канал,

(8.1)

Так как =p/n, а р =. то условие (8.1) означает, что < n, т.е. интенсивность n обслуживания всех n каналов вы­ше интенсивности входящего потока. Если условие (8.1) не выполняется, то очередь заявок в системе с течением времени будет неограниченно расти.

Для вычисления вероятности p₀ можно перейти к пределу при m в равенстве (7.4). Получим

(8.2)

где — сумма бесконечной геометрической прогрессии

с первым членом ⁿ⁺¹ и знаменателем , сходящейся только при выполнении условия (8.1). В противном случае

и, следовательно, p₀ = 0, чего быть не может,

поскольку в этом случае, по формулам (7.6), р_k = О, k = 1,2, ..., т.е. вероятности всех состояний будут равны нулю, в то время как они должны удовлетворять нормировочному условию

Итак, при условии (8.1),

и из (8. 2) получим:

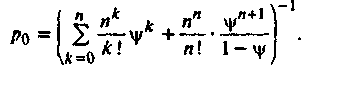
Остальные вероятности состояний найдем из формул (7.6) при m:

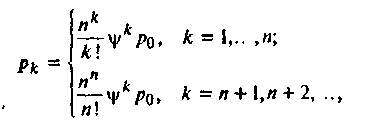
где р_о определяется формулой (8.3).

Отметим, что найденные вероятности состояний (8.3) и (8.4) удовлетворяют нормировочному условию p₀+p₁+…=1

В самом деле,

Для нахождения вероятности отказа заявке перейдем в ра­венстве (7.7) к пределу при m, в результате получим:

(8.5)

что соответствует действительности, поскольку ни одна из по­ступивших в СМО заявок не получает отказа.

Подстанавливая (8.5) в (7.8), найдем вероятность того, что пришедшая заявка будет принята в систему,

(8.6)

Действительно, пришедшая заявка либо сразу попадает под обслуживание, если свободен хотя бы один из каналов, либо становится в очередь, если все n каналов заняты.

Из равенства (7.9) с учетом равенства (8.6) получим, что от­носительная пропускная способность системы

(8.7)

Это отвечает рассматриваемой ситуации, так как все посту­пившие заявки будут обслужены.

Подставив значение (8.7) в равенство А = Q , получим, что абсолютная пропускная способность

(8.8)

т.е. среднее число заявок, поступающих в единицу времени, будет обслужено системой.

Из формул (7.10) и (8.8) с учетом равенства р = получа­ем, что среднее число К занятых каналов, или, другими сло­вами, среднее число заявок, находящихся под обслуживанием,

K = N_об = p (8.9)

Переходя к пределу при m+, в верхней строке формулы (7.12), найдем среднее число заявок, находящихся в очереди:

(8.10)

Подставим соотношения (8.9) и (8.10) в равенство (7.13), получим среднее число заявок, находящихся в системе:

(8.13)

Из формул (7.14) и (8.10) найдем среднее время ожидания заявки в очереди

(8.12)

Наконец, подставив равенство (8.11) в формулу (7.17), полу­чим среднее время пребывания заявки в системе:

(8.13)

Так как в случае рассматриваемой СМО каждая поступив­шая заявка будет обслужена, то среднее время обслуживания

одной заявки, относящееся ко всем заявкам T _об, представляет собой среднее время обслуживания одной заявки, относящееся только к обслуженным заявкам Т _Об . Таким образом,

Легко убедиться в том, что при n = 1 формулы (8.3) и (8.4) превращаются в формулу (6.1) соответственно для k = 0 и k 1, а формулы (8.10), (8.11), (8.12) и (8.13)- соответственно в формулы (6.2), (6.4), (6.5) и (6.6).

В заключение приведем табл. 8.1 и 8.2 параметров и пре­дельных характеристик исследованной в этом разделе СМО.

Таблица 8.1

Параметры многоканальной СМО с ожиданием

№ п/п	Параметры	Обозначения, значения
1	Число каналов обслуживания	n1
2	Интенсивность входящего простей­шего потока заявок Пвх	in Пвх = = const (. не зависит от времени)
3	Производительность каждого кана­ла — интенсивность простейшего потока обслуживании Пoб каждым каналом (среднее число заявок, об­служиваемых одним каналом за еди­ницу времени при непрерывной его работе)	in Поб = = const ( не зависит от времени)
4	Максимальная длина очереди — максимальное число мест в очереди	m= +
5	Соотношение между n, и	< n,

Таблица 8.2

Характеристики функционирования

многоканальной СМО с ожиданием

№ п/п	Предельные характеристики	Обозначения, формулы
1	Показатель (коэффициент) нагрузки СМО (трафик)	р = /
2	Показатель (коэффици­ент) нагрузки, приходя­щейся на один канал	= (р/n) <1
3	Вероятность того, что все каналы свободны (вероят­ность простаивания всей системы)	p0 =
4	Вероятности состояний	pk=
5	Вероятность отказа	pотк =0
6	Вероятность того, что заявка будет принята в СМО	pсис = 1

Окончание табл. 8.2

№ п/п	Предельные характеристики	Обозначения, формулы
7	Относительная пропускная способность	Q= 1
8	Абсолютная пропускная способность	A =
9	Среднее число занятых каналов — среднее число заявок, находящихся под обслуживанием
10	Среднее число заявок, находящихся в очереди
11	Среднее число заявок, на­ходящихся в СМО (как в очереди, так и под обслуживанием)
12	Среднее время ожидания заявки в очереди
13	Среднее время пребывания заявки в системе
14	Среднее время обслужива­ния одной заявки