Теория массового обслуживания (ТМО) / Конспект лекций по ТМО / TEMA7~1

Многоканальная СМО

с ожиданием и ограничением

на длину очереди

В этом параграфе рассмотрим n-канальную (n) СМО с ожиданием, максимальное число мест в очереди которой равно . Пусть на вход СМО поступает простейший поток заявок П_вх с интенсивностью . Поток обслуживании Поб каждым ка­налом также простейший с интенсивностью .

Так как указанные потоки стационарны, то и не изме­няются с течением времени. Заявка, поступившая в СМО в момент, когда в очереди уже стоят т заявок, получает отказ и покидает систему.

Занумеруем состояния системы по числу заявок, находя­щихся в СМО, как в очереди, так и под обслуживанием:

S0 - в СМО нет заявок, т.е. все п каналов свободны;

S1 - в СМО одна заявка, т.е. занят один канал, остальные свободны;

Sk - в СМО k(<n) заявок, т.е. заняты k каналов, а ос­тальные n-k свободны;

Sn - в СМО п заявок, т.е. все n каналов заняты, очереди

нет;

Sn+1 - в СМО n+1 заявка, т.е. все п каналов заняты и одна

заявка — в очереди;

Sn+r - в СМО n+r заявок, т.е. все я каналов заняты и в очереди стоят г заявок;

Sn+m - в СМО n+m заявок, т.е. все я каналов заняты и т

заявок стоят в очереди.

Таким образом, данная СМО может находиться в одном из n+т+ 1 состояний. В состояниях So,S1,…,Sn очереди нет. Разме­ченный граф состояний рассматриваемой системы изображен на рис. 7.1.

Переходы СМО из состояния в состояние по стрелкам направо происходят под воздействием одного и того же входящего потока Пвх, заявок с интенсивностью . Поэтому плотности вероятностей переходов

(7.1)

Если система находится в состоянии, в котором занято k () каналов, то переход ее в левое соседнее состояние порождается потоком, представляющим собой сумму k потоков обслуживании. Поэтому интенсивность этого суммарного пото­ка будет равна . Таким образом, плотности вероятностей переходов СМО по стрелкам справа налево

если k=1,…, n;

если k=n+1,…,n+m (7.2)

Из графа состояний видно, что процесс, протекающий в СМО, является процессом гибели и размножения с конечным числом состояний. Поэтому со временем установится предель­ный режим его протекания, и существуют предельные вероят­ности состояний pk, k=0,1…,n+m, которые можно найти из формул (3.19)—(3.21), заменяя в них п на п+т и подставляя (7.1) и (7.2).

Для к = 1, .... п подставим формулы (7.1) и (7.2) в формулу (3.21), используя показатель нагрузки, получим:

; k=1,…,n

Для k=n+1 из формул (3.21), (7.1) и (7.2) будем иметь:

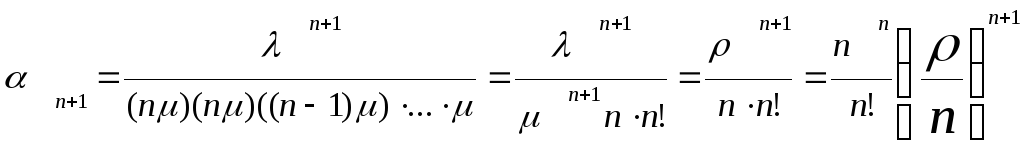
Аналогично

Итак,

,…,

=1,…,n;

=n+1,…,n+m

Введем в рассмотрение величину , представляющую

-собой показатель нагрузки, приходящейся на один канал, получим

, k=1,…,n;

, k=n+1,…,n+m

Тогда из выражения (3.19):

(7.4)

Вторая сумма в правой части равенства (7,4) есть сумма т членов геометрической прогрессии с первым членом и знаменателем . Если, то по формуле суммы т членов геометрической прогрессии

Если же , то

Таким образом, (7.4) примет вид

, если

, если (7.5)

Теперь мы можем найти и остальные предельные вероятно­сти состояний, подставив равенство (7.3) в формулу (3.20):

, k=1,…,n;

, k=n+1,…, n+m (7.6)

где определяется по формуле (7.5).

Используя найденные предельные вероятности состояний, выведем формулы для некоторых характеристик эффективности функционирования рассматриваемой СМО.

Заявка, поступившая в момент, когда заняты все я каналов и все т мест в очереди, т.е. когда СМО находится в состоянии получает отказ. Поэтому вероятность отказа есть вероят­ность того, что СМО находится в состоянии . Следователь­но, из равенства (7.6) при k=п+т получаем:

(7.7)

Поскольку события отказа заявке и приема ее в СМО явля­ются противоположными, то вероятность принятия в систему пришедшей заявки

(7.8)

Относительная пропускная способность Q совпадает с веро­ятностью :

(7.9)

Тогда абсолютная пропускная способность:

Выведем формулу для среднего числа занятых каналов, или что то же, для среднего числа заявок, находящихся под обслуживанием. Так как каждый занятый канал обслужива­ет в среднем заявок в единицу времени, а вся система обслу­живает в среднем А заявок в единицу времени, то

(7.10)

Для вычисления среднего числа заявок, находящихся в очереди, рассмотрим дискретную случайную величину -число заявок в очереди.

Очевидно, что закон распределения этой случайной вели-: чины будет иметь вид:

	0	1	2	• ••	т
P				...

Здесь р = ро + р1 +...+ рn. Поясним, что случайная величи­на принимает значение 0 с вероятностью />, равной сумме вероятностей ро + р1 +...+ рn ,поскольку событие, состоящее в том, что в очереди нет ни одной заявки, является объединени­ем событий, состоящих в том, что СМО находится в каждом из состояний до. Исходя из этого закона распределения, среднее число подсчитаем как математическое ожидание случайной величины , используя формулы (7.6):

(7.11)

В сумме правой части этого равенства произведем замену индекса суммирования: l=k-n. Тогда k=l+n, l = 1 при k=n+1 и l=m при k=n+m. В результате получим:

Пользуясь формулой (5.12) при замене в ней на \|/ 1 и формулой суммы т членов арифметической прогрессии , найдем для окончательное выражение:

(7.12)

Зная среднее число заявок, находящихся под обслуживанием, и среднее число заявок, стоящих в очереди, можно найти среднее число заявок, находящихся в системе:

= + (7.13)

Теперь подсчитаем среднее время ожидания заявки в очереди. Рассмотрим п + т + 1 несовместных гипотез Hk, k=0,1,…,n+m, состоящих в том, что СМО находится соот­ветственно в состоянии ,k=0,1,…,n+m. Тогда вероятно­сти этих гипотез р(Нk)=, k=0,1,…, п + т.

Если заявка поступит в СМО при одной из гипотез , т.е. когда СМО находится в одном из состоя­ний , в каждом из которых не все каналы заняты, то она немедленно попадает под обслуживание свобод­ного канала и ей не придется стоять в очереди. Поэтому услов­ное математическое ожидание случайной величины Т_оч - времени ожидания заявки в очереди при гипотезах представляющее собой среднее время ожида­ния в очереди заявки, поступившей в СМО в момент, когда последняя находилась в состоянии равно нулю: Если заявка поступит в систему при гипотезе Нn , т.е. когда СМО находится в состоянии sn, в котором все n каналов заняты, но очереди нет, то заявке придется ждать освобождения одного из п каналов, которое произойдет под воздействием суммарного по­тока, слагающегося из n потоков обслуживании, каждый из кото­рых имеет интенсивность . Поэтому интенсивность этого сум­марного потока будет равна , а условное математическое ожида­ние случайной величины Tоч при гипотезе Нn совпа­дающее со средним временем ожидания в очереди заявки, посту­пившей в СМО, когда последняя находилась в состоянии sn, равно ,т.е. M[Tоч|Hn] = .

Если заявка поступит в СМО при гипотезе Нn+1, т.е. когда система пребывает в состоянии 5„+\, в котором все я каналов заняты и в очереди одна заявка, то поступившей заявке при­дется в очереди, в среднем ждать время, равное , склады­вающееся из среднего времени 1/(яц) освобождения одного из каналов, под обслуживание которого попадает заявка, стоящая в очереди впереди, и среднего времени следующего ос­вобождения одного из каналов. Поэтому

И так далее. Если заявка поступит в систему при гипотезе , то М[Т_оч|Нn+m+1 ]=.

Наконец, если заявка поступит в СМО при гипотезе Hn+m, т.е. когда система находится в состоянии sn+m, в котором все n каналов заняты и в очереди стоят т заявок, то она получает отказ и покидает систему. Следовательно, M[Tоч|Hn+m] = 0.

Таким образом, по формуле полного математического ожи­дания ([9], с. 77)

Подставим сюда выражения вероятностей состояний по формулам (7.6), получим:

Сделав в сумме справа замену индекса суммирования l= k + 1 и затем заменив l на k, будем иметь:

Но тогда по формуле (7.11):

(7.14)

Таким образом, как и в случае одноканальный СМО с ожи­данием и с ограничением на длину очереди, получили формулу Литтла, показывающую, что среднее время ожидания заявки в очереди Т_оч прямо пропорционально среднему числу заявок в очереди N_оч с коэффициентом .

Подставив равенство (7.12) в формулу (7.14), можно получить другое выражение для :

Аналогично тому, как это было сделано в разделе 5 для одноканальной СМО, можно вывести выражение для среднего времени пребывания заявки в системе (см. формулу (5. 26)):

(7.15)

где— среднее время обслуживания одной заявки, относя­щееся ко всем заявкам - обслуженным и "отказникам":

откуда с учетом (7.10) получаем формулу Литтла:

(7.16)

Подставим равенства (7.14) и (7.16) в формулу (7.15) и с учетом формулы (7.13) получим еще одну формулу Литтла:

(7.17)

связывающую среднее время пребывания заявки в системе со средним числом заявок в системе .

Нетрудно убедиться в том, что при n = 1 формулы (7.5) и (7.6) превращаются в формулы (5.5) соответственно для ро и рk (k= 1,…, т + 1), а формулы (7.7), (7.8),(7.9), (7.10), (7.12), (7.13), (7.14), (7.16) и (7.17)- соответственно в формулы (5.7), (5.8), (5.9), (5.19), (5.17), (5.20), (5.23), (5.25) и (5.27) для одноканальной СМО с ожиданием и ограничением на длину очереди.

Сведем параметры и полученные характеристики функцио­нирования рассмотренной СМО в табл. 7.1 и 7.2.

Таблица 7.1

Параметры многоканальной СМО с ожиданием и ограничением на длину очереди

N&n/n	Параметры	Обозначения, значения
1	Число каналов обслуживания
2	Интенсивность входящего простейшего потока заявок Пвх.	In Пвх==const ( не зависит от времени
3	Производительность каждого кана- ла — интенсивность простейшего потока "обслуживании" Поб каждым каналом (среднее число заявок, об- служиваемых одним каналом за еди- ницу времени при непрерывной его работе)	in Поб==const ( не зависит ни от времени, ни от канала)
4	Максимальная длина очереди — максимальное число мест в очереди

Таблица 7.2

Характеристики функционирования многоканальной СМО с ожиданием и ограничением на длину очереди

№ n/n	Предельные характеристики	Обозначения, формулы
1	Показатель (коэффициент) нагрузки СМО(трафик)
2	Показатель(коэффициент) нагрузки, приходящейся на один канал
3	Вероятность того, что все каналы свободны(вероятность простаивания всей системы)
4	Вероятность состояний
5	Вероятность отказа заявке
6	Вероятность того, что заявка будет принята в СМО
7	Относительная пропускная способность СМО
8	Абсолютная пропускная способность СМО
9	Среднее число занятых каналов(т.е. среднее число заявок, находящихся под обслуживанием )
10	Среднее число заявок, находящихся в очереди
11	Среднее число заявок, находящихся в СМО (как в очереди, так и под обслуживанием)
12	Среднее время ожидания заявки в очереди
13	Среднее время пребывания заявки в системе
14	Среднее время обслуживания одной заявки, относящееся ко всем заявкам – как обслуженным, так и получившим отказ.